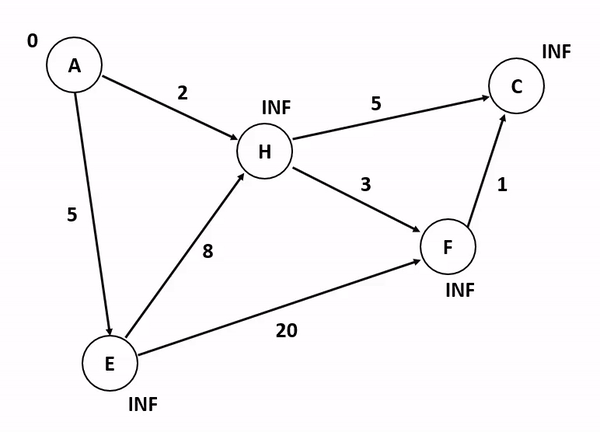
다익스트라(dijkstra)란?
💡 가중치가 있는 그래프에서 특정 노드에서 다른 모든 노드까지의 최단 경로를 구하는 알고리즘이다.
음의 가중치가 없는 그래프에서만 작동한다.
작동 방식
- 초기화, 시작노드 선택
- 인접 노드 거리 갱신
- 가장 가까운 노드 선택
- 2, 3번을 반복하면서 큐에 남은 노드가 없을 때까지 반복
언제 쓸까?
💡 주로 최소 비용을 찾는 문제에서 쓰이며, 시간복잡도가 O(ElogV)이기에 정점 혹은 간선이 10만개로 큰 경우 다익스트라 문제이다.
어떻게 풀까?
- 우선순위 큐(heapq) 기반
큰 그래프에도 효율적으로 작동함
# 우선순위 큐
import heapq
def dijkstra(graph, start):
# 최단 거리를 저장할 딕셔너리
distances = {node: float('inf') for node in graph}
distances[start] = 0
# 우선순위 큐 (최소 힙) 초기화
priority_queue = [(0, start)]
while priority_queue:
current_distance, current_node = heapq.heappop(priority_queue)
# 이미 처리된 노드라면 무시
if current_distance > distances[current_node]:
continue
# 현재 노드와 연결된 다른 인접 노드들을 확인
for neighbor, weight in graph[current_node]:
distance = current_distance + weight
# 계산된 거리가 기존 거리보다 짧으면 갱신
if distance < distances[neighbor]:
distances[neighbor] = distance
heapq.heappush(priority_queue, (distance, neighbor))
return distances- 덱(deque)을 사용하는 0-1 BFS
간선 가중치가 0이나 1만 있을 경우 BFS를 통해 더 효율적으로 해결할 수 있음
from collections import deque
def zero_one_bfs(graph, start):
n = len(graph)
distance = [float('inf')] * n
distance[start] = 0
dq = deque([start])
while dq:
u = dq.popleft()
for v, w in graph[u]:
if distance[u] + w < distance[v]:
distance[v] = distance[u] + w
if w == 0:
dq.appendleft(v)
else:
dq.append(v)
return distance1. 특정 거리의 도시 찾기
문제
어떤 나라에는 1번부터 N번까지의 도시와 M개의 단방향 도로가 존재한다. 모든 도로의 거리는 1이다.
이 때 특정한 도시 X로부터 출발하여 도달할 수 있는 모든 도시 중에서, 최단 거리가 정확히 K인 모든 도시들의 번호를 출력하는 프로그램을 작성하시오. 또한 출발 도시 X에서 출발 도시 X로 가는 최단 거리는 항상 0이라고 가정한다.
예를 들어 N=4, K=2, X=1일 때 다음과 같이 그래프가 구성되어 있다고 가정하자.
이 때 1번 도시에서 출발하여 도달할 수 있는 도시 중에서, 최단 거리가 2인 도시는 4번 도시 뿐이다. 2번과 3번 도시의 경우, 최단 거리가 1이기 때문에 출력하지 않는다.
입력
첫째 줄에 도시의 개수 N, 도로의 개수 M, 거리 정보 K, 출발 도시의 번호 X가 주어진다. (2 ≤ N ≤ 300,000, 1 ≤ M ≤ 1,000,000, 1 ≤ K ≤ 300,000, 1 ≤ X ≤ N) 둘째 줄부터 M개의 줄에 걸쳐서 두 개의 자연수 A, B가 공백을 기준으로 구분되어 주어진다. 이는 A번 도시에서 B번 도시로 이동하는 단방향 도로가 존재한다는 의미다. (1 ≤ A, B ≤ N) 단, A와 B는 서로 다른 자연수이다.
출력
X로부터 출발하여 도달할 수 있는 도시 중에서, 최단 거리가 K인 모든 도시의 번호를 한 줄에 하나씩 오름차순으로 출력한다.
이 때 도달할 수 있는 도시 중에서, 최단 거리가 K인 도시가 하나도 존재하지 않으면 -1을 출력한다.
예제 입력
4 4 2 1
1 2
1 3
2 3
2 4예제 출력
4문제 풀이
import sys, heapq
input = sys.stdin.readline
N, M, K, X = map(int, input().split())
graph = {}
def dijkstra(graph, start):
distances = {node: float('inf') for node in range(1, N+1)}
distances[start] = 0
priority_queue = [(0, start)]
while priority_queue:
current_distance, current_node = heapq.heappop(priority_queue)
if current_distance > distances[current_node]:
continue
for neighbor in graph.get(current_node, []):
distance = current_distance + 1
if distance < distances[neighbor]:
distances[neighbor] = distance
heapq.heappush(priority_queue, (distance, neighbor))
return distances
for i in range(M):
a, b = map(int, input().split())
if a in graph:
graph[a].append(b)
else:
graph[a] = [b]
distances = dijkstra(graph, X)
result = []
for city, dist in distances.items():
if dist == K:
result.append(city)
for m in sorted(result):
print(m)
if result == []:
print(-1) 다익스트라를 쓰는 것 까지는 똑같지만 모든 노드의 가중치가 1인 점을 의식해서 조금 수정해줘야 한다.
출발 도시를 주고 최단거리가 K인 노드만 찾으면 되기 때문에 dijkstra 함수로 반환한 최단거리 딕셔너리에서 거리가 K인 값만 모아서 오름차순으로 출력하면 끝이다.
2. 집 구하기
문제
안양에 사는 상혁이는 4년간의 통학에 지쳐 서울에 집을 구하려고 한다. 상혁이가 원하는 집은 세가지 조건이 있다.
- 맥세권 : 맥세권인 집은 맥도날드와 집 사이의 최단거리가 x이하인 집이다.
- 스세권 : 스세권인 집은 스타벅스와 집 사이의 최단거리가 y이하인 집이다.
- 맥세권과 스세권을 만족하는 집 중 최단거리의 합이 최소인 집
통학 때문에 스트레스를 많이 받은 상혁이는 집을 선택하는 데 어려움을 겪고 있다. 똑똑한 여러분이 상혁이 대신 이 문제를 해결해 주자. 이사 갈 지역의 지도가 그래프로 주어지고 맥도날드와 스타벅스의 위치가 정점 번호로 주어질 때 상혁이가 원하는 집의 최단거리의 합을 출력하는 프로그램을 작성하시오. (맥도날드와 스타벅스가 아닌 정점에는 모두 집이 있다.)

위의 예제 지도에서 사각형은 맥도날드를, 별은 스타벅스가 위치한 정점을 나타낸다. 각 원은 집이 있는 정점을 낸다. x가 6이고 y가 4일 때 가능한 집의 정점은 6이다. 맥도날드까지의 최단거리가 2, 스타벅스까지의 최단거리가 4로 총 합이 6이 되기 때문이다. 정점 7은 맥세권이면서 스세권이지만 맥도날드까지의 최단거리가 6, 스타벅스까지의 최단거리가 2로 총 합이 8로써 정점 6의 값보다 크므로 답이 아니다. 그 외의 정점 2, 3, 4는 맥세권이면서 스세권인 조건을 충족하지 못하므로 답이 될 수 없다.
입력
첫줄에는 정점의 개수 V(3 ≤ V ≤ 10,000)와 도로의 개수 E(0 ≤ E ≤ 300,000)가 주어진다. 그 다음 E줄에 걸쳐 각 도로를 나타내는 세 개의 정수 (u,v,w)가 순서대로 주어진다. 이는 u와 v(1 ≤ u,v ≤ V)사이에 가중치가 w(1 ≤ w < 10,000)인 도로가 존재한다는 뜻이다. u와 v는 서로 다르며 다른 두 정점 사이에는 여러 개의 간선이 존재할 수도 있음에 유의한다. E+2번째 줄에는 맥도날드의 수 M(1 ≤ M ≤ V-2) 맥세권일 조건 x(1 ≤ x ≤ 100,000,000)가 주어지고 그 다음 줄에 M개의 맥도날드 정점 번호가 주어진다. E+4번째 줄에는 스타벅스의 수 S(1 ≤ S ≤ V-2)와 스세권일 조건 y(1 ≤ y ≤ 100,000,000)가 주어지고 그 다음 줄에 S개의 스타벅스 정점 번호가 주어진다.
- 맥도날드나 스타벅스가 위치한 정점에는 집이 없다.
- 한 정점에 맥도날드와 스타벅스가 같이 위치할 수 있다.
- 집이 있는(= 맥도날드나 스타벅스가 위치하지 않은) 정점이 하나 이상 존재한다.
출력
상혁이가 원하는 집의 맥도날드까지의 최단거리와 스타벅스까지의 최단거리 합을 출력한다. 만일 원하는 집이 존재하지 않으면 -1을 출력한다.
예제 입력 1
8 11
1 2 2
1 4 1
2 4 2
2 3 1
2 7 8
3 7 3
4 5 2
4 6 1
6 7 6
6 8 4
7 8 2
2 6
1 5
1 4
8
예제 출력 1
6문제 풀이
import sys, heapq
from collections import defaultdict
input = sys.stdin.readline
V, E = map(int, input().split())
graph = defaultdict(list)
for i in range(E):
u, v, w = map(int, input().split())
graph[u].append((v, w))
graph[v].append((u, w))
M, x = map(int, input().split())
M_list = list(map(int, input().split()))
S, y = map(int, input().split())
S_list = list(map(int, input().split()))
def dijkstra(starts):
distances = {node: float('inf') for node in range(1, V+1)}
priority_queue = []
for s in starts:
distances[s] = 0
heapq.heappush(priority_queue, (0, s))
while priority_queue:
curr_dist, curr_node = heapq.heappop(priority_queue)
if curr_dist > distances[curr_node]:
continue
for neighbor, weight in graph[curr_node]:
distance = curr_dist + weight
if distance < distances[neighbor]:
distances[neighbor] = distance
heapq.heappush(priority_queue, (distance, neighbor))
return distances
result = []
mac = dijkstra(M_list)
star = dijkstra(S_list)
for i in range(1, V+1):
if i in M_list or i in S_list:
continue
if mac[i] <= x and star[i] <= y:
result.append(mac[i] + star[i])
if result:
print(min(result))
else:
print(-1)하나하나 다익스트라를 돌리면 너무 시간이 오래 걸린다.
각 지점마다 역세권과 스세권을 알면 되므로 이런 경우에는 멀티 소스 다익스트라 를 쓰면 된다.
멀티 소스 다익스트라는 각 노드마다 한 시작점과의 최단거리가 아닌 특정 시작점들과의 최단거리 중 최솟값을 구하는 알고리즘이다.
이 알고리즘을 통해 맥도날드 지점 리스트를 넣어서 돌리기만 하면 모든 지점마다 가장 가까운 맥도날드와의 최단거리가 저장될 것이다.
기존 다익스트라 코드에서 시작부분만 이런식으로 변경하면 된다.
priority_queue = []
for s in starts:
distances[s] = 0
heapq.heappush(priority_queue, (0, s))위 알고리즘을 사용할 경우 모든 지점을 조사하는게 아닌 맥세권과 스세권 2번만 돌리면 되므로 실행시간이 대폭 줄어든다.
맥세권과 스세권에 해당하는 지점을 찾고 결과에 포함시키면서 최종적으로 결과값들의 최솟값을 출력하면 된다.
오답 노트
import sys, heapq
from collections import defaultdict
input = sys.stdin.readline
V, E = map(int, input().split())
def dijkstra(graph, start):
distances = {node: float('inf') for node in range(1, V+1)}
distances[start] = 0
priority_queue = [(0, start)]
while priority_queue:
curr_dist, curr_node = heapq.heappop(priority_queue)
if curr_dist > distances[curr_node]:
continue
for neighbor, weight in graph[curr_node]:
distance = curr_dist + weight
if distance < distances[neighbor]:
distances[neighbor] = distance
heapq.heappush(priority_queue, (distance, neighbor))
return distances
# 초기화
graph = defaultdict(list)
for i in range(E):
u, v, w = map(int, input().split())
graph[u].append((v, w))
graph[v].append((u, w))
M, x = map(int, input().split())
M_list = list(map(int, input().split()))
S, y = map(int, input().split())
S_list = list(map(int, input().split()))
# 모든 집에 대한 다익스트라 실행
result = []
for node in range(1, V+1):
min_m = []; min_s = []
if node in M_list or node in S_list:
continue
dist = dijkstra(graph, node)
for m in M_list:
if dist[m] <= x:
min_m.append(dist[m])
for s in S_list:
if dist[s] <= y:
min_s.append(dist[s])
if min_m and min_s:
result.append(min(min_m)+min(min_s))
if result:
print(min(result))
else:
print(-1)이 방식은 모든 집을 다익스트라로 조사하고 각 집마다 맥세권과 스세권을 조사해서 맥세권과 스세권을 만족하는 집 중 최단거리의 합의 최솟값을 갱신하는 구조이다.
이 경우 다익스트라가 O(E log V) 라서 벌써 최대 1,500,000인데 V가 최대 10,000이므로
O(VE log V)는 최대 15,000,000,000 이나 된다.
고로 시간초과가 날 수 밖에 없다.
