그래프 (Python)

sliver gun·2025년 6월 13일
알고리즘파이썬

알고리즘

목록 보기
24/30

그래프 알고리즘 종류

  • DFS, BFS
  • 다익스트라
  • 벨만-포드
  • 플로이드-워셜

기타 등등이 있지만 일단 간략하게 이 4가지 알고리즘에 대한 문제들과 왜 이 알고리즘으로 풀어야 하는지에 대해 공부해보도록 하겠다.

이미 이 글에서 작성한 내용에서 문제 풀이를 추가하는 방식으로 작성하겠다.

DFS, BFS

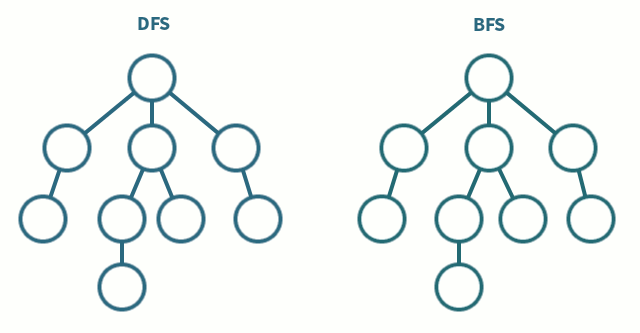
📌 DFS
한 방향을 기준으로 끝까지 탐색하고, 더 이상 갈 곳이 없을 때 뒤로 돌아와서 경로 탐색
재귀, 스택으로 구현
백트래킹 문제로 나옴

문제 (BOJ 1012 - 유기농 배추)

https://www.acmicpc.net/problem/1012

주어진 배추밭 (가로x세로)에 배추가 배치되고, 상하좌우가 인접의 기준이라고 할 때 몇 개의 덩어리가 있는지 알아내는 문제

💡 DFS는 보통 이런 2차원 배열에 있는 인덱스를 탐색하는 방식의 문제로 이루어져 있다.
보통 백트래킹 기반은 재귀 함수를 이용해 풀게 된다.

def worm(x, y, prev):
    if L[y][x] == 1:
        L[y][x] = 0
        if x+1 != M and prev != 2:
            worm(x+1, y, 0)
        if y+1 != N and prev != 3:
            worm(x, y+1, 1)
        if x-1 != -1 and prev != 0:
            worm(x-1, y, 2)
        if y-1 != -1 and prev != 1:
            worm(x, y-1, 3)
        if prev == -1:
            return 1
    return 0

def find(M, N):
    cnt = 0
    for i in range(N):
        for j in range(M):
            cnt += worm(j, i, -1)
    return cnt

for i in range(int(input())):
    M, N, K = map(int, input().split())
    L = [[0]*M for _ in range(N)]
    for j in range(K):
        x, y = map(int, input().split())
        L[y][x] = 1
    print(find(M, N))

위와 같이 인접 기준(상하좌우)를 차례대로 탐색하면서 재귀함수를 통해 인접한 모든 칸을 탐색하도록 코드를 짜는 것이 기본이다.

이 문제의 경우 인접한 칸을 발견할 때마다 넓이를 계산해야 하므로 cnt를 세는 과정을 따로 적어두어야 한다.

📌 BFS
현재 노드 기준 인접한 노드들을 먼저 탐색하는 방식
큐를 통해 구현
최단 거리를 찾을 때

  • 노드 순회 문제, 최단 경로 문제, 연결 요소 문제, 땅따먹기 문제

문제 (BOJ 2178 - 미로 탐색)

https://www.acmicpc.net/problem/2178

NxM 크기의 미로가 있을 때 (1,1) 에서 (N, M)으로 가는 최소 이동 칸 수를 구하는 문제

💡
BFS 또한 2차원 배열이나 그래프로 되어있는 문제에서 적용할 수 있으며, Queue를 사용해 문제를 풀 수 있다.
이 문제는 최단 경로를 구하므로 BFS를 이용해 풀 수 있다.

import queue

N, M = map(int, input().split())

Map = [[int(d) for d in str(input())] for _ in range(N)]
cnt = [[0 for _ in range(M)] for _ in range(N)]

Q = queue.Queue()

def bfs(x, y):
    Q.put((x, y))
    Map[x][y] = 0
    cnt[x][y] = 1

    while not Q.empty():
        x, y = Q.get()

        for dx, dy in ((-1, 0), (1, 0), (0, -1), (0, 1)):
            nx, ny = x + dx, y + dy

            if 0 <= nx < N and 0 <= ny < M and Map[nx][ny] == 1:
                if Map[nx][ny] == 1:
                    cnt[nx][ny] = cnt[x][y] + 1
                    Map[nx][ny] = 0
                    Q.put((nx, ny))

bfs(0, 0)
print(cnt[N - 1][M - 1])

BFS는 처음 조사하는 칸을 큐에 넣고, while문으로 큐가 빌 때까지 조사하는 방식으로 문제를 풀면 된다.

이미 방문한 노드 체크, 큐에 삽입 제거, 카운트 세기 와 같은 필요한 조작들을 빼먹지 않는다면 쉽게 풀 수 있다.

다익스트라

💡 가중치가 있는 그래프에서 특정 노드에서 다른 모든 노드까지의 최단 경로를 구하는 알고리즘
단, 음의 가중치가 없어야 함

문제 (BOJ 1446 - 지름길)

0부터 D까지 단방향 고속도로가 있다.
지름길의 출발구간과 도착구간과 지름길 길이를 주고 0에서 D까지 가는 최단거리를 구하시오.

💡 이 문제도 각 노드(구간) 사이에 가중치(길이)가 있으며, 최단거리를 구하는 문제이다.

N, D = map(int, input().split())
node = [0, D]; L = []
for _ in range(N):
    start, end, dist = map(int, input().split())
    L.append([start, end, dist])
    if end <= D:
        node.append(start)
        node.append(end)

node = sorted(list(set(node)))

# [dictonary에 하나씩 넣기]
dict = {}
for n in node:
    dict[n] = {}
dict[0][D] = D
for i in L:
    # 시작 위치, 끝 위치, 거리 입력
    start, end, dist = i

    if end > D:
        continue
    
    # 지름길 표시
    if end not in dict[start] or dist < dict[start][end]:
        dict[start][end] = min(dist, end - start)
    
    # 지름길 앞길 표시
    if start > 0:
        prev = node[node.index(start) - 1]
        if start not in dict[prev] or start - prev < dict[prev][start]:
            dict[prev][start] = start - prev

    # 지름길 뒷길 표시
    if end < D:
        next = node[node.index(end) + 1]
        if next not in dict[end] or next - end < dict[end][next]:
            dict[end][next] = next - end

# 우선순위 큐로 다익스트라 실행
import heapq

def dijkstra(dict, start):
    distance = {node: float('inf') for node in dict}
    distance[start] = 0
    queue = [(0, start)]

    while queue:
        cur_dist, cur_node = heapq.heappop(queue)

        if cur_dist > distance[cur_node]:
            continue

        for neighbor, weight in dict[cur_node].items():
            distance_to_neighbor = cur_dist + weight

            if distance_to_neighbor < distance[neighbor]:
                distance[neighbor] = distance_to_neighbor
                heapq.heappush(queue, (distance_to_neighbor, neighbor))
    return distance

res = dijkstra(dict, 0)
print(res[D])

⛔ 이 코드는 백준에 돌려도 통과되진 않습니다.
0부터 D까지의 1칸 간격 노드들을 모두 연결시켜 놓고 풀어야 한다고 합니다.
그럼 왜 testcase.ac에서 반례를 찾을 수 없는걸까요

다익스트라는 우선순위 큐를 이용해서 푼다.

우선순위 큐 안에서 시작점을 넣어놓고 인접 노드들을 방문하면서 인접 노드들의 최소 거리를 갱신하면서 큐에 추가하고 더 이상 탐색할 노드들이 없어 우선순위 큐가 빌 때까지 조사하는 방식이다.

이 알고리즘의 작동방식과 우선순위 큐의 원리를 알아야 적용할 수 있으며, 문제에 따라 노드를 어떻게 생성하고 준비하는지에 난이도가 달라질 것 같다.

플로이드 워셜

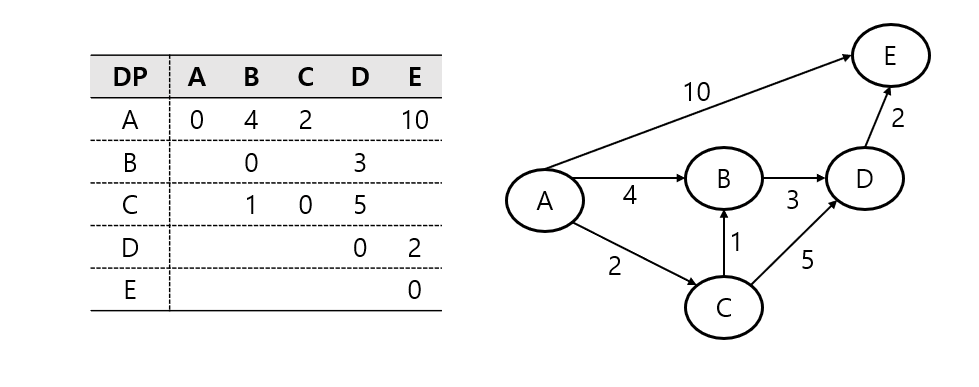
💡 모든 노드 간 최단 경로를 구하는 알고리즘
음의 가중치를 가진 간선이 있어도 작동한다.
DP(동적 계획법)을 기반으로 함

문제 (BOJ 1058 - 친구)

사람 수 N이 주어지고 2차원 배열로 각 사람이 친구인지 알려주는 표가 주어진다.
A와 B가 ‘2-친구’ 이려면 A와 B가 친구사이거나 A와 B가 한 다리 건너 친구여야한다.
2-친구가 가장 많은 사람의 2-친구를 구하시오

💡 플로이드 워셜은 인접 노드 거리와 특정 노드를 거쳐 가는 거리 중 짧은 거리를 갱신하는 알고리즘이다.
플로이드 워셜은 삼중 for문으로 해결하므로 O(N^3)을 견딜 수 있는 입력 값이 작은 문제여야 한다.
이 문제도 N이 최대 50이므로 플로이드 워셜에 적합하다.

N = int(input())
M = []
for i in range(N):
    M.append(list(''.join(input().split(" "))))

adj = [[0] * N for _ in range(N)]

for k in range(N):
    for i in range(N):
        for j in range(N):
            if i == j:
                continue
            if M[i][j] == 'Y' or (M[i][k] == 'Y' and M[k][j] == 'Y'):
                adj[i][j] = 1

res = []
for i in adj:
    res.append(sum(i))
print(max(res))

벨만 - 포드

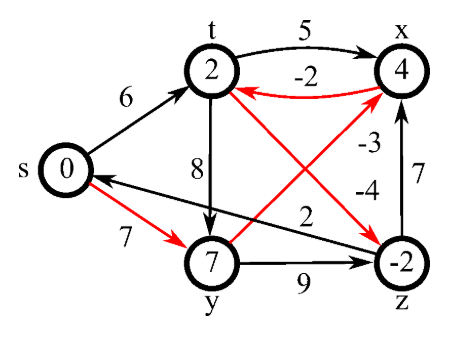
💡 가중치가 있는 그래프에서 특정 노드에서 다른 모든 노드까지의 최단 경로를 구하는 알고리즘
음의 가중치가 있는 그래프에서도 작동한다.
음의 가중치 사이클도 탐지 가능하다.

문제 BOJ 11657 - 타임머신

N개의 도시와 각 도시를 잇는 M개의 노선이 있다.
각 노선은 C의 시간이 걸리는데 이는 양수 뿐만 아니라 0일 수도, 음수일 수도 있다.
1번 도시에서 나머지 도시로 가는 가장 빠른 시간을 각각 구하시오.

💡 이 문제는 하나의 정점에서 나머지 정점으로 가는 모든 최단 경로를 구하며, 음의 가중치를 포함하고 있기 때문에 벨만 포드 알고리즘으로 풀기에 적합하다.

N, M = map(int, input().split())
graph = []
for i in range(M):
    A, B, C = map(int, input().split())
    graph.append((A, B, C))

dist = [float('inf') for _ in range(N+1)]
dist[1] = 0
for i in range(1, N+1):
    for start, end, cost in graph:
        if dist[start] != float('inf') and dist[end] > dist[start] + cost:
            dist[end] = dist[start] + cost
            if i == N:
                print(-1)
                exit()
for cost in dist[2:]:
    if cost == float('inf'):
        print(-1)
    else:
        print(cost)

요약

알고리즘탐색 방식구현 방식사용 목적/상황특징 및 조건
DFS한 방향 끝까지 탐색 후 백트래킹재귀, 스택백트래킹 문제, 그래프 탐색더 이상 갈 곳 없을 때 되돌아가는 방식
BFS현재 노드의 인접 노드부터 탐색큐최단 거리, 노드 순회, 연결 요소, 땅따먹기 문제최단 거리 보장 (같은 가중치일 때), 레벨 순 탐색 가능
다익스트라최단 거리 탐색우선순위 큐 (힙 등)하나의 노드 → 모든 노드 최단 경로음의 가중치 X, 양의 가중치에서만 정확함
플로이드 워셜모든 경로 탐색2차원 DP 테이블모든 노드 → 모든 노드 최단 경로음의 가중치 허용, 시간복잡도 O(V³)
벨만-포드간선 반복 갱신반복 루프하나의 노드 → 모든 노드 최단 경로음의 가중치 O, 음의 사이클 탐지 가능, O(VE) 시간복잡도
profile
sliver gun
이전 포스트

[Python] 그래프

다음 포스트

프로그래머스 고득점 Kit - 해시

0개의 댓글