Intro👀
먼저 방정식의 근이란 을 만족하는 x값의 집합을 의미한다.
방정식의 근의 종류
- 외재적 근 : 에서 x를 한쪽 변으로 분리 가능 → ( 참해 ) 꼴로 나옴
- 내재적 근 : 에서 x를 한쪽 변으로 분리 불가능 → 대입법, 시행착오법
수치해석은 외재적근이든, 내재적근이든 근의 종류와 상관없이 시행착오법(Trial and Error method)으로 구함, 근사해이기 때문에 오차가 존재함
근을 구하는 방법
- 구간법 : 가 존재할때 어떤 구간 를 설정하여 인 근을 찾아감 ( Bisection )
- 개방법 : 어떤 한 점( Initial Value )으로부터 시작해서 찾아감 ( Newton-Raphson )
Body🚩
이번 시간에는 Non-linear Eq( 비선형 방정식 )에서 해를 구하는 방법 중 첫번째, 이분법( Bisection method )에 대해 알아보자.
이분법을 설명하기에 앞서 ㄱ
근의 존재 여부
- 중간값 정리 : 어떤 함수 가 에서 연속이고 미분가능할때, 임의의 함수값 이 두 점에서의 함수값 와 다음과 같은 관계가 성립한다면,
이때 함수값 을 만족하는 값 c가 구간 에 존재하며 이다.즉, 이면 방정식의 근을 의미하고, 가 성립한다.
연속함수 이기때문에 , 이고, 는 함수의 근이 된다.
함숫값 의 부호가 같을때, 해의 갯수가 등 짝수개의 해를 가짐( But 해가 개인 경우 발생 )
반면에 함숫값 의 부호가 다르면 등의 홀수개의 해가 생김( 최소한 해가 개이상 존재함, 즉 해가 반드시 존재 )
※ 물론 중근을 가지거나 설정한 구간과 근이 겹칠경우( 해에 대응하는 함숫값이 인 경우 ) 두 함숫값의 부호가 홀수가 아닌 이 나올수도 있다.
결론적으로는 구간 설정시, 반드시 근의 존재여부를 확인해야한다. 우리는 중간값정리를 통해서 근의 존재여부를 확인하도록 하겠다.
이제 이분법에 대해 알아보자.
- 이분법
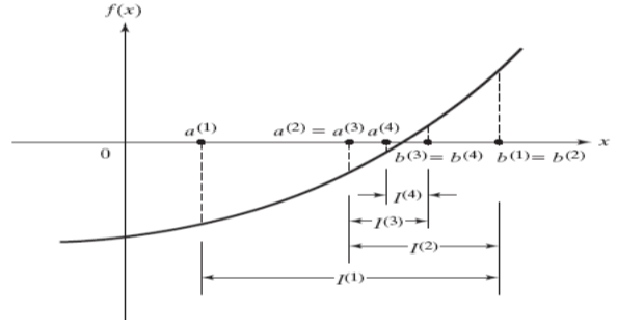
- 구간의 양 끝값인 의 중간값 를 정의한다.
- 두 함숫값 의 부호를 비교한다. ( 단지 a와c의 값을 비교하면 안됨!!! )
- -1. 두 함숫값의 부호가 다르다면, 새로운 구간인 으로 구간을 대체한다.
-2. 두 함숫값의 부호가 같다면, 새로운 구간 으로 구간을 대체한다.
이렇게 표현할 수 있는 이유는 그래프를 그려보면 간단히 직관적으로 파악할 수 있다.
Code💻
2 구간법 , 이분법 코딩 순서
1. 함수정의
f(x) => 여기서 말하는 함수는 1번 함수말함
(2가지 파이썬 함수) (1) sum , print (2) def
2. 구간설정
[a,b] 구간 설정
3. 새로운 구간을 설정하기 위한 새로운 변수 정의
c= (a+b)/2
4. 새로운 변수가 들어간 함수값의 부호 판단
5. 새로운 변수로 구간 재설정
