📝 주식가격 (Level 2)
스택/큐
주식가격
🔹Python
- 나의 풀이
def solution(prices):
answer = []
length = len(prices)
queue = [(i,p) for i,p in enumerate(prices)] # 각 price의 인덱스와 값을 튜플로 묶어 큐에 저장
while len(queue) > 0: # 큐가 빌 때까지
cur = queue.pop(0) # 큐의 첫 번째 요소를 꺼냄
if all(cur[1] <= q[1] for q in queue):
answer.append(length - cur[0] - 1)
else: # !all(cur[1] <= q[1] for q in queue):
for i in range(len(queue)):
if cur[1] > queue[i][1]:
answer.append(queue[i][0] - cur[0])
return answer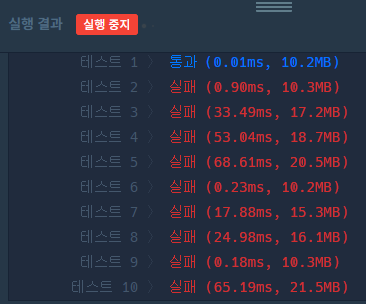
테스트 케이스만 맞고 다 틀렸음ㅋㅋ
그래도 어떻게 풀었는지 설명을 써보겠다.
queue = [(i,p) for i,p in enumerate(prices)]를 사용해 각 price의 인덱스와 값을 튜플로 묶어 큐에 저장했다. 이렇게 하면 index값을 이용해 주식 가격의 위치를 파악할 수 있어서 사용했다.
if all(cur[1] <= q[1] for q in queue):를 사용해 모든 queue의 값보다 현재 값이 작거나 같으면 가격이 떨어지는 일이 없다는 뜻이므로
answer.append(length - cur[0] - 1) queue 전체 길이에서 현재 price의 인덱스 값을 빼주어서 answer에 append 했다.
else: # !all(cur[1] <= q[1] for q in queue): else 즉, 현재 값이 모든 queue의 값보다 작지 않을 때 즉, queue에 있는 값들 중에 가장 클 때
if cur[1] > queue[i][1]: 만약 현재 값이 다른 queue 값보다 크나면
answer.append(queue[i][0] - cur[0]) 두 값의 인덱스 차이만큼 계산해서 answer에 append한다.
근데 다시 생각해봐도 모르겠어서 gpt 돌려봤다 ..
- gpt 풀이
def solution(prices):
answer = [0] * len(prices)
stack = []
for i, price in enumerate(prices):
# 스택이 비어있지 않고 현재 가격이 스택의 맨 위 가격보다 낮을 때
while stack and price < prices[stack[-1]]:
j = stack.pop()
answer[j] = i - j
stack.append(i)
# 스택에 남아있는 인덱스는 가격이 끝까지 떨어지지 않은 경우
while stack:
j = stack.pop()
answer[j] = len(prices) - j - 1
return answer-
초기화: 각 가격에 대해 가격이 떨어지기까지 걸리는 일수를 저장할 결과 리스트 answer를 0으로 초기화합니다. 이 리스트는 주어진 prices 리스트와 같은 길이를 가집니다.
-
스택 사용: 스택을 사용하여 가격의 인덱스를 저장합니다. 스택을 사용하면 더 효율적으로 가격이 떨어지는 시점을 찾을 수 있습니다.
-
가격 비교: 주어진 가격 리스트를 순회하면서 현재 가격이 스택의 맨 위에 있는 가격보다 낮으면, 해당 인덱스를 스택에서 꺼내고 결과 리스트에 가격이 떨어지는 시점을 계산하여 저장합니다.
answer리스트는 각 가격이 떨어지기까지 걸리는 일수를 저장합니다.stack은 가격의 인덱스를 저장합니다.for 루프는 주어진 가격 리스트를 순회하면서 현재 가격이 스택의 맨 위에 있는 가격보다 낮으면 해당 인덱스를 스택에서 꺼내고, 그 인덱스의 결과 값을 현재 인덱스와 꺼낸 인덱스의 차이로 저장합니다.- 루프가 끝난 후에도 스택에 남아있는 인덱스는 끝까지 가격이 떨어지지 않은 경우이므로, 이 경우 남아있는 일수를 계산하여 저장합니다.
이 방법은 시간 복잡도가 O(n)으로, 각 가격을 한 번씩만 처리하므로 매우 효율적입니다.
📚 배울 점
Stack(LIFO) 기본연산
push()스택에 원소를 추가한다.pop()스택 가장 위에 있는 원소를 삭제하고 그 원소를 반환한다.peek()스택 가장 위에 있는 원소를 반환한다. (삭제하지는 않는다.)empty()스택이 비어있다면 1, 아니면 0을 반환한다.
🔸Java
- 다른 사람의 풀이
import java.util.*;
class Solution {
public int[] solution(int[] prices) {
Stack<Integer> beginIdxs = new Stack<>();
int i=0;
int[] terms = new int[prices.length];
beginIdxs.push(i);
for (i=1; i<prices.length; i++) {
while (!beginIdxs.empty() && prices[i] < prices[beginIdxs.peek()]) {
int beginIdx = beginIdxs.pop();
terms[beginIdx] = i - beginIdx;
}
beginIdxs.push(i);
}
while (!beginIdxs.empty()) {
int beginIdx = beginIdxs.pop();
terms[beginIdx] = i - beginIdx - 1;
}
return terms;
}
}Stack보다 Deque를 사용하는 것이 좋다고 공식문서에 적혀있다. 따라서 Deque를 사용한 코드로 바꿔보았다.
import java.util.Deque;
import java.util.ArrayDeque;
class Solution {
public int[] solution(int[] prices) {
Deque<Integer> beginIdxs = new ArrayDeque<>();
int[] terms = new int[prices.length];
beginIdxs.push(0); // Push the initial index onto the deque
for (int i = 1; i < prices.length; i++) {
while (!beginIdxs.isEmpty() && prices[i] < prices[beginIdxs.peek()]) {
int beginIdx = beginIdxs.pop();
terms[beginIdx] = i - beginIdx;
}
beginIdxs.push(i);
}
// After processing all elements, handle remaining indices in the deque
int lastIndex = prices.length;
while (!beginIdxs.isEmpty()) {
int beginIdx = beginIdxs.pop();
terms[beginIdx] = lastIndex - beginIdx - 1;
}
return terms;
}
}
Stack<Integer> beginIdxs = new Stack<>();
-> Deque<Integer> beginIdxs = new ArrayDeque<>();
