정의
조합
조합론에서 조합(combination)은
집합에서 서로 다른 n개의 원소 중에서
순서에 상관없이 r개를 선택하는 것이다.
그 경우의 수는 이항계수이다.
방법
STL 사용
next_permutation(v.begin() , v.end())전체 n개의 원소들 중에서 r개를 뽑는 조합(=nCr)을 구한다면
n개의 벡터 원소에 1을 r개 0을
나머지인 n-r개 집어넣어서 순열을 돌리고
1에 해당하는 인덱스만 가져오면 된다.
DFS로 구현
조합
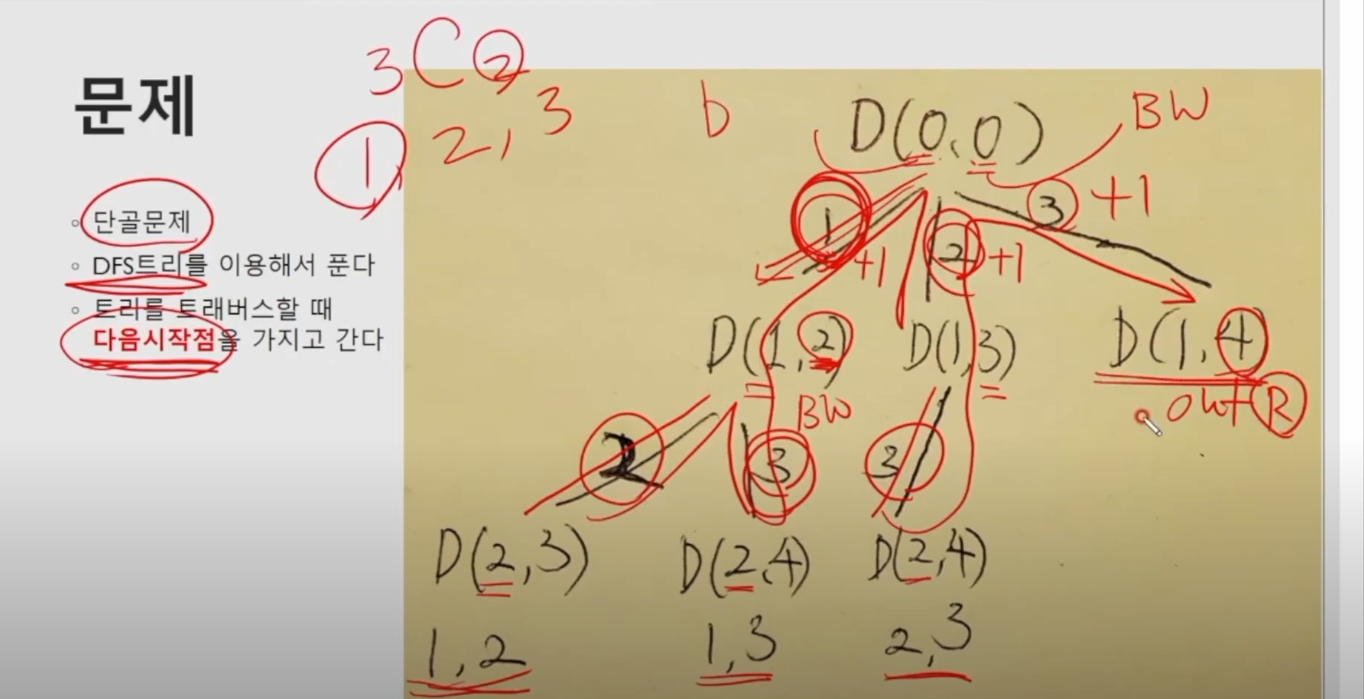
조합을 구현할 때, 하나의 시작점을 정한다면,
그 시작점 이전에 나온 원소들을 다시 쳐다보지 말자 !
코드
STL 사용
#include <stdio.h>
#include <vector>
#include <algorithm>
using namespace std;
int main (){
// 1부터 6까지 담을 벡터
vector<int> n;
// 1부터 6까지 생성
for(int i=0; i<6; i++){
n.push_back(i+1);
}
// 0과1을 저장 할 벡터 생성
vector<int> ind;
// k=4, 4개를 뽑으니까
int k = 4;
// k개의 1 추가
for(int i=0; i<k; i++){
ind.push_back(1);
}
// 2개(6개-2개)의 0 추가
for(int i=0; i<n.size()-k; i++){
ind.push_back(0);
}
// 정렬
sort(ind.begin(), ind.end());
//순열
do{
// 출력
for(int i=0; i<ind.size(); i++){
if(ind[i] == 1){
printf("%d ", n[i]);
}
}
printf("\n");
}while(next_permutation(ind.begin(), ind.end()));
return 0;
}DFS로 구현
#include <iostream>
using namespace std;
// nCr
int r = 2;
int n[] = {1, 2, 3};
int result[] = {0, 0};
void DFS(int L, int BeginWith){
// 종료 조건
if (L == r){
for(int i=0; i<r; i++){
cout << result[i] << ", ";
}
cout << endl;
}
else{
for(int i=BeginWith; i<(sizeof(n)/sizeof(int)); i++){
result[L] = n[i];
DFS(L+1, i+1);
}
}
}
int main(){
DFS(0, 0); // 0 level, 0 BeginWith
}