정의
Sorting(정렬)
n개의 숫자가 입력으로 주어졌을 때, 이를 기준에 맞게 정렬하여 출력하는 알고리즘
정렬 알고리즘에는 다양한 종류가 있고, 이에 따라 수행 시간도 다양하다.
종류
Selection Sort(선택 정렬)
정의
순차적으로 기준에 따라 현재 위치에 들어갈 값을 찾아 정렬
오름차순이면 Min-Selection Sort(최소 선택 정렬)
내림차순이면 Max-Selection Sort(최대 선택 정렬)
방법
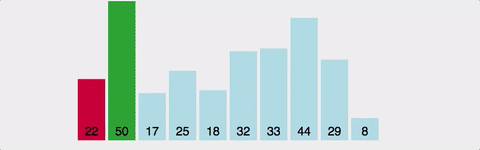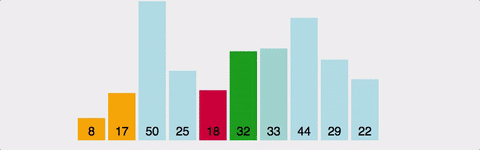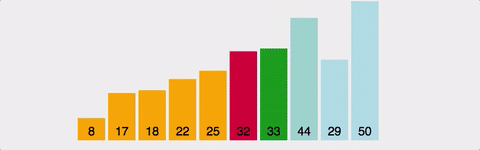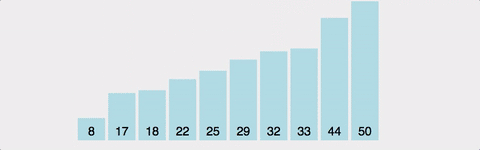
- 정렬되지 않은 배열의 맨 앞부터, 이를 포함한 그 이후의 배열값 중 가장 작은 값(혹은 가장 큰 값)을 찾아간다.
- 교환한다.
- 1~2를 반복한다.
장단점
👍 장점
- 구현이 간단하다.
- 데이터를 하나씩 비교하기 때문에 정밀한 비교가 가능하다.
- 비교하는 횟수에 비해 교환하는 횟수가 적다.
👎 단점
- 데이터를 하나씩 비교하기 때문에 시간이 오래 걸린다.
- 정렬된 상태에서 새로운 데이터가 추가되면 정렬 효율이 좋지 않다.
복잡도
- 시간 복잡도 :
O(n^2)(n-1, n-2, ..., 1개씩 비교 반복. 전체 비교를 진행하므로) - 공간 복잡도 :
O(n)(하나의 배열에서만 진행하므로)
코드
#include
using namespace std;
void selectionSort(int arr[], int size) {
for(int i = 0 ; i < size - 1 ; i++) {
for (int j = i + 1 ; j < size ; j++) {
if(arr[i] > arr[j]) {
swap(arr[i], arr[j]);
}
}
}
}
int main() {
int arr[] = {9,8,7,4,2,6,1,3, 5};
int size = sizeof(arr) / sizeof(arr[0]);
selectionSort(arr, size);
for(int i = 0 ; i < size ; i++) {
cout << arr[i] << " ";
}
cout << endl;
return 0;
}
출처: https://unikys.tistory.com/357 [All-round programmer]Bubble Sort(버블 정렬)
정의
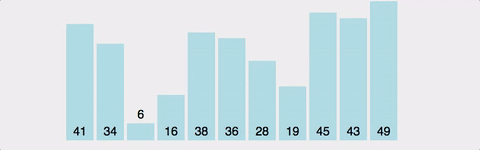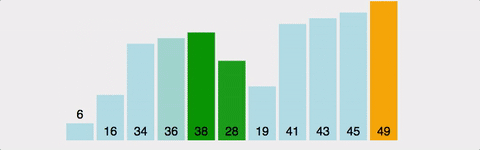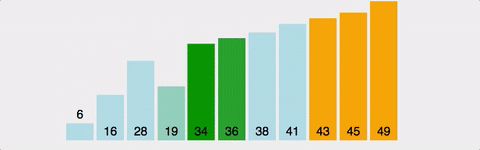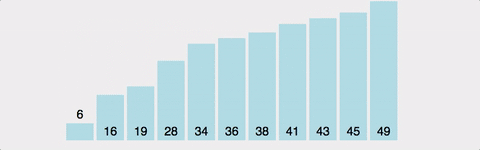
연속된 두 개의 인덱스를 비교하여, 정한 기준의 값을 뒤로 넘겨 정렬한다.
오름차순이면 큰 값이 뒤로 이동
방법
- 왼쪽 값과 오른쪽 값을 비교하여 큰 값(혹은 작은 값)을 뒤로 보낸다.
전체 배열의 크기 - 현재까지 순환한 바퀴 수만큼 반복한다
장단점
👍 장점
- 구현이 간단하다.
- 데이터를 하나씩 비교하기 때문에 정밀한 비교가 가능하다.
👎 단점
- 데이터를 하나씩 비교하기 때문에 비교 횟수가 많아지므로 시간이 오래 걸린다.
복잡도
- 시간 복잡도
O(n^2)(n-1, n-2, ..., 1개씩 비교 반복. 전체 비교를 진행하므로) - 공간 복잡도 :
O(n)(하나의 배열에서만 진행하므로)
코드
#include
using namespace std;
void bubbleSort(int arr[], int size) {
bool isSwap;
do {
isSwap = false;
for (int i = 1 ; i < size ; i++) {
if (arr[i - 1] > arr[i]) {
swap(arr[i - 1] , arr[i]);
isSwap = true;
}
}
} while(isSwap);
}
int main() {
int arr[] = {9,8,7,4,2,6,1,3, 5};
int size = sizeof(arr) / sizeof(arr[0]);
bubbleSort(arr, size);
for(int i = 0 ; i < size ; i++) {
cout << arr[i] << " ";
}
cout << endl;
return 0;
}
출처: https://unikys.tistory.com/357 [All-round programmer]Insertion Sort(삽입 정렬)
정의
버블정렬의 비효율 성을 개선하기 위해 등장
현재 위치에서 그 이하의 배열들을 비교해 자신이 들어갈 위치를 찾아 그 위치에 삽입하여 정렬
방법
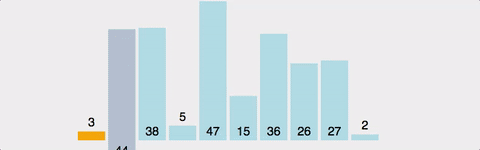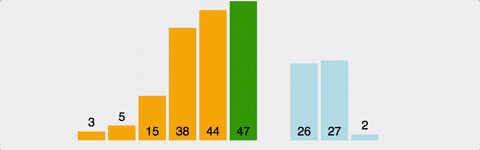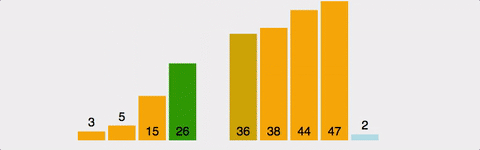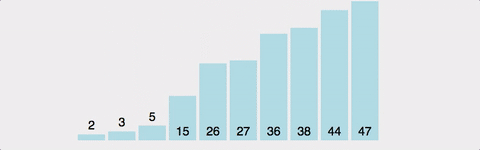
- 2번째 인덱스부터 시작한다.
- 왼쪽에 자기 자신보다 작은 수가 나올 때 까지 오른쪽으로 민다.
- 왼쪽에 자기 자신보다 작은 수가 나오면 삽입한다.
- 2~3을 반복한다.
장단점
👍 장점
- 입력으로 들어오는 배열의 원소가 정렬되어있을수록 속도가 빠르다.
- 정렬된 값은 교환이 일어나지 않는다.
👎 단점
- 삽입을 구현해야 하므로 속도가 자료구조의 영향을 많이 받는다.
- 입력으로 들어오는 배열이 역순으로 정렬된 경우 성능이 굉장히 좋지 않다.
복잡도
- 시간 복잡도 :
역으로 정렬되어 있을 경우 =O(n^2)(n-1, n-2, ..., 1개씩 비교 반복. 전체 비교를 진행하므로)
이미 정렬되어 있는 경우 =O(n)(1번씩만 비교함) - 공간 복잡도 :
O(n)(하나의 배열에서만 진행하므로)
코드
#include
using namespace std;
void insertionSort(int arr[], int size) {
for(int i = 0 ; i < size - 1 ; i++) {
for (int j = i + 1 ; j >= 0 ; j--) {
if(arr[j - 1] > arr[j]) {
swap(arr[j - 1], arr[j]);
} else {
continue;
}
}
}
}
int main() {
int arr[] = {9,8,7,4,2,6,1,3, 5};
int size = sizeof(arr) / sizeof(arr[0]);
insertionSort(arr, size);
for(int i = 0 ; i < size ; i++) {
cout << arr[i] << " ";
}
cout << endl;
return 0;
}
출처: https://unikys.tistory.com/357 [All-round programmer]Merge Sort(병합 정렬)
정의
Divede and conquer(분할 정복) 방식으로 설계된 알고리즘.
Divede and conquer(분할 정복)
큰 문제를 반으로 쪼개 해결해 나가는 방식.
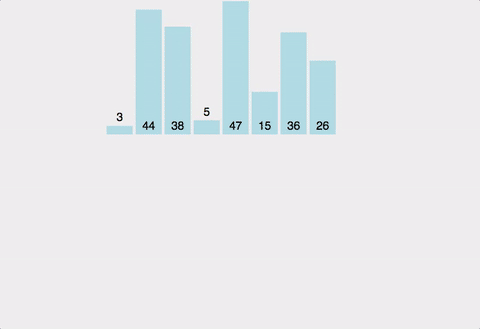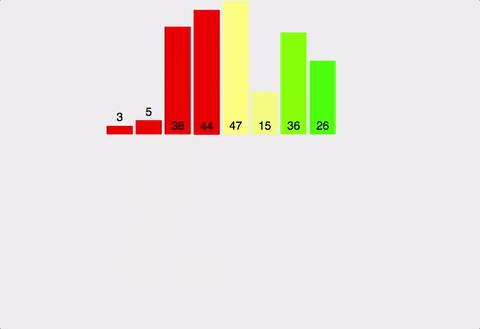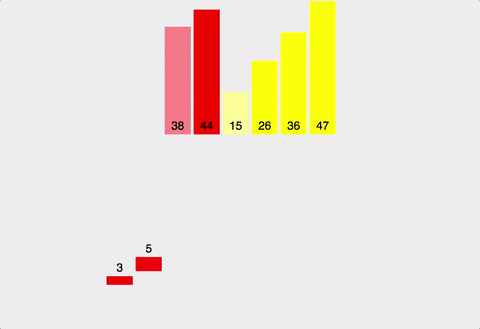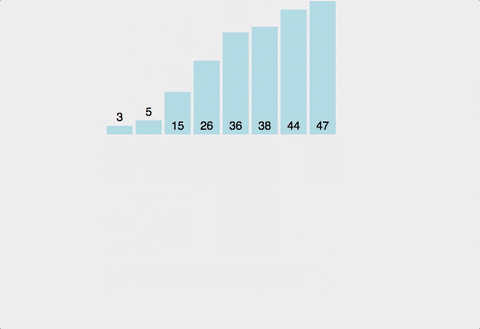
배열을 왼쪽 절반, 오른쪽 절반으로 분할해 최소 단위로 쪼갠 후 합병하며 정렬한다.
방법
- 분할
- 배열을 반으로 분할한다.
- 배열의 크기가 0이거나 1일때까지 1을 반복한다.
- 합병
- 두 배열의 앞에서부터 순차로 비교하여, 오름차순일 경우 작은 값을 새 임시 배열에 저장한다.
- 둘 중 한 배열이 다 저장되었다면 나머지 배열은 임시 배열에 저장한다.
- 1-2를 반복한다.
- 임시 배열을 원본 배열에 복사한다.
장단점
👍 장점
- 항상 일정한 시간 복잡도(O(NlogN))를 가진다.
- 안정적이며 대부분의 경우에서 좋은 성능을 낸다.
👎 단점
- 작은 단위로 쪼갠 배열을 저장할 공간을 사용하기 때문에 추가 메모리 공간이 필요하다.
복잡도
-
합병
두 배열 A,B를 정렬하기 때문에 A배열 크기 = N1, B배열 크기 = N2 라 하면 O(N1+N2)
이때 N = N1+ N2 이므로O(N)이라고 할 수 있다. -
분할
크기가 N인 배열을 분할하면 (N/2, N/2) -> (N/4, N/4, N/4, N/4) -> ... 이렇게 매번 반씩 감소한다.
lgN만큼 반복해야 크기가 1인 배열로 분할 할 수 있으므로O(lgN)이라고 할 수 있다. -
시간 복잡도 :
O(NlgN)(각 분할별로 합병을 진행하므로) -
공간 복잡도 :
O(2N)(정렬을 위한 배열을 하나 더 생성하므로)
코드
#include <iostream>
using namespace std;
void mergeSort(int arr[], int size) {
if (size > 2) {
mergeSort(arr, size / 2);
mergeSort(arr + size / 2, size - size / 2);
int leftCursor = 0;
int rightCursor = size / 2;
int buff[50];
int buffCursor = 0;
while (leftCursor < size / 2 && rightCursor < size) {
if (arr[leftCursor] < arr[rightCursor]) {
buff[buffCursor++] = arr[leftCursor++];
} else {
buff[buffCursor++] = arr[rightCursor++];
}
}
for (int i = leftCursor ; i < size / 2 ; i++) {
buff[buffCursor++] = arr[i];
}
for (int j = rightCursor ; j < size ; j++) {
buff[buffCursor++] = arr[j];
}
memcpy(arr, buff, size * sizeof(int));
} else {
if (arr[0] > arr[1]) {
swap(arr[0], arr[1]);
}
}
}
int main() {
int arr[] = {9,8,7,4,2,6,1,3, 5};
int size = sizeof(arr) / sizeof(arr[0]);
mergeSort(arr, size);
for(int i = 0 ; i < size ; i++) {
cout << arr[i] << " ";
}
cout << endl;
return 0;
}
출처: https://unikys.tistory.com/357 [All-round programmer]
Quick Sort(퀵 정렬)
정의
Divede and conquer(분할 정복) 방식으로 설계된 알고리즘.
pivot point라는 기준값을 설정해, 이 값을 기준으로 작은 값은 왼쪽, 큰 값은 오른쪽으로 옮기는 방식
이를 반복하여 분할된 배열의 크기가 1이 되면 모두 정렬된다.
최악의 경우에는 합병 정렬보다 느리지만 일반적으로는 퀵 정렬이 합병 정렬보다 20% 이상 빠르다.
방법
pivot point값을 설정한다. (보통 맨 앞이나 맨 뒤, 중간 인덱스 값이나 랜덤값으로 설정)pivot point를 기준으로 작은 요소들은 왼쪽, 큰 요소들은 오른쪽으로 옮겨진다.pivot point을 제외한 왼쪽 리스트와 오른쪽 리스트를 다시 정렬한다.- 부분 리스트에서도 다시 1-2를 반복한다.
- 부분 리스트의 크기가 0이나 1이 될 때까지 반복한다.
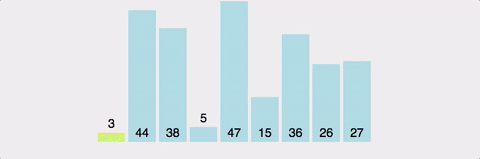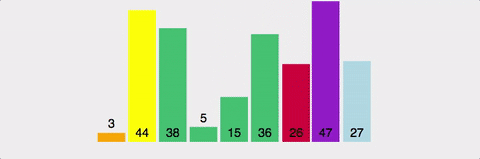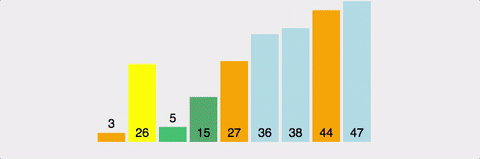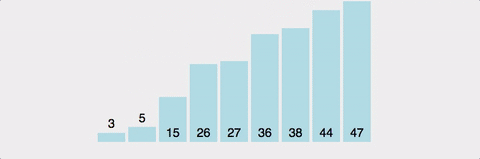
장단점
👍 장점
- 평균 실행 시간이 빠르다.
👎 단점
- 축(pivot)을 어떻게 설정하느냐에 따라 성능의 차이가 심하다.
- 안정성이 좋지 않다.
복잡도
- 시간 복잡도 :
O(NlgN)(분할과 동시에 정렬을 진행, 각 정렬은 배열의 크기 N만큼 비교하며, 이를 총 분할 깊이인 lgN만큼 진행하므로 총 비교횟수는 NlgN)
최악의 경우 (이미 배열이 정렬되어있는 경우) =O(N^2)(분할이 N만큼 일어나므로) - 공간 복잡도 :
O(log n)(재귀적 호출로 발생)
최악의 경우 =O(n)
코드
#include <iostream>
using namespace std;
void quickSort(int arr[], int size) {
int pivot = arr[0];
int cursor = 0;
for (int i = 1; i < size ; i++) {
if (pivot > arr[i]) {
cursor++;
swap(arr[cursor], arr[i]);
}
}
swap(arr[0], arr[cursor]);
if (cursor > 0) {
quickSort(arr, cursor);
}
if (cursor + 1 < size - 1) {
quickSort(arr + cursor + 1, size - cursor - 1);
}
}
int main() {
int arr[] = {9,8,7,4,2,6,1,3,5};
int size = sizeof(arr) / sizeof(arr[0]);
quickSort(arr, size);
for(int i = 0 ; i < size ; i++) {
cout << arr[i] << " ";
}
cout << endl;
return 0;
}
출처: https://unikys.tistory.com/357 [All-round programmer]정리
정렬 별 시간복잡도, 공간복잡도 비교
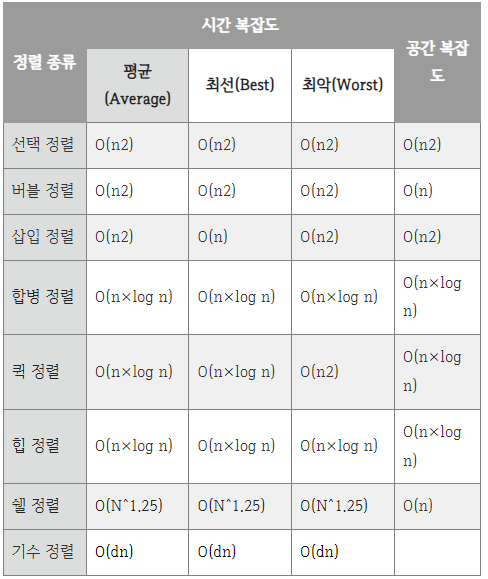
정렬 별 속도 비교

