Segment Tree (세그먼트 트리)
개념
주어진 쿼리에 대해 빠르게 응답하기 위해
만들어진 자료구조이다.
예시
1 2 3 4 5 6 이라는 배열 arr 이 있다.
arr[2] + arr[3] + arr[4]를 구하라는 쿼리가 주어진다.
쿼리란?
주어진 요구사항에 대해 맞는 결과물을 제시하라는 뜻
지금 당장은 3+4+5로 간단히 해결할 수 있다.
-
arr[3]을 10으로 바꾸고
-
다시 arr[2] + arr[3] + arr[4]를 구하라는 쿼리가 주어진다.
또 다시 arr[2] + arr[3] + arr[4]를 해야한다.
이렇게 되면 한번 실행하는데 걸리는 시간은
수를 바꾸는데 O(1),
수를 더하는데 O(N)이니
M번 수행한다 치면 O(MN + M) -> O(MN)의 시간이 걸린다.
필요성
방금 위에서 본 내용중
수를 바꾸는 과정과 수를 더하는 과정이
세그먼트 트리에서는
수를 바꾸는 과정 :: O(lgN)
수를 더하는 과정 :: O(lgN)
으로 변하게 된다.
M번 실행한다 치면 O(MlgN + MlgN) -> O(MlgN) 의 시간이 걸리게 된다.
시각적으로 확인해 볼 수있는 방법은 M = 100, N = 2^20이라 치자
O(MN)에서는 100*2^20 = 10,000,000(대략)
O(MlgN)에서는 100*20 = 2,000으로
데이터와 반복수행이 잦아질 수록 시간 복잡도 차이가 기하급수적으로 커진다.
(세그먼트 트리는 대부분 완전 이진 트리이다. 아래 그림을 통해 확인하자)
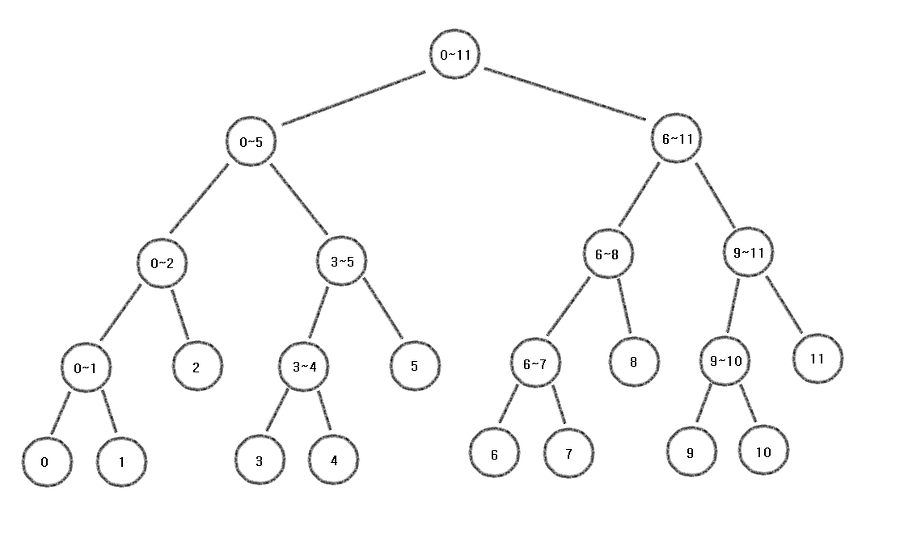
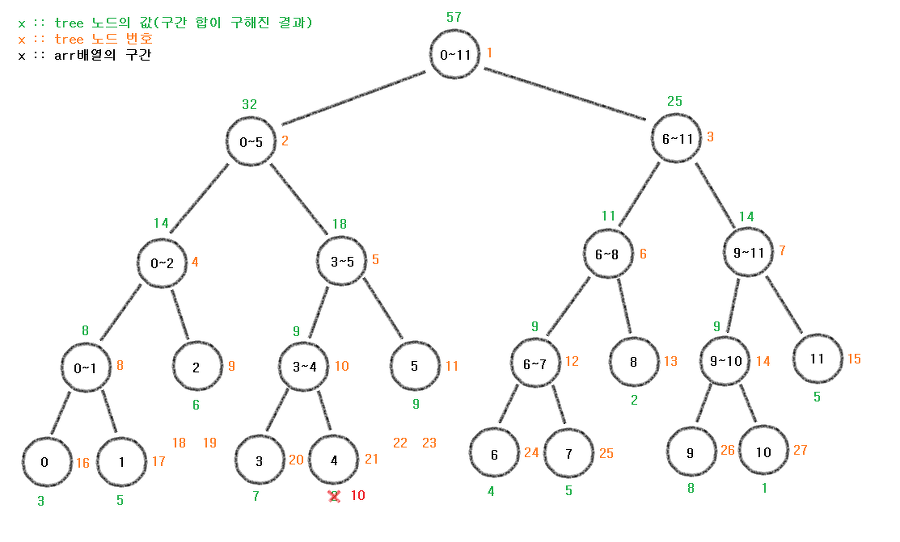
위의 그림은 N = 12일때 모습이다.
제일 아래 리프 노드로 달린 것들이
실제 우리가 처음 받아온 데이터들을 의미한다.
(여기서는 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11이라 적힌 노드들을 의미)
x~y 는
x부터 y까지의 합의 범위를 나타낸 것이다.
ex) arr[0] = 1, arr[1] = 2 면
0노드 = 1,
1노드 = 2
0~1노드 = 3이 들어간다.
결국 가장 최상위 루트 노드는 0~11이라 적혀있고,
처음 받아온 데이터들의 총 합을 의미한다.
세그먼트 트리의 전체 크기 구하기
아래 init함수를 만들기 전에,
우선 하나 알고 가야할 사실이 있다.
N = 12일 때의 세그먼트 트리의 전체 크기
(배열 사이즈 정하기)를 구하기 위해서는
2^k로 12보다 바로 큰 값을 만들 수 있는 k를 찾아야한다. 즉, k는 4이다.
그리고 난 뒤
2^k를 하면 16이 되고
16에 *2를 하면
우리가 원하는 세그먼트 트리의 크기를 구할 수 있다.
이 과정이 귀찮다면 그냥 N * 4를하면
(여기서는 48이 세그먼트 트리 크기가 될 것이다.)
메모리는 조금 더 먹지만, 편리하게 이용할 수 있다.
int h = (int)ceil(log2(n));
int tree_size = (1 << (h+1));
출처: https://www.crocus.co.kr/648 [Crocus]이렇게 나타낼 수 있는데
ceil은 올림을 하겠다는 의미이고,
log2N에서 도출되는 값을 올림한 값을 h에 저장한다.
즉 log2(12) = 3.xxx이고 올림한 4를 h에 저장한다.
1 << (4+1) = 1 << 5 = 32가 결국 tree_size가 된다.
크기가 N인 배열이 존재할 때
1. 트리의 높이 =ceil(log2(N))
2. 세그먼트 트리의 크기 = (1 << (트리의 높이 + 1) )
세그먼트 트리 만들기
Segment Tree node에 값들이 쌓이는 원리
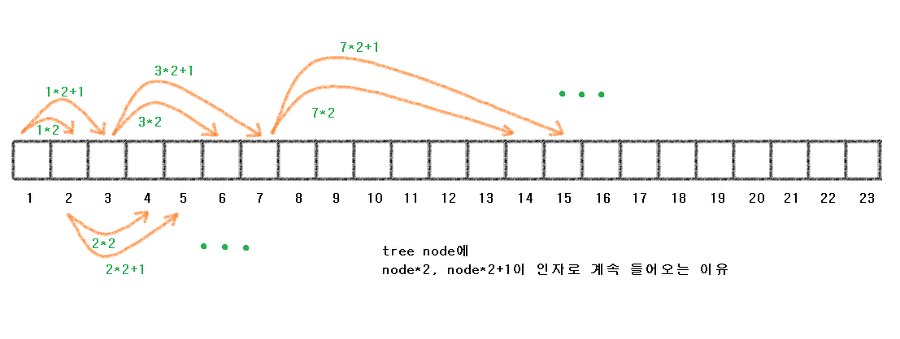
우리는 세그먼트 트리를 형성할 때
루트 노드 = 1로 생각한다.
이때 루트노드 왼쪽 노드 = 2번 노드가 될 것이고
오른쪽 노드 = 3번 노드가 될 것이다.
그리고 2번노드의 왼쪽 노드는 4번,
오른쪽 노드는 5번이 될 것이다.
또한 3번 노드의 왼쪽 노드는 6번,
오른쪽 노드는 7번이 될 것이다.
그림을 보면 알다시피
포인터로 동적할당을 통한 트리가 아닌
배열로 트리를 만들고 있다.
그 이유는 세그먼트 트리는 full binary tree에 가깝기에, 배열에 모든 값들이 꽉꽉차서 올 가능성이 매우 높기 때문에 포인터보다는 배열을 이용하게 된다.
그리고 각 노드마다의 왼쪽, 오른쪽 자식 노드는
항상 규칙이 정해져 있다.
<< 현재 노드의 번호가 node 일 때 >>
노드의 왼쪽 자식 배열 번호 ::node * 2
노드의 오른쪽 자식 배열 번호 ::node * 2 + 1
이 방식은 아래에 나오는 init 함수 및 다른 함수에서
node*2 , node*2+1 이 어떻게 이용되는지 알 수 있다.
주의할 점
이 내용을 보면서
tree 배열과 arr 배열을 햇갈리지 말아야 한다.
tree 배열은 세그먼트 트리가 만들어지는 배열이고
arr 배열은 처음에 입력받아 생성된 배열이다.
1. 초기화 과정(init)
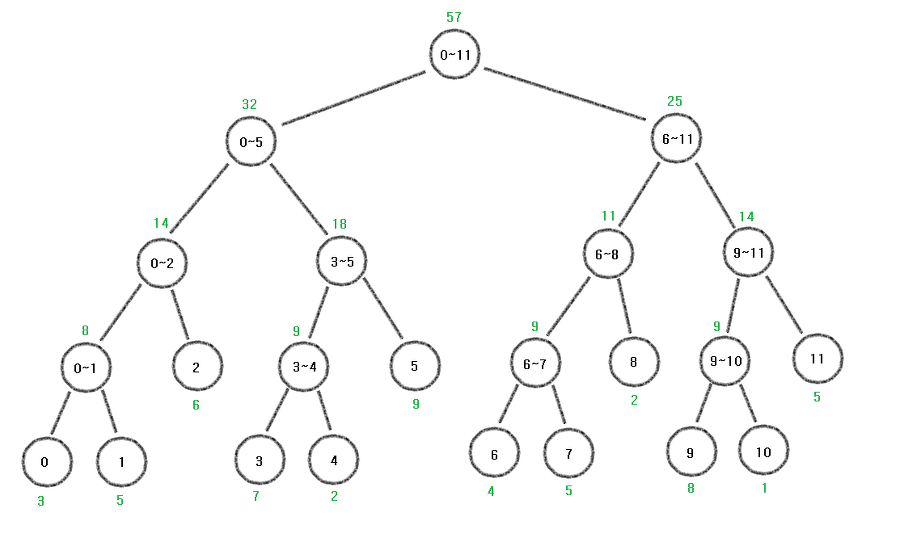
초기화라는 의미는 결국 위의 그림과 같은 트리를 생성하는 것이다.(가장 초기상태의 트리)
이 초기화 과정을 거치고 나면 결국 구간 합 트리가 형성된다.
만약 arr[12] = {3, 5, 6, 7, 2, 9, 4, 5, 2, 8, 1, 5}였다면 다음과 같은 구간 합 세그먼트 트리가 나올 것이다.
ll init(vector<ll> &arr, vector<ll> &tree, int node, int start, int end)
{
if (start == end)
return tree[node] = arr[start];
int mid = (start + end) / 2;
return tree[node] = init(arr, tree, node * 2, start, mid) + init(arr, tree, node * 2 + 1, mid + 1, end);
}
// This source code Copyright belongs to Crocus
// If you want to see more? click here >>
인자
ll init(vector<ll> &arr, vector<ll> &tree, int node, int start, int end)
arr벡터(배열)tree벡터(배열)- 노드번호, 노드의 시작번호, 노드의 끝번호
start == end 일 때
if (start == end)
return tree[node] = arr[start];tree[node] = arr[start]를 받는다.
start != end 일 때
return tree[node] = init(arr, tree, node * 2, start, mid) + init(arr, tree, node * 2 + 1, mid + 1, end); 위의 return tree[node] = init(~) + init(~) 로 들어가게 된다.
init인자로 자세히 보면 node*2 와 node*2+1이 있다.
위에서 언급했다시피
각 노드의 왼쪽 자식과 오른쪽 자식으로 분리되는 과정을 보여주는 것이다.
그리고 왼쪽 자식쪽에는 start ~ mid 를 보내고,
오른쪽 자식에는 mid+1 ~ end 를 보낸다.
(mid :: (start + end) / 2)
이 의미는 arr의 값을 반틈씩 쪼개어 계속 보내고 있는 것을 의미한다.
arr[12] = {3, 5, 6, 7, 2, 9, 4, 5, 2, 8, 1, 5}라고 했을 때
첫
init(arr, tree, node * 2, start, mid)에 의해 들어가는 인자를 숫자로 표현해보면
init(arr, tree, 2, 0, 5)이 들어간다.즉, 1번 루트 노드의 왼쪽 자식(2번 노드)에는 arr[0~5] ( = arr[start~mid) )값이 들어간다.
그다음
init(arr, tree, node * 2 + 1, mid+1, end)는
init(arr, tree, 3, 6, 11)다음과 같이 들어간다.즉, 1번 루트 노드의 오른쪽 자식(3번 노드)에는 arr[6~11]] ( = arr[mid+1~end) )값이 들어간다는 것이다.
다시 start == end 일 때
이제 다시 start == end의 의미를 파악해보자.
if (start == end)
return tree[node] = arr[start];노드가 계속 분할되어
결국 start와 end가 같아지는 부분이 생길 것이다.
이때 arr[start~end]가 arr[start]와 같다는 의미이고,
결국 노드의 범위가 1인 리프 노드를 의미한다.
따라서 가장 아래까지 내려왔다면 현재 node번째인 tree[node]에 arr[start]값을 대입해준다는 의미이다.
그림으로 확인해 본다면 다음과 같은 과정이 이루어 지는 것이다.
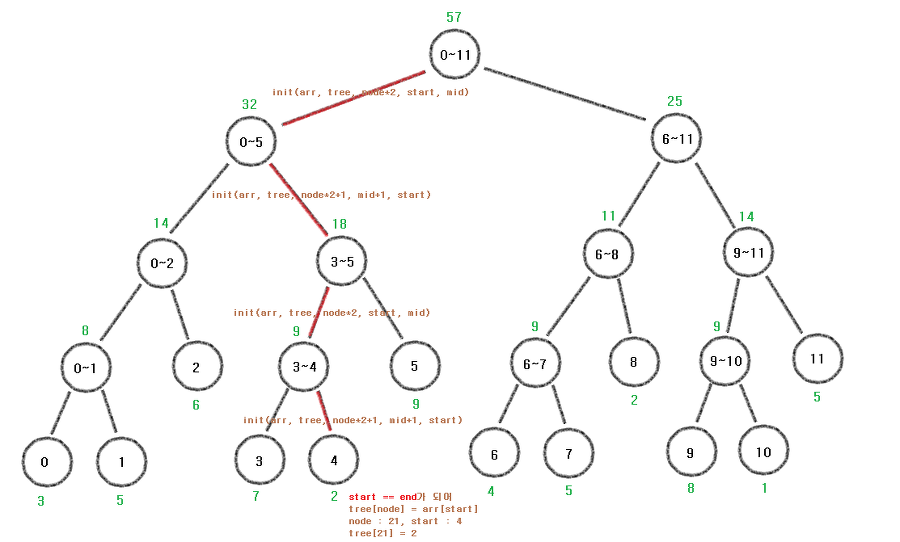
이렇게 init함수를 재귀를 통해 반복하면 위의 그림이 완성된다.
2. 갱신 과정(update)
void update(vector<ll> &tree, int node, int start, int end, int index, ll diff)
{
if (!(start <= index && index <= end))
return;
tree[node] += diff;
if(start != end)
{
int mid = (start + end) / 2;
update(tree, node * 2, start, mid, index, diff);
update(tree, node * 2 + 1, mid + 1, end, index, diff);
}
}
// This source code Copyright belongs to Crocus
// If you want to see more? click here >>
Crocus
인자
void update(vector<ll> &tree, int node, int start, int end, int index, ll diff)
- tree 벡터(배열)
- node번호
- start
- end
- 바꾸고자하는 인덱스 번호(바꾸고자 하는 노드 번호)
- 차이
start와 end사이에 index가 있지 않다면?
if (!(start <= index && index <= end))
return;return 해버린다.
그림으로 확인해보면 다음과 같다.
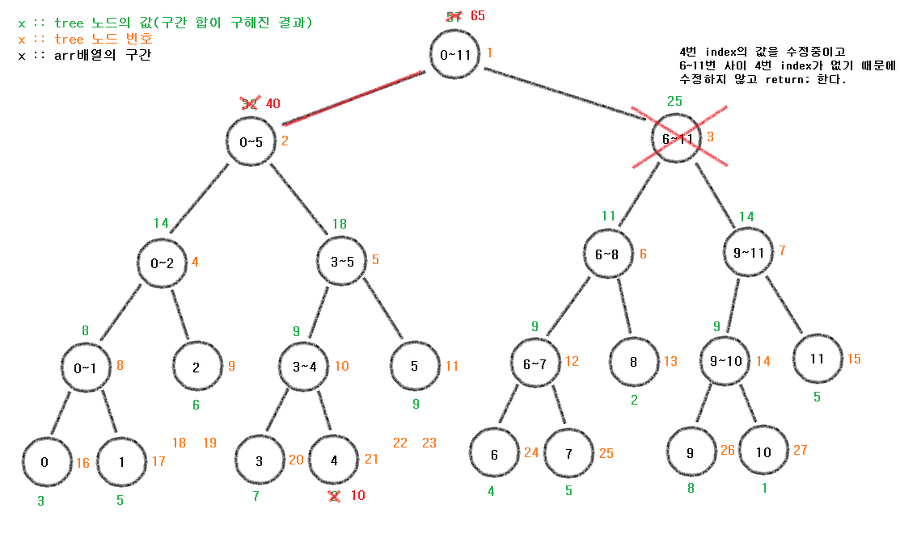
현재 세그먼트 트리 기준으로 21번 노드의 값을 2에서 10으로 변경하려 한다.
void update(vector<ll> &tree, int node, int start, int end, int index, ll diff)update(tree, 1, 0, 11, 4, 8)
우리는 node를 1번 노드부터 시작할 것이고,
start는 0번, end는 11번,
index는 4번, diff는 10 - 2를뺀 8이다.
if (!(start <= index && index <= end))
return;현재 index :: 4는 0 <= 4 <= 11이다.
따라서 if문에는 걸리지 않고 넘어간다.
tree[node] += diff;
if(start != end)
{
int mid = (start + end) / 2;
update(tree, node * 2, start, mid, index, diff);
update(tree, node * 2 + 1, mid + 1, end, index, diff);
}tree[node] += diff;
tree[1] += 8;
이 말은 무엇이냐면, 아까 2에서 10으로 값이 변했을 때 변화값이 8이니
전체 구간 합(tree[1])도 8만큼
값을 증가시켜야 한다는 말이다.
이제 start != end이니 각 update로 다시 들어가보자.
update(tree, 2, 0, 5, 4, 8);
update(tree, 3, 6, 11, 4, 8);
으로 받아지게 될 것이다.
위의 update를 타고 들어가면
start = 0, end = 5가 되어있어서
if (!(start <= index && index <= end))
return;0 <= 4 <= 5라 걸리지 않고 tree[node] += diff를 하게 되지만,
아래 update는 타고 들어가면
start = 6, end = 11이어서
6<= 4 <= 11에 걸리게 된다.
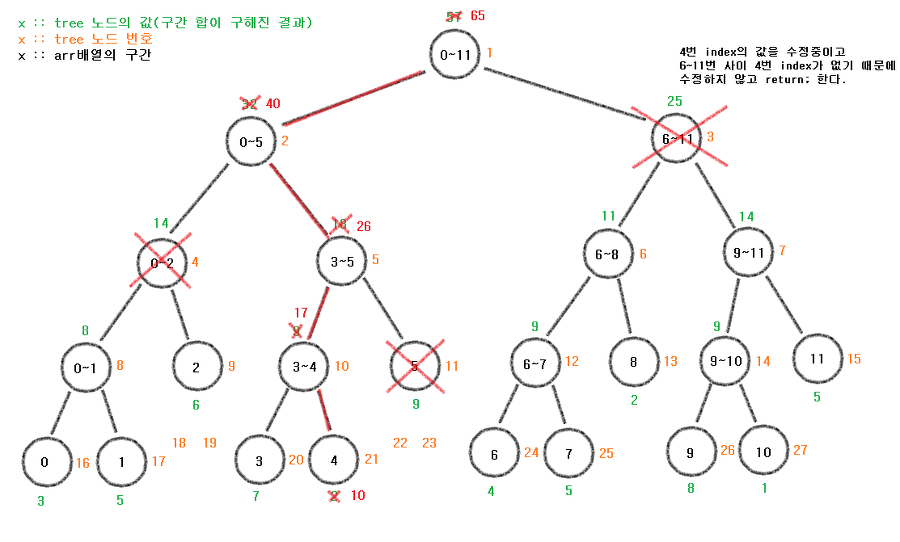
이 과정이 무얼 의미하는지 그림을 통해 보자
결국 update과정을 모두 마치게 되면 다음과 같은 모습이 나타나게 된다.(빨간색 값으로 update가 되었다.)
3. 합 과정(sum)
합을 구하는 과정은 4가지 경우로 나눌 수 있다.
1. [left, right]와 [start, end]가 겹치지 않는 경우
-> 즉 구간 합을 구하고자 하는 범위와
아예 상관이 없는 경우
:: if(left > end || right < start)로
표현 할 수 있다.
2. [left, right]가 [start, end]를 완전히 포함하는 경우
-> 즉, 구하고자 하는 구간 합 구간에 포함되는 경우
:: if(left <= start && end <= right)로
표현할 수 있다.
3. [start, end]가 [left, right]를 완전히 포함하는 경우
-> 즉, 구하고자 하는 구간 합 범위보다는 크게 있지만
그 내부에 구하고자 하는 구간 합 범위가 있는 경우
:: return sum(tree, node*2, start, mid, left, right) + sum(tree, node*2+1, mid+1, end, left, right)로 표현할 수 있다.
4. [left, right]와 [start, end]가 겹쳐져 있는 경우(1,2,3을 제외한 나머지 경우)
-> 즉, left <= start <= right <= end같은 방식인 경우
:: return sum(tree, node*2, start, mid, left, right) + sum(tree, node*2+1, mid+1, end, left, right)로 표현할 수 있다.
결론적으로 3,4는 재탐색을 해야하고 1,2,3,4를 합치면 아래 코드처럼 표현할 수 있다.
ll sum(vector<ll> &tree, int node, int start, int end, int left, int right)
{
if (left > end || right < start)
return 0;
if (left <= start && end <= right)
return tree[node];
int mid = (start + end) / 2;
return sum(tree, node * 2, start, mid, left, right) + sum(tree, node*2+1, mid+1, end, left, right);
}
// This source code Copyright belongs to Crocus
// If you want to see more? click here >>인자
- tree
- node번호
- start번호
- end번호
- left
- right
여기서 left와 right는
구간 left~right의 합을 구해달라는 의미이다.
합 과정 또한 그림으로 확인해보자.
다음과 같이 8~11의 구간합을 구하고 싶다고 가정한다.
이때 left는 8, right는 11이 될 것이다.
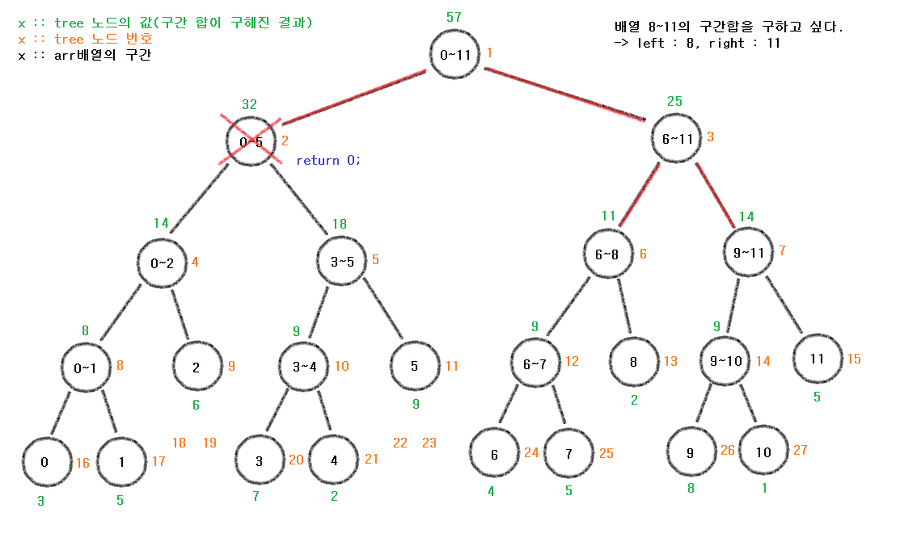
루트노드부터 관찰해 보자.
if (left > end || right < start)
return 0;
if(8 > 11 || 11 < 0) 이니 둘다 만족하지 않는다.
따라서 다음 단계로 간다.
if (left <= start && end <= right)
return tree[node];
if(8 <= 0 && 11 <= 11) 이니
다음 단계로 간다.
int mid = (start + end) / 2;
return sum(tree, node * 2, start, mid, left, right) + sum(tree, node*2+1, mid+1, end, left, right);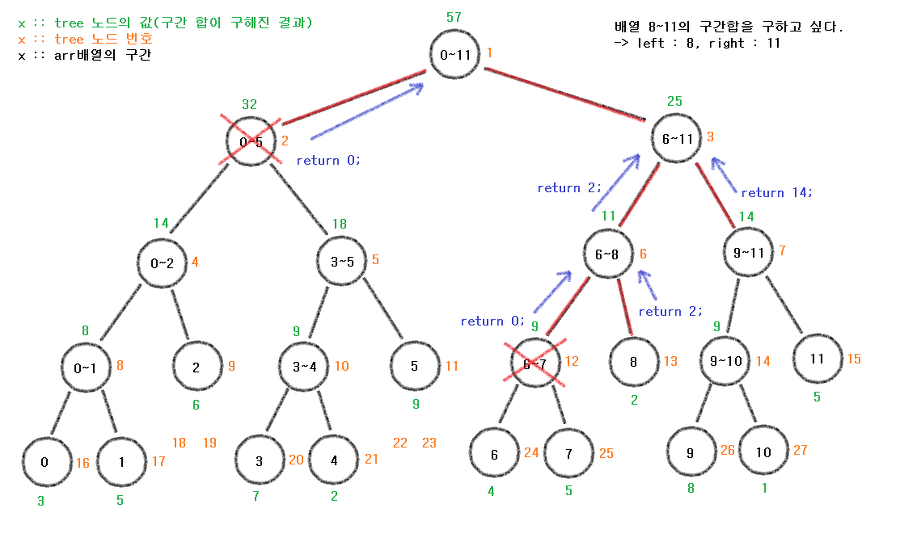
이제 2번 노드(arr 0~5번 배열의 구간합을 가진 노드)와
3번 노드(arr 6~11번 배열의 구간합을 가진 노드)를
관찰해야 한다.
2번 노드
if (left > end || right < start)
return 0;left(8)는 end(5)보다 크다. 그리고 right(11)은 start(0)보다 크다.
따라서 left > end가 만족하므로 return 0;을 해버린다.
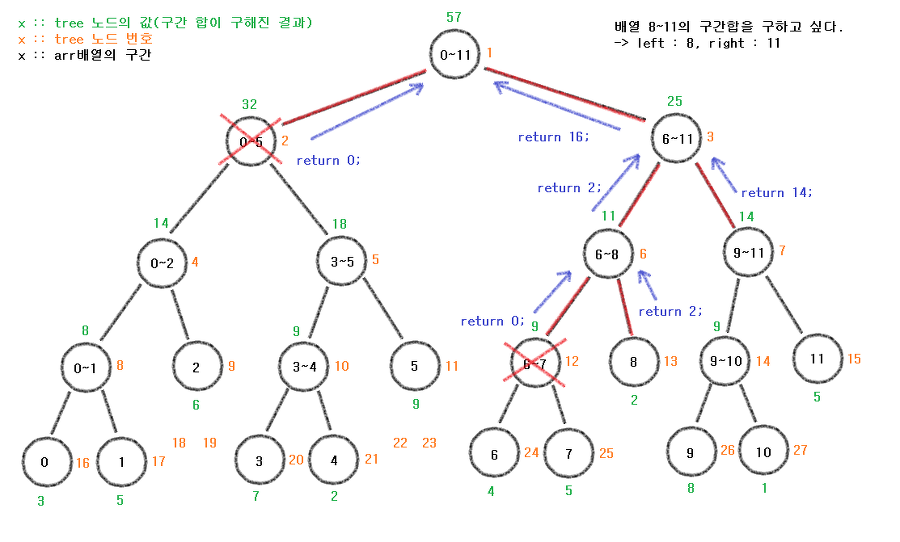
3번 노드
if (left > end || right < start)
return 0;
해당사항이 없으니 넘어간다.
if (left <= start && end <= right)
return tree[node];left = 8
start = 6
right = 11
end = 11이다.
if(0 && 1)이니 넘어간다.
int mid = (start + end) / 2;
return sum(tree, node * 2, start, mid, left, right) + sum(tree, node*2+1, mid+1, end, left, right);
위의 코드에 의해 다음과 같이 그림이 생성된다.
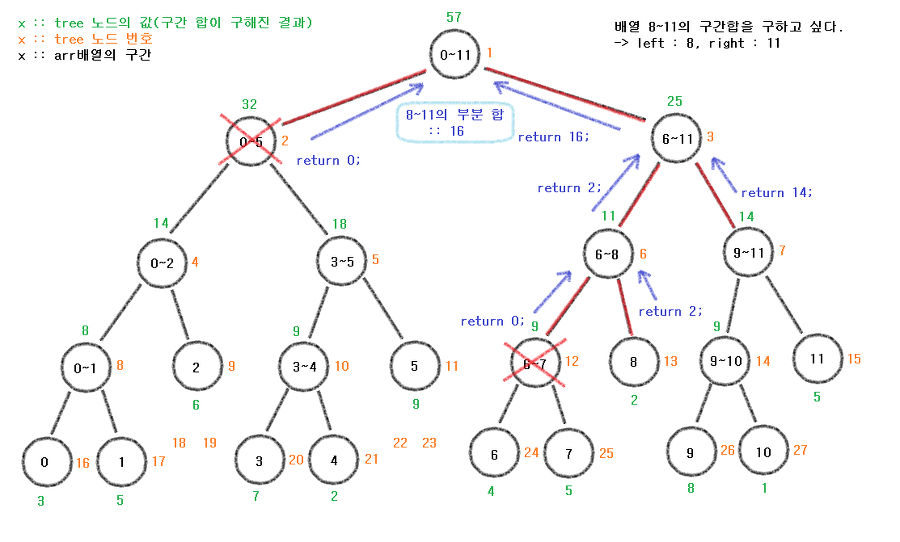
이러한 방식으로 모두 마무리 짓게 되면 다음과 같이 형성된다.
최종적으로
0~5는 관련없으므로 return 0;
6~7도 관련 없으므로 return 0;
8은 if(left <= start && end <= right)이므로 return 2; ((즉, 구간에 포함되는 노드라는 의미))
9~11또한 8처럼 구간에 포함되는 노드이기에 return 14;
return sum() + sum();이었으니 또 그 위 단계로 return 해준다.
최종적으로 16이 return 된다.
💡 참고 포스팅
세그먼트 트리(Segment Tree)
[ 세그먼트 트리(Segment Tree) ] 개념과 구현방법 (C++)
