[백준] 11266번: 단절점

https://www.acmicpc.net/problem/11266

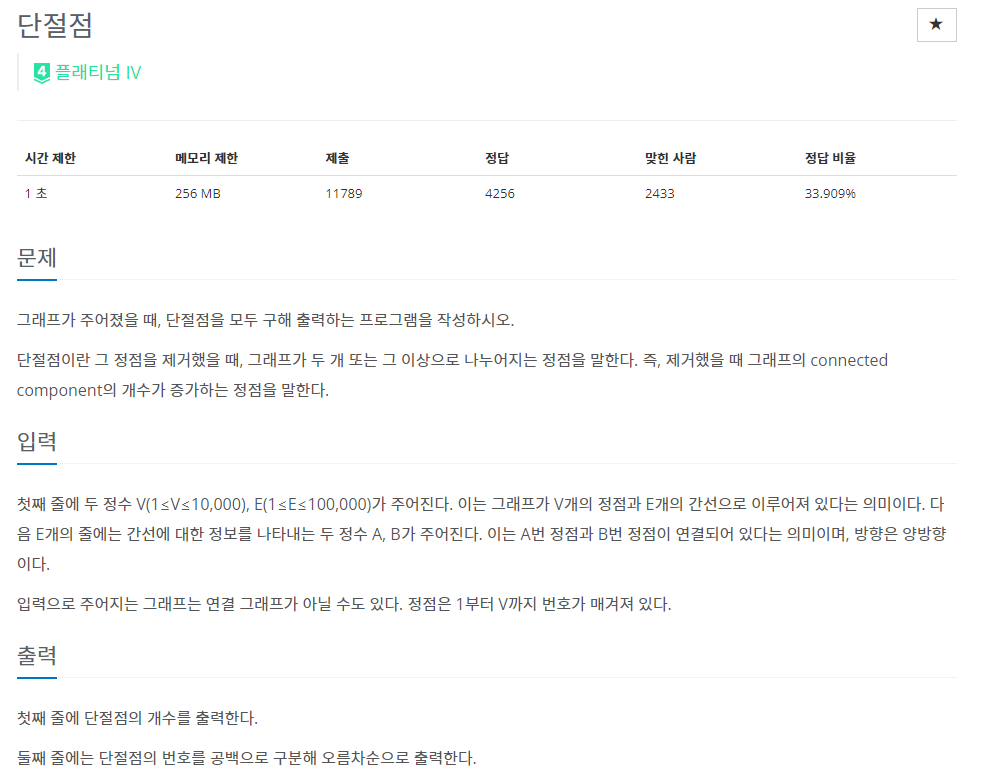
문제

알고리즘 접근 방법

1. 주어진 그래프에 대해서 방문하지 않은 정점을 시작으로
   dfs 탐색을 수행하여 order를 저장한다.
2. dfs함수는 하나의 정점에 연결된 다른 정점들을 탐색하면서 low를 리턴한다.
3. 자신과 연결된 정점에 대해서 dfs탐색을 수행 후
   반환된 low값과 자신의 방문 order를 비교하여 단절점 여부를 확인한다.

• 현재 정점이 시작 정점(루트 노드)이 아니면서
  자신과 연결된 정점의 dfs탐색 후 반환한 low값이
  자신의 방문 order보다 크거나 같다면
  그러한 점이 한 개라도 존재한다면 현재 정점은 단절점이다.
• 현재 정점이 시작 정점(루트 노드)이면서
  자신과 연결된 자식 트리의 개수가 2개 이상이라면
  현재 정점은 단절점이다.

단절점 판단 : 부모와 자식이 나를 통해 연결이 되어 있는가!!
부모정보 & 자식정보 수집해서
내가 필요가 있는지, 없는지를 판단한다.

풀이

#include <iostream>
#include <stack>
#include <vector>
using namespace std;

// A. 단절점

int V, E, a, b; // 그래프가 V개의 정점과 E개의 간선으로 이루어져 있다
vector<int> AL[10001]; // 인접 리스트

int visit_order[10001]; // 방문 순서 저장됨. 미방문 = 0 
int cut_vertex[10001]; // 각 정점이 단절점인지의 여부 저장
vector<int> result; // 단절점 정보

int order = 0; // 방문 순서 

int dfs(int curr, int parent){ // 현재 노드의 low 반환해야 함.
    visit_order[curr] = ++order; // 방문 순서 저장

    // 내 부모에게 넘겨줄 low (현재 나의 return 값) 저장하는 변수
    // 나와 연결된 점을 방문했을 때 방문한 연결 점이 방문했던 점들 중 order가 가장 빠름. 
    int min_order = visit_order[curr]; 
    
    // child의 개수 저장
    int child = 0;

    for (int next : AL[curr]){
        if (next == parent) continue; // 부모 노드 인 경우 pass
        if (visit_order[next] > 0){ // 다음 정점이 이미 방문한 정점일 경우

            // min order 갱신

            min_order = (visit_order[next] < min_order)? visit_order[next] : min_order;
        }
        else{ // 다음 정점이 아직 미방문인 경우
            ++child;
            int low = dfs(next, curr);

            if (parent != 0 && visit_order[curr] <= low) cut_vertex[curr] = 1;
            
            min_order = (low < min_order)? low : min_order;
        }
    }
	
     // 루트노드일경우 자식이 2개 이상이면 단절점.
    if (parent == 0 && child >= 2) cut_vertex[curr] = 1;
    return min_order;
}

// 단절점 판단 : 부모와 자식이 나를 통해 연결이 되어 있는가!!


int main(){

    // input
    cin >> V >> E;

    for(int i=0; i<E; i++){
        cin >> a >> b;

        AL[a].push_back(b);
        AL[b].push_back(a);
    }

    // processing

    for(int i=1; i<=V; i++){ 
        // 부모노드 같이 들고 다니면서 저장
        if (visit_order[i] == 0) dfs(i, 0);
    }

    for(int i=1; i<=V; i++){
        if (cut_vertex[i]) result.push_back(i);
    }

    // output


    // 첫째 줄에 단절점의 개수를 출력한다.
    cout << result.size() << '\n';

    // 둘째 줄에는 단절점의 번호를 공백으로 구분해 오름차순으로 출력한다.
    for(int i : result){
        cout << i << " ";
    }
    return 0;
}

Core 코드

int dfs(int curr, int parent) {
  VisitOrder[curr] = ++order; // 방문 order 저장

  // 내 부모에게 넘겨줄 low (현재 나의 return 값) 저장하는 변수.
  // 나와 연결된 점을 방문했을 때 방문한 연결 점이 방문(시도)했던 점들 중
  // order가 가장 빠른 것.
  int minOrder = VisitOrder[curr];

  // child 의 개수를 저장
  int child = 0;

  // 다음 방문 예정인 점을 탐색
  for (int next : AL[curr]) {
    if (next == parent) continue; // 부모노드인 경우 방문 시도를 하지 않는다.

    // 부모 노드가 아닌 경우 next에 방문 시도를 해 본다.
    if (VisitOrder[next] > 0) { // next 가 이미 방문을 한 노드인 경우
      // 이 부분 집중!!!!!!!
      // DST 의 관점에서 보면 이러한 노드들은 curr의 조상인 경우 외엔 존재할 수 없다.
      // 다시 말해, next 노드는 현재 dfs 작업이 끝난 상태가 아니므로, next 노드
      // 에서의 유효한 order 값은 VisitOrder[next] 가 유일하다.
      minOrder = VisitOrder[next] < minOrder ? VisitOrder[next] : minOrder;
    }
    else { // next 가 미 방문 상태인 경우
      ++child;
      int low = dfs(next, curr);

      if (parent != 0 && VisitOrder[curr] <= low) CutVertex[curr] = 1;

      minOrder = low < minOrder ? low : minOrder;
    }
  }
  if (parent == 0 && child >= 2) CutVertex[curr] = 1;
  return minOrder;
}

// 여기서 minOrder 가 무엇이고, low 가 무엇인지를 확실히 구분할 줄 알아야 합니다.
// dfs 호출 바깥에서 로직을 완성하는 방법은 직접 생각하여 프로그래밍해 보시기 바랍니다.
// 물론 위에 공유 드린 dfs 코드도 직접 손으로 따라 쳐 보시면서 익히시는 것을 권장합니다.

정리

흐아 . . . 다시 풀어봐..