https://www.acmicpc.net/problem/1256
문제
알고리즘 접근 방법
(1) 첫 문자열이 'a' 혹은 'z'인 문자열의 수
길기아 N+M이고 'a'의 개수가 N개, 'z'의 개수가 M개인 문자열은
첫 문자가 'a'인 경우와 'z'인 경우밖에 없다.
첫 문자가 'a'인 경우 첫 문자가 'a'로 결정되었으므로 총 길이 N+M-1 개 중 M개가 'z'인 문자열의 수와 같다. 즉, 첫 문자가 'a'인 문자열의 수는 N+M-1_C_M 이다.
첫 문자가 'z'인 경우 첫 문자가 'z'로 결정되었으므로 총 길이 N+M-1 개 중 M-1개가 'z'인 문자열의 수와 같다. 즉, 첫 문자가 'z'인 문자열의 수는 N+M-1_C_M-1 이다.
위의 내용을 정리하면 길이가 N+M이고 'z'의 개수가 M개인 문자열의 수는 다음과 같다.
=> N+M_C_M = N+M-1_C_M + N+M-1_C_M-1
(2) K번째 문자열 찾기
앞에서 정리한 내용으로 사전에 들어갈 문자열은 첫문자가 'a'인 경우와 'z'인 경우의 합으로 나타낼 수 있으며 수식으로 나타내면 N+M_C_M = N+M-1_C_M + N+M-1_C_M-1 이다. 또한 문자열은 사전 순으로 나타낼 것이므로 순서적으로 첫 문자가 'a'인 모든 비트문자열은 첫 문자가 'z'인 문자열 앞에 있다.
만약 K번째 문자열의 첫 문자가 'a'라면 K <= N+M-1_C_M 임을 만족해야 한다.
K가 첫 문자를 'a'로 만들 수 있는 문자열의 수보다는 작거나 같아야 하기 때문이다.
이 성질을 이용하면 첫 문자를 결정할 수 있으며, 두 번째 문자를 결정하는 문제는 전체 길이가 N+M-1이고 'z'의 개수가 M개인 문제로 놓고 똑같은 원리로 풀 수 있다.
ex. N=2 M=3 K=7

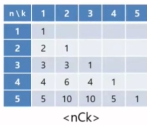
가장 첫 문자가 'a'인 문자열의 수는 4_C_3이므로 4개가 있다는 것을 쉽게 구할 수 있다.
우리가 찾는 K는 7이므로 첫 문자는 'z'임을 알 수 있다.
첫 문자가 'z'로 결정되면, 첫 문자가 'a'인 문자열을 건너뛰고 찾게 되므로 첫 문자가 'z'로 시작하는 문자열 중에 3번째인 문자열을 찾으면 된다.
즉, 두번째 문자를 결정하는 문제는 전체 길이가 4이고 M이 2인 문자열 중 K가 3인 문제를 풀는 것과 동일한 문제가 된다.
풀이
아직 푸는 중
