문제
https://www.acmicpc.net/problem/1967
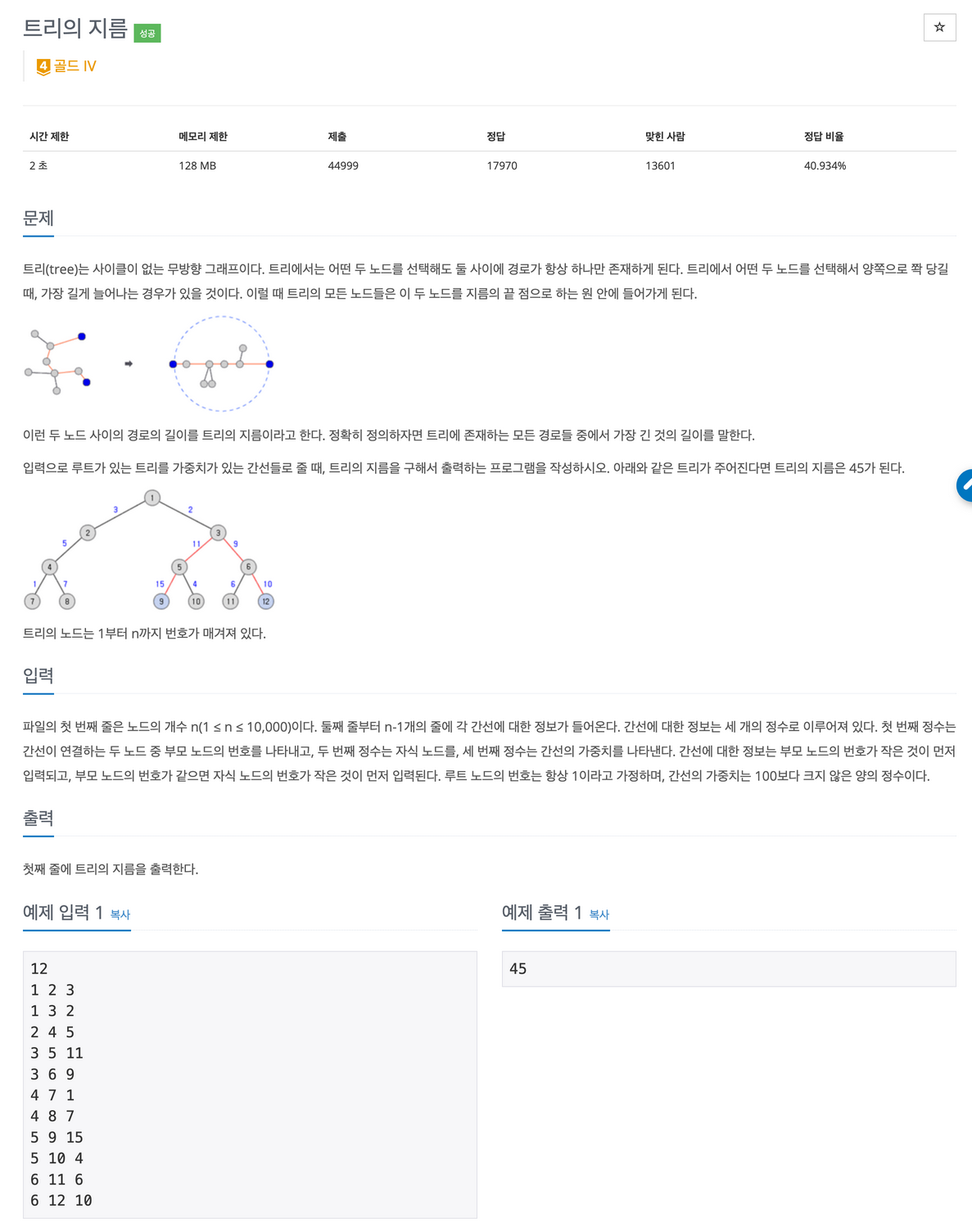
접근 방법
1번째, 2번째 시도
- 리프 노드들의 리스트를 구한다
- 리프노드 ~ 리프노드 사이 거리 중 가장 긴 거리를 구한다.
- 이 때 lca(최소공통조상) 을 이용한다.
3번째, 4번째 시도
- 트리에서 임의의 정점 x(나는 root로 했음)를 잡는다.
- 정점 x에서 가장 먼 정점 y를 찾는다.
- 정점 y에서 가장 먼 정점 z를 찾는다.
트리의 지름은 정점 y와 정점 z를 연결하는 경로다.
증명 : https://blog.myungwoo.kr/112 [PS 이야기:티스토리]
풀이
1번째 시도
#include <iostream>
#include <vector>
#include <algorithm>
#include <stack>
#define MAX 10004
using namespace std;
vector<int> childs[MAX];
int parents[MAX];
int weights[MAX][MAX]; // 부모 - 자식 10000 * 10000 * 4byte > 128MB
int levels[MAX];
void fastIO() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
}
void input(int &n, vector<pair<pair<int, int>, int>> &edges) {
cin >> n;
int parent, child, weight;
for(int i=0; i<n-1; i++) {
cin >> parent >> child >> weight;
edges.push_back({{parent, child}, weight});
}
}
int lca(int a, int b) {
// a를 더 level이 높은 정점으로 맞춘다.
if (levels[a] < levels[b]) swap(a, b);
// 두 정점의 level을 같게 만들기
while (levels[a] != levels[b]) {
a = parents[a];
}
// 가리키는 정점이 같아질 때까지 거슬러 올라가기
while (a != b) {
a = parents[a];
b = parents[b];
}
return a;
}
int getLength(int start, int root) {
int length = 0;
while(start != root) {
length += weights[parents[start]][start];
start = parents[start];
}
return length;
}
int solve(int &n, vector<pair<pair<int, int>, int>> &edges) {
vector<int> leafNodes;
for(auto edge : edges) {
int parent = edge.first.first;
int child = edge.first.second;
int weight = edge.second;
childs[parent].push_back(child);
parents[child] = parent;
weights[parent][child] = weight;
}
// 리프 노드 리스트 만들기
for(int i=1; i<=n; i++) {
if (childs[i].size() == 0) {
leafNodes.push_back(i);
}
}
// levels 설정하기
stack<pair<int, int>> s;
s.push({1, 0}); // 1노드, 레벨 0
while(!s.empty()) {
pair<int, int> curr = s.top();
int node = curr.first;
int level = curr.second;
levels[node] = level;
s.pop();
for(int child : childs[node]) {
s.push({child, level+1});
}
}
int answer = 0;
// 단말 to 단말
for(int i=0; i<leafNodes.size(); i++) {
for(int j=i+1; j<leafNodes.size(); j++) {
int startNode = leafNodes[i];
int endNode = leafNodes[j];
int parent = parents[startNode];
// 최소 공통 조상 구하기
int lcaNode = lca(startNode, endNode);
// startNode ~ 최소 공통 조상 + 최소 공통 조상 ~ end 거리
int length = getLength(startNode, lcaNode) + getLength(endNode, lcaNode);
answer = max(answer, length);
}
}
return answer;
}
void output(int answer) {
cout << answer << '\n';
}
int main() {
int n;
vector<pair<pair<int, int>, int>> edges; // {부모 - 노드, 가중치} 의 리스트
fastIO();
input(n, edges);
output(solve(n, edges));
return 0;
}결과
메모리 초과
int weights[MAX][MAX]; // 부모 - 자식 10000 * 10000 * 4byte > 128MB2번째 시도
#include <iostream>
#include <vector>
#include <algorithm>
#include <stack>
#include <unordered_map>
#define MAX 10004
using namespace std;
int parents[MAX];
int levels[MAX];
unordered_map<int, vector<pair<int, int>>> childs; // 자식 - 가중치
void fastIO() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
}
void input(int &n, vector<pair<pair<int, int>, int>> &edges) {
cin >> n;
int parent, child, weight;
for(int i=0; i<n-1; i++) {
cin >> parent >> child >> weight;
edges.push_back({{parent, child}, weight});
}
}
int lca(int a, int b) {
// a를 더 level이 높은 정점으로 맞춘다.
if (levels[a] < levels[b]) swap(a, b);
// 두 정점의 level을 같게 만들기
while (levels[a] != levels[b]) {
a = parents[a];
}
// 가리키는 정점이 같아질 때까지 거슬러 올라가기
while (a != b) {
a = parents[a];
b = parents[b];
}
return a;
}
int getWeight(int parent, int child) {
for(auto i : childs[parent]) {
if (i.first == child) return i.second;
}
return 0;
}
int getLength(int start, int root) {
int length = 0;
while(start != root) {
length += getWeight(parents[start], start);
start = parents[start];
}
return length;
}
int solve(int &n, vector<pair<pair<int, int>, int>> &edges) {
vector<int> leafNodes;
for(auto edge : edges) {
int parent = edge.first.first;
int child = edge.first.second;
int weight = edge.second;
childs[parent].push_back({child, weight});
parents[child] = parent;
}
// 리프 노드 리스트 만들기
for(int i=1; i<=n; i++) {
if (childs[i].size() == 0) {
leafNodes.push_back(i);
}
}
// levels 설정하기
stack<pair<int, int>> s;
s.push({1, 0}); // 1노드, 레벨 0
while(!s.empty()) {
pair<int, int> curr = s.top();
int node = curr.first;
int level = curr.second;
levels[node] = level;
s.pop();
if (childs.find(node) != childs.end()) {
for(auto child : childs[node]) {
s.push({child.first, level+1});
}
}
}
int answer = 0;
// 단말 to 단말
for(int i=0; i<leafNodes.size(); i++) {
for(int j=i+1; j<leafNodes.size(); j++) {
int startNode = leafNodes[i];
int endNode = leafNodes[j];
int parent = parents[startNode];
// 최소 공통 조상 구하기
int lcaNode = lca(startNode, endNode);
// startNode ~ 최소 공통 조상 + 최소 공통 조상 ~ end 거리
int length = getLength(startNode, lcaNode) + getLength(endNode, lcaNode);
answer = max(answer, length);
}
}
return answer;
}
void output(int answer) {
cout << answer << '\n';
}
int main() {
int n;
vector<pair<pair<int, int>, int>> edges; // {부모 - 노드, 가중치} 의 리스트
fastIO();
input(n, edges);
output(solve(n, edges));
return 0;
}결과
시간 초과
모든 리프 노드에서 전부 시작하면 시간초과 ..
트리 지름 구하는 방법 이용하여 수정
아무 점이나 잡고(루트), 이 점에서 가장 거리가 먼 점 t 를 잡는다. t에서 가장 거리가 먼점 u 를 찾는다
3번째 시도
#include <iostream>
#include <vector>
#include <algorithm>
#include <stack>
#include <unordered_map>
#define MAX 10004
using namespace std;
int parents[MAX];
int levels[MAX];
unordered_map<int, vector<pair<int, int>>> childs; // 자식 - 가중치
void fastIO() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
}
void input(int &n, vector<pair<pair<int, int>, int>> &edges) {
cin >> n;
int parent, child, weight;
for(int i=0; i<n-1; i++) {
cin >> parent >> child >> weight;
edges.push_back({{parent, child}, weight});
}
}
int lca(int a, int b) {
// a를 더 level이 높은 정점으로 맞춘다.
if (levels[a] < levels[b]) swap(a, b);
// 두 정점의 level을 같게 만들기
while (levels[a] != levels[b]) {
a = parents[a];
}
// 가리키는 정점이 같아질 때까지 거슬러 올라가기
while (a != b) {
a = parents[a];
b = parents[b];
}
return a;
}
int getWeight(int parent, int child) {
for(auto i : childs[parent]) {
if (i.first == child) return i.second;
}
return 0;
}
int getLength(int start, int root) {
int length = 0;
while(start != root) {
length += getWeight(parents[start], start);
start = parents[start];
}
return length;
}
int solve(int &n, vector<pair<pair<int, int>, int>> &edges) {
vector<int> leafNodes;
int root = 1;
for(auto edge : edges) {
int parent = edge.first.first;
int child = edge.first.second;
int weight = edge.second;
childs[parent].push_back({child, weight});
parents[child] = parent;
}
// 리프 노드 리스트 만들기
for(int i=1; i<=n; i++) {
if (childs[i].size() == 0) {
leafNodes.push_back(i);
}
}
// levels 설정하기
stack<pair<int, int>> s;
s.push({root, 0}); // 루트 노드, 레벨 0
while(!s.empty()) {
pair<int, int> curr = s.top();
int node = curr.first;
int level = curr.second;
levels[node] = level;
s.pop();
if (childs.find(node) != childs.end()) {
for(auto child : childs[node]) {
s.push({child.first, level+1});
}
}
}
int rootToLeaf = 0;
int t;
// 아무 점이나 잡고(루트), 이 점에서 가장 거리가 먼 점 t 를 잡는다
for(int i=0; i<leafNodes.size(); i++) {
int length = getLength(leafNodes[i], root);
if (rootToLeaf < length) {
rootToLeaf = length; // t ~ root
t = leafNodes[i];
}
}
int answer = 0;
// t에서 가장 거리가 먼점 u 를 찾는다
for(int i=0; i<leafNodes.size(); i++) {
int u = leafNodes[i];
if (t == u)
continue;
int lcaNode = lca(t, u);
int length = getLength(t, lcaNode) + getLength(u, lcaNode);
answer = max(answer, length);
}
return answer;
}
void output(int answer) {
cout << answer << '\n';
}
int main() {
int n;
vector<pair<pair<int, int>, int>> edges; // {부모 - 노드, 가중치} 의 리스트
fastIO();
input(n, edges);
output(solve(n, edges));
return 0;
}결과
32% 틀렸습니다
n = 1일 경우 -> 0
"어떤 트리에서 경로의 길이가 최대가 될 때 두 노드는 모두 leaf노드이다." 라고 하셨는데, 이게 맞지 않는 경우가 있습니다.
바로 루트의 자식이 1개 뿐일 때 입니다.
예를 들면 일자모양인 트리가 있겠죠.
이런 경우에는 루트도 비교후보 중 하나로 삼아야 합니다.
4차 시도
#include <iostream>
#include <vector>
#include <algorithm>
#include <stack>
#include <unordered_map>
#define MAX 10004
using namespace std;
int parents[MAX];
int levels[MAX];
unordered_map<int, vector<pair<int, int>>> childs; // 자식 - 가중치
void fastIO() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
}
void input(int &n, vector<pair<pair<int, int>, int>> &edges) {
cin >> n;
int parent, child, weight;
for(int i=0; i<n-1; i++) {
cin >> parent >> child >> weight;
edges.push_back({{parent, child}, weight});
}
}
int lca(int a, int b) {
// a를 더 level이 높은 정점으로 맞춘다.
if (levels[a] < levels[b]) swap(a, b);
// 두 정점의 level을 같게 만들기
while (levels[a] != levels[b]) {
a = parents[a];
}
// 가리키는 정점이 같아질 때까지 거슬러 올라가기
while (a != b) {
a = parents[a];
b = parents[b];
}
return a;
}
int getWeight(int parent, int child) {
for(auto i : childs[parent]) {
if (i.first == child) return i.second;
}
return 0;
}
int getLength(int start, int root) {
int length = 0;
while(start != root) {
length += getWeight(parents[start], start);
start = parents[start];
}
return length;
}
int solve(int &n, vector<pair<pair<int, int>, int>> &edges) {
if (n == 1) {
return 0;
}
vector<int> leafNodes;
int root = 1;
for(auto edge : edges) {
int parent = edge.first.first;
int child = edge.first.second;
int weight = edge.second;
childs[parent].push_back({child, weight});
parents[child] = parent;
}
// 리프 노드 리스트 만들기
for(int i=1; i<=n; i++) {
if (childs[i].size() == 0) {
leafNodes.push_back(i);
}
}
// levels 설정하기
stack<pair<int, int>> s;
s.push({root, 0}); // 루트 노드, 레벨 0
while(!s.empty()) {
pair<int, int> curr = s.top();
int node = curr.first;
int level = curr.second;
levels[node] = level;
s.pop();
if (childs.find(node) != childs.end()) {
for(auto child : childs[node]) {
s.push({child.first, level+1});
}
}
}
int rootToLeaf = 0;
int t;
// 아무 점이나 잡고(루트), 이 점에서 가장 거리가 먼 점 t 를 잡는다
for(int i=0; i<leafNodes.size(); i++) {
int length = getLength(leafNodes[i], root);
if (rootToLeaf < length) {
rootToLeaf = length; // t ~ root
t = leafNodes[i];
}
}
int answer = 0;
// t에서 가장 거리가 먼점 u 를 찾는다
for(int i=0; i<leafNodes.size(); i++) {
int u = leafNodes[i];
if (t == u)
continue;
int lcaNode = lca(t, u);
int length = getLength(t, lcaNode) + getLength(u, lcaNode);
answer = max(answer, length);
}
// root 노드와도 비교한다.
answer = max(answer, getLength(t, root));
return answer;
}
void output(int answer) {
cout << answer << '\n';
}
int main() {
int n;
vector<pair<pair<int, int>, int>> edges; // {부모 - 노드, 가중치} 의 리스트
fastIO();
input(n, edges);
output(solve(n, edges));
return 0;
}
결과
성공!!
정리
2시간동안 푼 것 같다...
메모리랑 시간 복잡도 계산은 역시 중요하다
풀이가 생각났더라도 주석으로 흐름 쓰고, 필요한 변수들 메모리 계산해보고 시간 계산 해보기
다른 반례들을 잘 생각해보고 고려하기
참고
https://www.acmicpc.net/board/view/132816
https://www.acmicpc.net/board/view/13728
https://www.acmicpc.net/board/view/8114
https://blog.myungwoo.kr/112
