[백준] 2609번: 최대공약수와 최소공배수

https://www.acmicpc.net/problem/2609

문제

알고리즘 접근 방법

최대공약수 GCD(Greatest Common Divisor)
최대공약수는 두 자연수의 공통된 약수 중 가장 큰 수를 의미한다.
ex) 72 와 30의 최대공약수는 6이다.

최소공배수 LCM(Least Common Multiple)
최소공배수는 두 자연수의 공통된 배수 중 가장 작은 수를 의미한다.
최소공배수 = 두 자연수의 곱 / 최대공약수
ex) 72 와 30의 최소공배수는 360이다.

2개의 자연수를 받아 최대공약수를 받기 위해
2부터 두 자연수 중 작은 자연수까지 모두 나누어보면서 가장 큰 공약수를 구할 수 있다.
위와 같은 방법으로 문제를 풀면
시간복잡도는 O(N)이 된다.

나쁜 방법은 아니지만 효율을 높이기 위해
유클리드 호제법 알고리즘을 사용하면
시간복잡도를 O(logN)으로 줄일 수 있다.

유클리드 호제법(Euclidean Algorithm)

2개의 자연수 a, b에 대해서
a를 b로 나눈 나머지를 r이라 하면 (단 a>b),
a와 b의 최대공약수는 b와 r의 최대공약수와 같다.

이 성질에 따라, b를 r로 나눈 나머지 r0를 구하고,
다시 r을 r0로 나눈 나머지를 구하는 과정을 반복하여
나머지가 0이 되었을 때 나누는 수가
a와 b의 최대공약수이다.

이는 명시적으로 기술된 가장 오래된 알고리즘으로서도
알려져 있으며, 기원전 300년경에 쓰인 유클리드의 <원론> 제7권, 명제 1부터 3까지에 해당한다

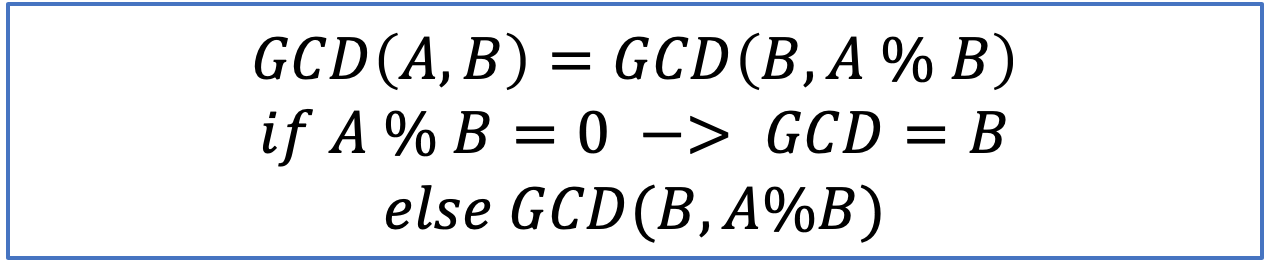
ex. 10과 8의 최대공약수?
1. a = 10, b = 8
GCD(10, 8) = GCD(8, 10%8) = GCD(8, 2)
2. a = 8, b = 2
8%2 = 0 -> GCD = 2

풀이

#include <iostream>

using namespace std;

int gcd(int a, int b){
    while(b > 0){
        int temp = b;
        b = a%b;
        a = temp;
    }

    return a;
}

int lcm(int a, int b){
    return (a*b)/gcd(a, b);
}

int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    int A, B;

    cin >> A >> B;

    cout << gcd(A, B) << '\n';
    cout << lcm(A, B) << '\n';
    return 0;
}

정리

유클리드 호제법 기억행~

💡 참고 포스팅

코드자몽님 블로그
Dreamy님 블로그