시간복잡도(time complexity)

---

입력 크기에 대해 어떠한 알고리즘이 실행되는데 걸리는 시간이며 주요 로직의 반복 횟수를 중점으로 측정됨

주어진 입력크기를 기반으로 어떠한 로직이 몇번 반복되었는가

빅오표기법(Big - O notation)

복잡도에 가장 많이 영향을 끼치는 항의 상수인자를 빼고 나머지 항을 없애서 복잡도를 나타내는 표기법

순서

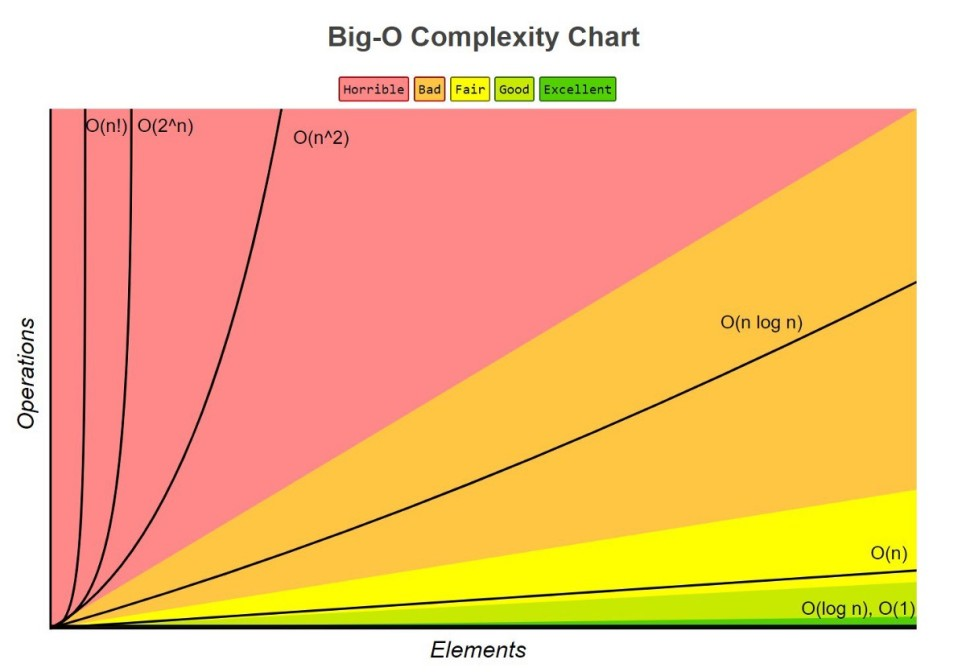
n! > 2^n > n^2 > nlogn > n > logn > 1

상수시간 시간복잡도 O(1)

입력 크기와 상관없이 일정한 시간 복잡도를 가지는 것

• 입력, 출력 : cin, cout, scanf, printf
• 곱하기, 나누기, 나머지연산, 빼기 : a[2] *= 2;
• 간단한 비교 if 문 : if (a[2]==2)
• 배열의 인덱스 참조 : int b = a[2];

예시

Q1.

#include<bits/stdc++.h>
using namespace std; 
int n;
int main(){
	cin >> n; 
	int a = 0;
	for(int i = 0; i < n; i++){
		for(int j = 0; j < i; j++){
			a += i + j; 
            // cnt++; -> 이런식으로 찍어보면서 구해도 됨
		}
	}
	cout << a << '\n';   
	return 0;
} 

O(n^2)

Q2.

#include<bits/stdc++.h>
using namespace std;  
int N, M;
void solve(int N, int M){
	int a = 1; 
	for (int i = 0; i < N; i++) {
		a *= i;  
	}
	for (int j = 0; j < M; j++) {
		a *= j;   
	}
	cout << a << "\n"; 
}

int main(){
	cin >> N >> M; 
	solve(N, M);    
	return 0;
} 

입력값이 여러가지일 경우
N따로 M따로..
중첩되지 않고 나열되어 있으면 +

O(N + M)

Q3.

#include<bits/stdc++.h>
using namespace std;  
int n, a[1004], cnt;
int go(int l, int r){ 
     // cnt++ -> 어려울 땐 디버깅 !
	if(l == r) return a[l];  
	int mid = (l + r) / 2; 
	int sum = go(l, mid) + go(mid + 1, r); 
	return sum;
}
int main(){
	cin >> n;  // 10
	for(int i = 1; i <= n; i++){
		a[i - 1] = i; 
	}
	int sum = go(0, n - 1);
	cout << sum << '\n';  // 45 
} 

재귀함수...

• n이 10일 때 cnt = 19
• n이 5일 때 cnt = 9
• 2n-1 인가~?

O(n)

• 점화식 세워서 할 수도 있음

Q4.

#include<bits/stdc++.h>
using namespace std;  

int N;

void solve(int N){
	int a = 0, i = N;
	while (i > 0) {
		a += i;
		i /= 2;
        cnt++; // 어려울 때 디버깅 
	} 
	cout << a << '\n';
    cout << cnt << '\n'; // 32 -> 6 / 16 -> 5 .. . => log2 (N + 1)
}

int main(){
	cin >> N; 
	solve(N);    
	return 0;
} 

log2 N

Q5.

재귀함수 = 메인로직이 몇번 호출되냐

1->3->9->27 ..
등비수열

(3^n -1) * (1/2) => O(3^n)

logic cnt
O(1) O(3^n) -> O(3^n)

[꿀팁] 어려우면?

• 함수 하나당 4번 호출 -> 4^n
• 함수 하나당 2번 호출 -> 2^n
  이라고 생각하세용