(연관규칙 알고리즘 )A-Priori: a multi-pass algorithm

메인메모리에서 frequent itemset을 찾는 알고리즘 입니다.

쉽게 이해 하기 위한

주어진 itemset I가 최소 s번 이상 나타난다고 가정해 봅시다. 그러면 itemset I의 부분집합 J는 최소 s번 이상 나타난다는 것을 의미합니다.

다시 말해, 만약 어떤 아이템 I가 최소 s개의 바스켓에 나타나지 않는다면, 즉 자주 등장하지 않는다면, I를 포함하는 어떤 pair도 s번 이상 나타날 수 없습니다.

예를 들어, {B}가 자주 등장하지 않는다면 {B,D}도 자주 등장하지 않습니다. 이는 {B}가 자주 등장하지 않으면 {B,D}와 같은 아이템셋은 전혀 자주 등장하지 않을 것이기 때문입니다.

따라서, 최소 s개의 바스켓이 자주 등장하지 않으면 {B},{BD}와 같은 아이템셋에 대한 탐색은 하지 않습니다. 이는 바로 가지치기를 의미합니다.

첫번째 pass:

첫 번째 패스에서는 각 바스켓을 순차적으로 읽으면서 메인 메모리에서 각 아이템이 몇 번 등장하는지를 셉니다. 이 과정에서는 singleton 아이템셋이 얼마나 자주 등장하는지를 확인합니다. 이때 필요한 메모리는 아이템의 개수만큼이 됩니다.

두번째 pass:

첫 번째 패스에서는 데이터를 다시 처음부터 쭉 읽게 되는데, 이때는 pass1에서 frequent하다고 판단한 아이템들의 쌍에 대해서만 count를 합니다. 즉, pass1에서 자주 등장하는 것으로 확인된 아이템들에 대해서만 pair를 만들어서 그 쌍을 카운트합니다.

메인 메모리 구조는 다음과 같습니다 , pass1에서는 메모리의 상단 영역에 각 개별 아이템의 카운트를 저장합니다. 이때 각 아이템의 카운트를 누적하고, 최소 s번 이상 등장하는 것으로 판단되는 frequent한 아이템들을 사용하여 가능한 모든 pair를 만듭니다. 그리고 이러한 pair의 카운트를 메모리 영역에서 세는 것이 pass2입니다.

빈발하게 나타나는 singleton item 과 pair의 count를 세는 방법

가장 많이 빈발하는 아이템을 찾은 후에는 이러한 빈발 아이템들을 기반으로 빈발 쌍의 후보를 골라냅니다. 이 후보 쌍들은 실제로 빈발한지를 카운트하여 확인하게 됩니다.

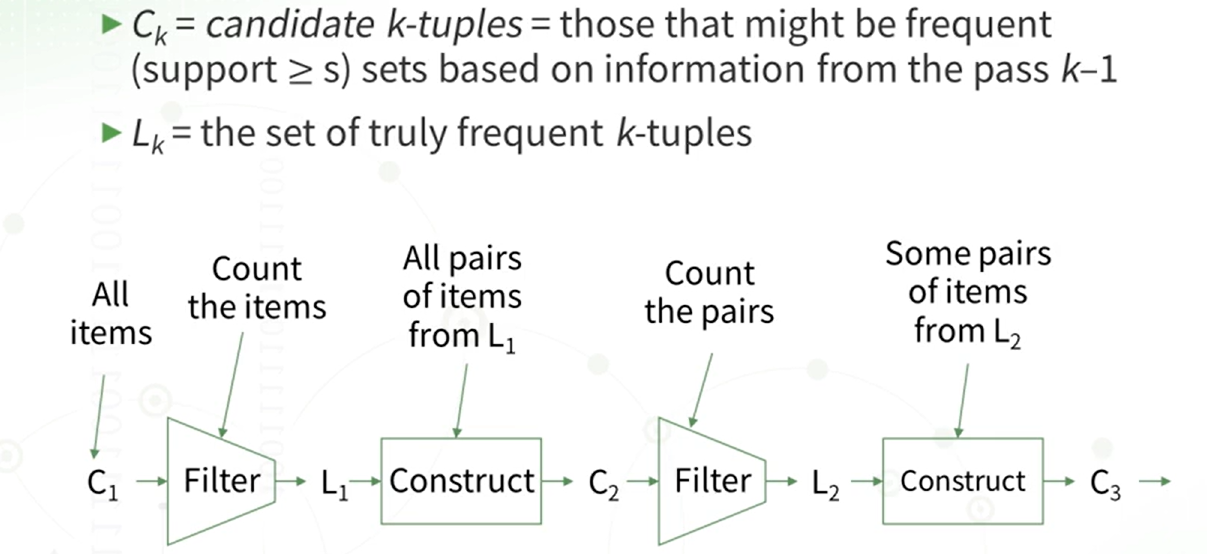
A-Priori 알고리즘은 Ck와 Lk를 반복하여 만드는 과정을 말합니다. 여기서 k가 2일 때 가장 많은 메모리가 필요하게 됩니다.

PCY(park-chen-yu) Algorithm

A-priori 유사하지만 다른 점

PCY(Principle of Counting with a Hash Table)는 A-Priori와 유사한 알고리즘이지만, 각각의 아이템 count를 세는 대신에 pair의 count를 세기 위한 해시 테이블을 유지합니다. 이 해시 테이블의 각 버킷은 해당 pair의 해시값을 가지고 있는 pair의 count를 포함하고 있습니다. A-Priori의 pass1에서 사용되지 않는 많은 메인 메모리 문제를 해결하기 위해, PCY에서는 각 pair를 해시하여 count가 s() 이상인지를 확인하는 것을 합니다.

pcy 알고리즘을 사용하였을 때 좋은점

PCY 알고리즘은 A-Priori와 다르게 개별적으로 빈발하는 아이템의 수가 많을 때에도 (2,3)과 (1,9)와 같은 쌍이 선발되지 않을 수 있습니다. PCY 알고리즘에서는 가장 작은 support 수를 지정하고, 쌍으로 묶은 후 해당 쌍의 Total count가 지정한 support 수를 넘지 못할 경우 탈락시킵니다. 즉, PCY 알고리즘은 A-Priori 알고리즘과 달리 개별 아이템의 쌍을 묶고, 최소 support에 미치지 못할 때 탈락한다는 점에서 다릅니다. 이는 PCY 알고리즘의 주된 아이디어라고 볼수 있습니다.

pass 1 메모리 사용량을 줄일수 있다.

• 각각의 버킷은 해당 쌍이 frequent 한지 여부만을 중요시합니다
• 버킷 값이 1이면 해당 버킷은 frequent한 것을 나타내며, 그 bit 값이 0이면 frequent하지 않음을 나타냅니다.

이러한 이유로 A-Priori 알고리즘에서는 버킷의 카운터를 약 32비트로 사용했지만, PCY 알고리즘에서는 1비트만으로도 frequent 여부를 구별할 수 있기 때문에 메모리 사용량을 크게 줄일 수 있습니다.

pass 2 쌍이 두가지 조건을 만족 해야된다.

• (i ,j ) 각각이 frequent 아이템 이어야 하고 ,
• 해당 쌍이 frequent한 버킷으로 해싱되어야 됩니다.

만약에 (i)와 (j)가 frequent하지만 (i,j) 쌍이 frequent 하지 않으면 셀 필요가 없게 됩니다.

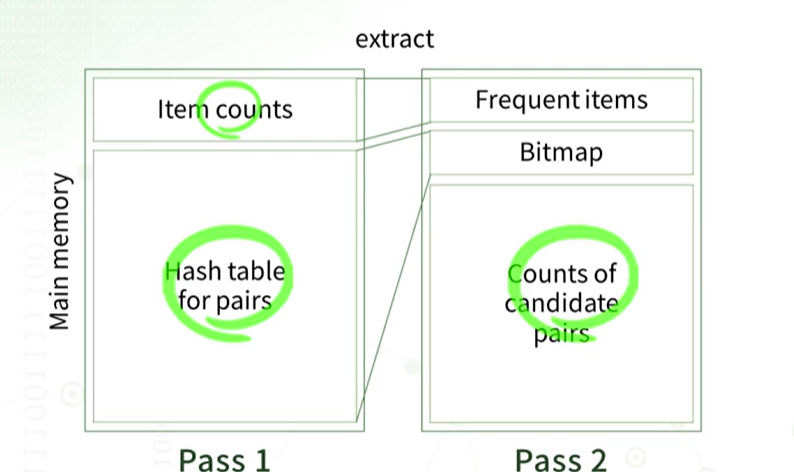
메인메모리 구조

중요한건 PCY 알고리즘을 활용한 변형 알고리즘

멀티 스테이지

변형 메모리

pass1에서는 pair의 수를 한 번 적어주고, pass2에서는 i와 j의 값이 모두 frequent한 조건을 만족할 때 실행됩니다. 그러나 이러한 조건을 만족하는 pair가 매우 적기 때문에, 각 버킷이 기여하는 pair의 수가 적어집니다. 결과적으로, 빈발하지 않지만 빈발한 것처럼 보이는 pair의 수를 줄일 수 있습니다.

PCY 알고리즘의 단점은 메모리가 한 번 더 사용된다는 것이지만, 까다로운 조건으로 인해 최종적으로 후보 pair의 수를 줄일 수 있어 더편리하고 효율적 입니다.
pass3에서는 3가지 조건을 모두 만족하면 count하게 됩니다.

멀티 해쉬

PCY에서 pass1 단계에서 여러 개의 해시 테이블을 동시에 사용하는 것은 원래 한 개의 해시 테이블만 사용하는 것과는 달리 메모리 사용량을 줄일 수 있는 잠재적인 장점이 있습니다. 그러나 이러한 접근 방식은 리스크도 동반합니다. 해시 테이블이 두 개인 경우, 각 테이블이 담을 수 있는 메모리 크기가 절반으로 줄어들게 됩니다. 그 count들이 minimum support 넘긴다면 , 의미 가없어 더 이상 효과적인 방법이 아니게 됩니다.

Random sampling

Market-Basket 데이터가 매우 큰 경우, 그 중 일부를 랜덤하게 샘플링하여 사용합니다. 예를 들어, 전체 바스켓의 10% 정보만을 랜덤하게 추출하는 것은 단 한 번의 데이터 읽기 과정만으로 이루어지므로 1-pass 알고리즘으로 간주됩니다.

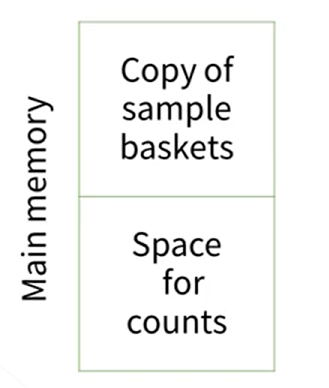
첫 번째로는 바스켓을 위한 샘플들이 포함되고, 두 번째로는 카운트를 위한 메모리가 할당됩니다. 그러나 바스켓 샘플이 매우 작기 때문에 모든 것이 메모리에 쉽게 저장될 수 있습니다. 여기서 주의해야 할 점은 원래의 minimum support가 있었지만 이제 샘플링을 하였으므로, 샘플 크기에 맞게 minimum support를 조정해야 한다는 것입니다. 예를 들어, 전체 데이터에서는 20번 이상 나타나야 하는데, 1/4의 데이터만 사용한다면 5번 이상 나타나면 충분합니다.

그러나 이러한 Random sampling은 전체 데이터가 아닌 일부 데이터만 샘플링되었기 때문에 오류가 발생할 가능성이 있습니다. 이는 주요한 리스크 요인 중 하나입니다.

Random sampling 의 단점 일부 데이터만 샘플링 했기 때문에 오류가 생기게 됩니다.

False positive

실제로는 빈발하지 않지만 빈발한 것처럼 나타나는 아이템을 발견한 후, 실제로 빈발한지를 확인하기 위해 한 번 더 패스를 실행하여 검증할 수 있습니다. 이를 통해 해당 아이템이 실제로 빈발한지 여부를 확인하고, 필요하다면 제거할 수 있습니다.

False negative

실제로는 빈발한 아이템셋이지만 알고리즘 실행 결과에는 빈발하지 않은 것으로 나타나는 경우가 있습니다. 이는 False positive라고 합니다. False positive의 경우에는 오류를 제거할 수 없는데, 그 이유는 원래 아이템셋이 존재했지만 우연히 랜덤하게 샘플링된 아이템셋이 해당 빈발성을 충분히 포착하지 못할 수 있기 때문입니다.

False negative를 줄이기 위한 한 가지 좋은 방법은 minimum support를 줄이는 것입니다. Minimum support를 줄이면 조금만 나타나도 아이템셋이 빈발한 것처럼 보이기 때문에 오류를 줄일 수 있습니다. 그러나 이렇게 minimum support를 줄이면 frequent한 후보 아이템셋이 많아지므로 메모리 요구량이 늘어날 수 있습니다. 또한, 실제로는 빈발하지 않은데 빈발한 것으로 나타나는 False positive가 증가할 수 있습니다. 이러한 장단점을 고려하여 적절한 선택이 필요합니다.

SON 알고리즘

현재 전체 데이터가 매우 크기 때문에 문제가 발생합니다. 이를 해결하기 위해 전체 데이터를 k개의 chunk로 나누는 방법을 사용할 수 있습니다. 예를 들어, k가 10이라면 전체 데이터를 10개의 조각으로 나눈 후 각각의 조각을 메인 메모리로 읽습니다. 각각의 조각은 메모리에 쉽게 들어갈 정도로 작다고 가정합니다. 그런 다음 메모리에 올려진 각각의 조각에서 알고리즘을 실행하여 모든 frequent itemset을 찾습니다.

원래의 minimum support가 s였다면 이를 k개의 chunk로 나눈 경우에는 minimum support를 k분의 s로 줄여주어야 합니다. 각각의 chunk에서 candidate를 찾은 다음에 한 번 더 pass를 돌려서 전체 바스켓에서 실제로 frequent한 candidate를 확인합니다. 이때, 모든 chunk에서 빈발하지 않았다면 전체적으로 support가 s보다 작아지게 됩니다. 각각의 chunk에서 candidate를 찾은 다음에 한 번 더 pass를 돌려서 전체 바스켓에서 실제로 frequent한 itemset을 찾는 것입니다. 따라서 앞에서 설명한 monotonicity 개념이 여기서 나오게 됩니다. 목표는 전체 n개의 바스켓에서 최소 s번 이상 나온 itemset을 찾는 것인데, 이 n개의 바스켓을 k개의 chunk로 나누었기 때문에 이를 고려하여 minimum support를 조정하고, 각각의 chunk에서 frequent한 candidate를 찾은 다음 전체 바스켓에서 실제로 frequent한 itemset을 찾아내는 것입니다.

이글을 마치며

지금까지 Market Basket Analysis에 대한 알고리즘 및 메모리 구성에 대해 살펴보았습니다.