Projection
1. Perspective
-> 원근 투영
-> z값에 상관없이 투영을 Clip space를 직육면체로 가져오기 때문에 z값에 대한 크기 변화가 있음
2. Orthographic
-> 직교 투영
-> z값에 상관없이 투영을 Clip space를 직육면체로 가져오기 때문에 z값에 대한 크기 변화가 없음
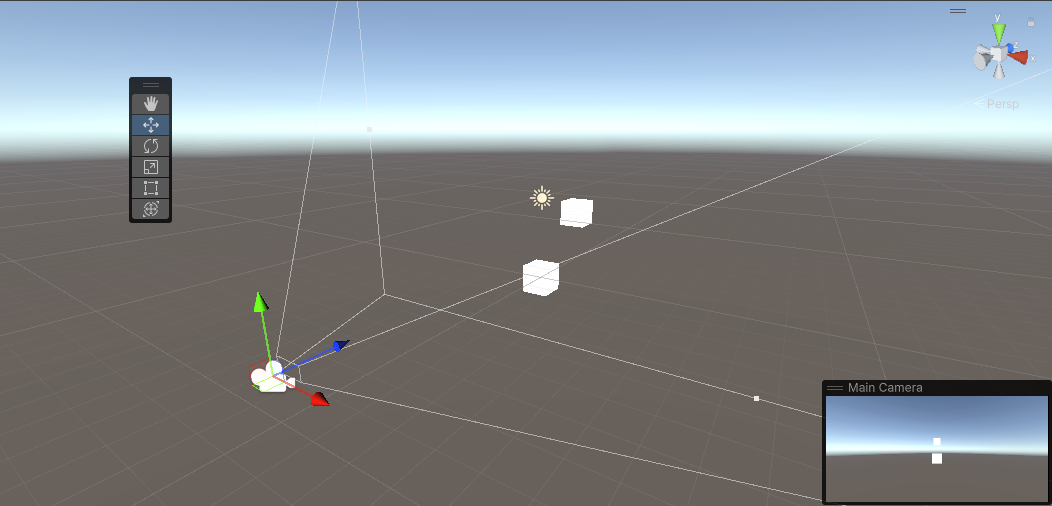
Perspective Projection
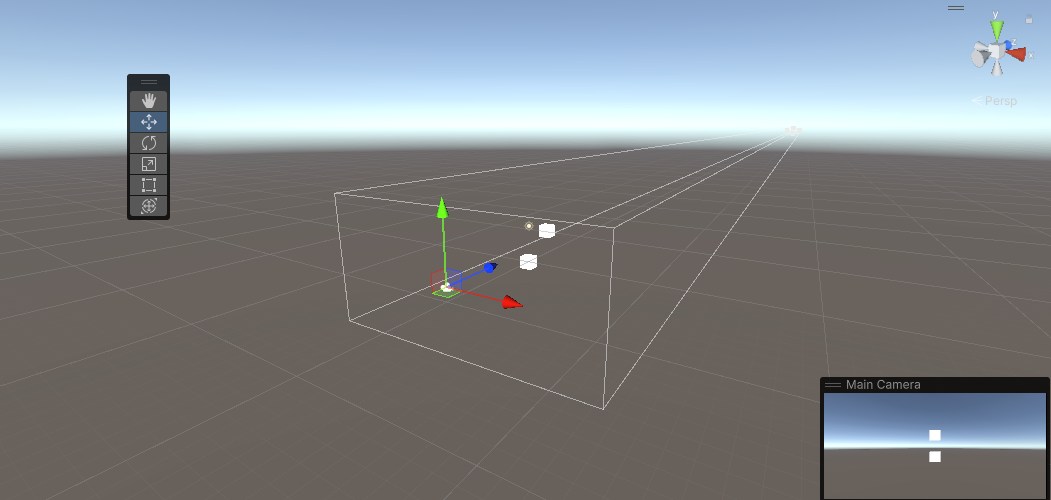
Orthographic Projection
[출처 : Unity My Proejct]
Perspective Projection
Orthographic Projection
[출처 : Direct X My Project]
View Space
Camera space 또는 View Space라고도 하며, World Space에 있는 오브젝트를 결국 2D 스크린에 투영하기 위해서는 View Space 즉, Camera View안에 들어야와야한다.
카메라 공간 유의 사항
1. 카메라는 항상 원점이 되어야할 것
2. 앞은 항상 Z축일것
이를 유의하며, 예시를 들며 View Space를 이해해나갈 것이다.
이해를 위해서 카메라라는 오브젝트가 있다고 하자, 해당 오브젝트를 World Space로 옮긴다고 가정하면, Scale 값은 중요치 않으니, 제외하고 W = RT라는 행렬을 곱해줄것이다. 이 때 ViewSpace는 곧 RT라는 행렬이 곱해진 좌표가 원점이 되는 Space 즉, 다른 물체는 WorldSpace에서 해당 원점과 반대되게 움직이게 될것이다.
즉, 다른 물체에 View Space에 대한 좌표를 구하려면 W^-1 = (RT)^-1을 곱해줘야 할것이다.
즉, T^-1 * R^-1 이 될것이고, T ^ -1 같은 경우는 말 그대로 Camera Object에 반대로 움직일 것이고
카메라 좌표(0,0,0)
카메라 좌표(1,0,0)
R은 즉, T정보가 빠진, 해당 카메라 오브젝트의 x,y,z 축의 정보
x축 (Ux,Uy,Uz,0) y축 (Vx,Vy,Vz,0) Z축(Wx,Wy,Wz,0) 이다.
| Ux,Uy,Uz,0 |
| Vx,Vy,Vz,0 |
| Wx,Wy,Wz,0 |
| 0 0 0 1 |
해당 행렬의 역행렬를 구해주면 된다.
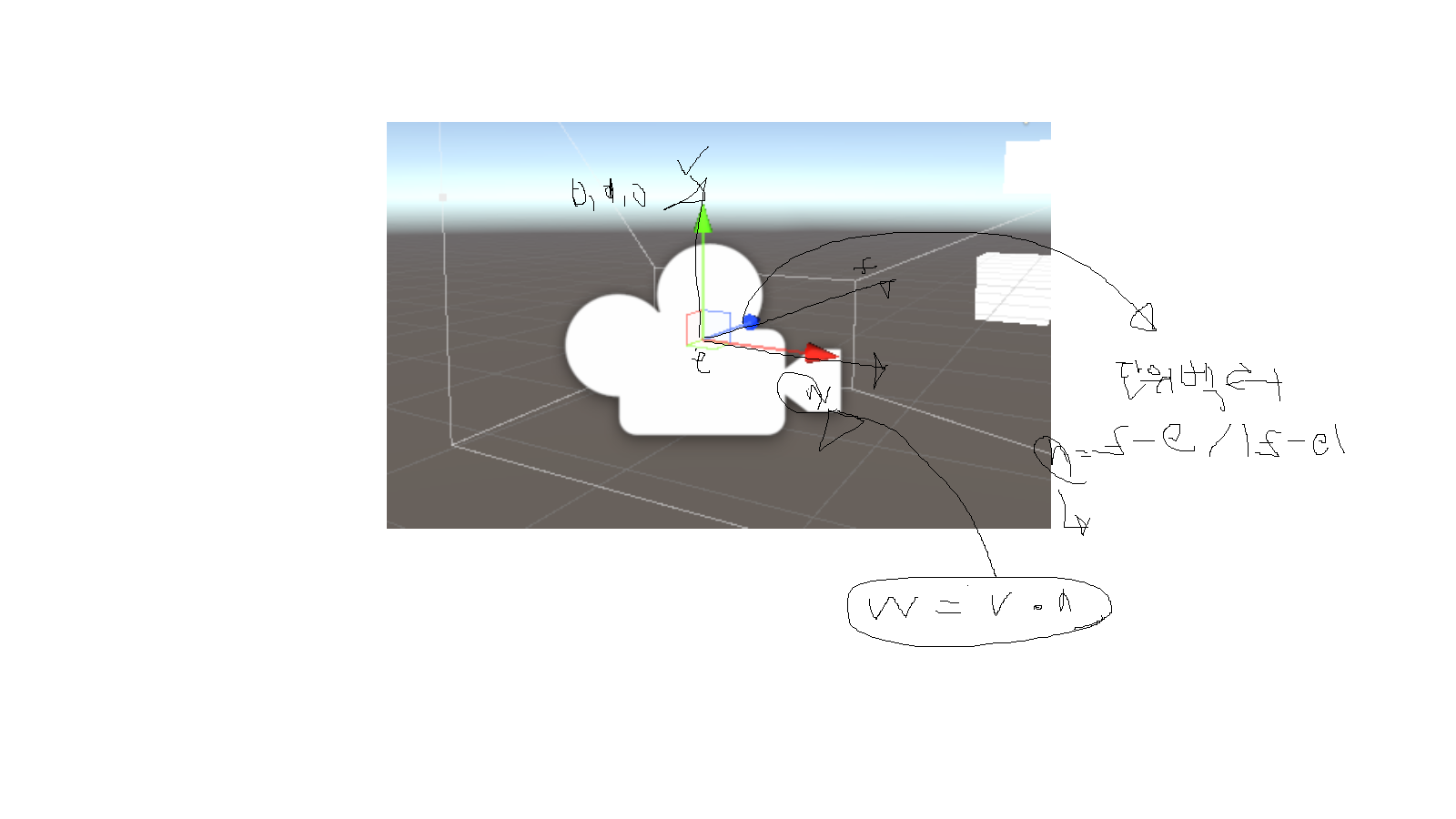
그림이 허접하지만 해당 식으로 해결을 해줘야하지만, 간단하게 Object의 X,Y,Z축을 Transform 구조체에 저장시켜놓고 사용하기로 했다.
월드 행렬을 구하면서 R 값이 해당 오브젝트 X,Y,Z축에 갱신이 되게 하였다.
이 행렬의 역행렬을 구해주면되는데 해당 행렬은 직교행렬로 역행렬이 그저 전치만 해주면 된다.