62. Unique Paths

문제 설명

링크
)

접근 1 - bfs

• 오른쪽 또는 아래로 이동 가능한 좌표들로 queue 에 넣어서 finish 지점에 도착하면 경우 ++
• 시간초과

코드 1

    def uniquePaths(self, m: int, n: int) -> int:
        start = [0, 0]; end = [m - 1, n - 1]
        ans = 0
        dq = collections.deque([start])
        directions = [[0, 1], [1, 0]]
        while dq:
            i, j = dq.popleft()
            if [i, j] == end:
                ans += 1
                continue
            for d in directions:
                x, y = i + d[0], j + d[1]
                if x < m and y < n:
                    dq.append([x, y])
                    
        return ans

접근 2 - 경우의 수

• 최단거리 경우의 수 문제와 같게 접근
• board[i][j] = board[i-1][j] + board[i][j-1]

코드 2

    def uniquePaths(self, m: int, n: int) -> int:
        board = [[0] * n for _ in range(m)]
        board[0][0] = 1
        for i in range(m):
            for j in range(n):
                if i >= 1: board[i][j] += board[i - 1][j]
                if j >= 1: board[i][j] += board[i][j - 1]
                    
        return board[m-1][n-1]
        
        
 --- O(n) space ----
        dp = [1] * n
        for i in range(1, m):
            for j in range(1, n):
                dp[j] += dp[j-1]
        return dp[n-1]

64. Minimum Path Sum

문제 설명

링크

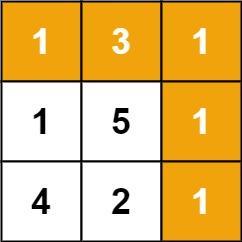
Input: grid = [[1,3,1],[1,5,1],[4,2,1]]
Output: 7

접근

• 위의 방법과 비슷
• board 의 값을 갱신할 때, 최소값을 넣도록 함

코드 1

    def minPathSum(self, grid: List[List[int]]) -> int:
        m = len(grid); n = len(grid[0])
        for i in range(m):
            for j in range(n):
                if i >= 1 and j >= 1: grid[i][j] += min(grid[i - 1][j], grid[i][j - 1])
                elif i >= 1: grid[i][j] += grid[i - 1][j]
                elif j >= 1: grid[i][j] += grid[i][j - 1]
        return grid[-1][-1]