[Python] 백준 28217) 두 정삼각형

🔗문제 링크

28217번: 두 정삼각형

✅ 문제 유형

구현, 시뮬레이션

🤔 문제 풀이

구현 문제로 특정한 알고리즘은 쓰이지 않습니다. 다만 구현을 위한 특별한 아이디어는 필요합니다 ! 처음 문제를 보고 삼각형 회전을 3번 시키면 원형으로 돌아오기 때문에 수학적인 규칙이 있지는 않을까? 생각하고 규칙을 기반으로 알고리즘을 생각했으나 딱히 규칙을 발견하지 못 했습니다.

그래서 ‘회전’의 의미에 대해서 집중해 보았는데요. 밑에 그림은 시계 방향으로 한바퀴 회전했을 때의 정삼각형이 어떤 인덱스(편의상 인덱스의 시작은 1)를 가지는지 나타내 보았습니다.

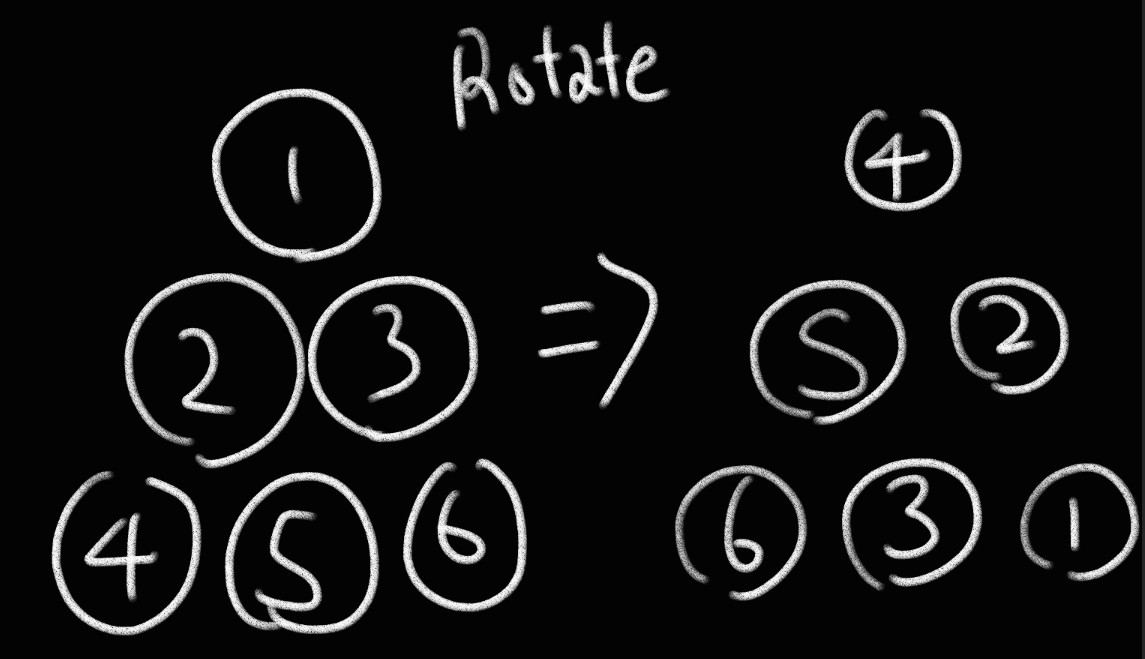
정삼각형의 밑변은 6,3,1 이 됩니다 ! 한번 더 회전하면 밑변이 어떻게 구성될까요? 1,2,4입니다. 이 부분을 조금 더 생각해보면 다음 그림과 같이 회전에 대해서 정의할 수 있습니다. 3줄 친 부분이 곧 밑변이 되는 인덱스들을 나타낸 것입니다.

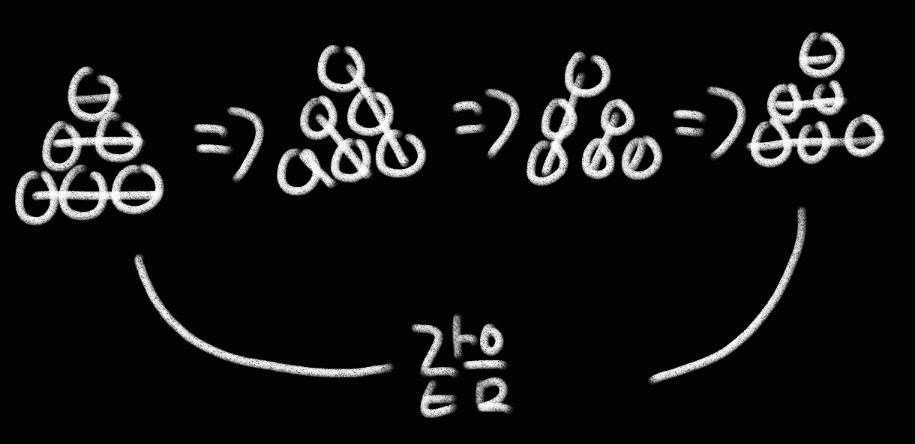
회전과 인덱스들의 관계에 대해서 이해했으니 이걸 파이썬 코드로 이중 반복문을 통해 구현하면 문제는 90% 끝입니다 ! 회전 코드는 rotate 함수로 정의하였습니다.

📖 코드

import sys
input = sys.stdin.readline

# 문제 입력
N = int(input())


A=[]
B=[]

for i in range(N):
    A.append(list(map(int,input().split())))

for i in range(N):
    B.append(list(map(int,input().split())))


# 회전의 경우 반시계나 시계나 돌리나 사실 같은 경우의 수가 나옴.
# 하나의 회전 방향만을 고려한다.

# 반시계로 회전 구현.
def rotate(A):
    tmp = []
    for i in range(1,N+1):
        tmp.append([i for i in range(i)])

    for i in range(N): # 아래 선분의 기준, 인덱스의 기준
        for j in range(i,N): # 선분의 요소 대입
            tmp[N-i-1][j-i] = A[j][i]

    return tmp

# 현재 정삼각형과 B의 차이가 얼마인지 구하는 함수.
def calculator(A,B):
    cnt = 0

    for i in range(N):
        for j in range(i,N):
            if A[j][i] != B[j][i] :
                cnt+=1

    return cnt

MIN = 1e9 # 매우 큰 값 설정

# 대칭하지 않은 삼각형과 B의 차 구하기.
for i in range(3):
    MIN = min(MIN,calculator(A,B))
    A = rotate(A)

# 대칭한 삼각형 값 구하기.

symmetry = [] # 대칭한 삼각형
for i in range(1,N+1):
    symmetry.append([i for i in range(i)])

# 대칭 구현
for i in range(N):
    for j in range(i+1):
        symmetry[i][i-j] = A[i][j]

# 대칭한 삼각형과 B의 차 구하기
for i in range(3):
    MIN = min(MIN,calculator(symmetry,B))
    symmetry = rotate(symmetry)

print(MIN)