[JS Algorithm] 자바스크립트 Sorting - 심화편 #01 Merge sort

Young-mason·2021년 2월 19일

Algorithm

목록 보기

3/4

💡 자바스크립트 언어로 자료구조 & 알고리즘에 대해 배운 내용을 기록합니다

📖 Intro

이전에 알아보았던 bubble, insertion, selection 정렬은 전반적으로 O(n^2) 의 시간복잡도를 가지므로, 배열의 길이가 커졌을때 상당히 비효율적인 알고리즘이 됩니다.

이러한 시간복잡도를 O(n logn)으로 개선할 수 있는 정렬 알고리즘들이 있습니다. 대표적인 것들이 Merge, Quick, Radix Sort인데요, 이 알고리즘들은 보다 더 효율적이지만, 그만큼 구현하기에 더 복잡하다는 점이 있습니다.

이번 포스트에서는 병합 정렬 (Merge Sort)의 작동 방식을 알아보면서 자바스크립트 코드로 구현해보겠습니다.

📖 병합 정렬 (Merge Sort)

병합정렬은 병합(merging)과 정렬(sorting) 두가지 큰 기능으로 구성됩니다. 길이가 0이나 1인 배열은 항상 정렬되어 있는 상태라는 점을 활용해서, 배열을 0개 혹은 1개의 요소로 모두 분리시킨 뒤, 배열을 새롭게 재구성(병합) 하면서 정렬시키는 정렬 방식입니다.

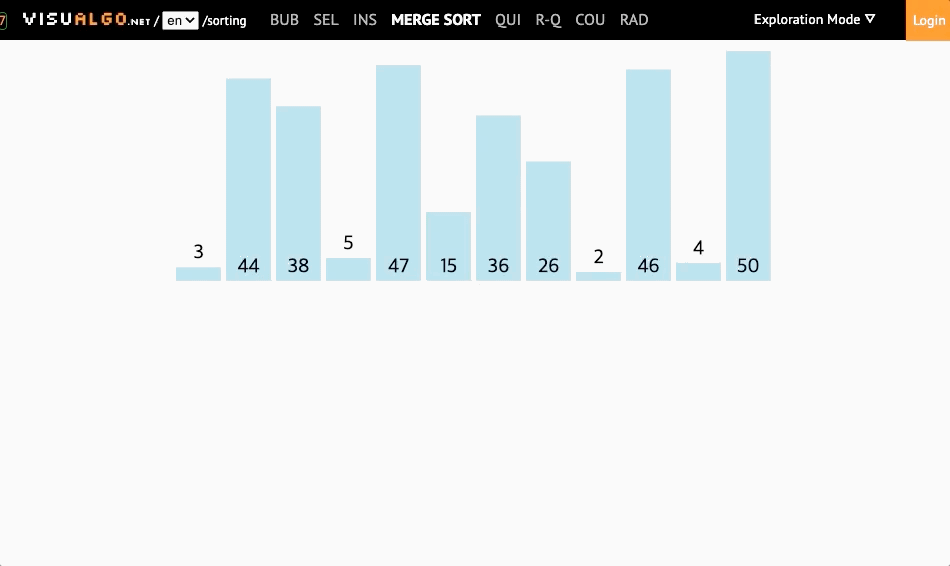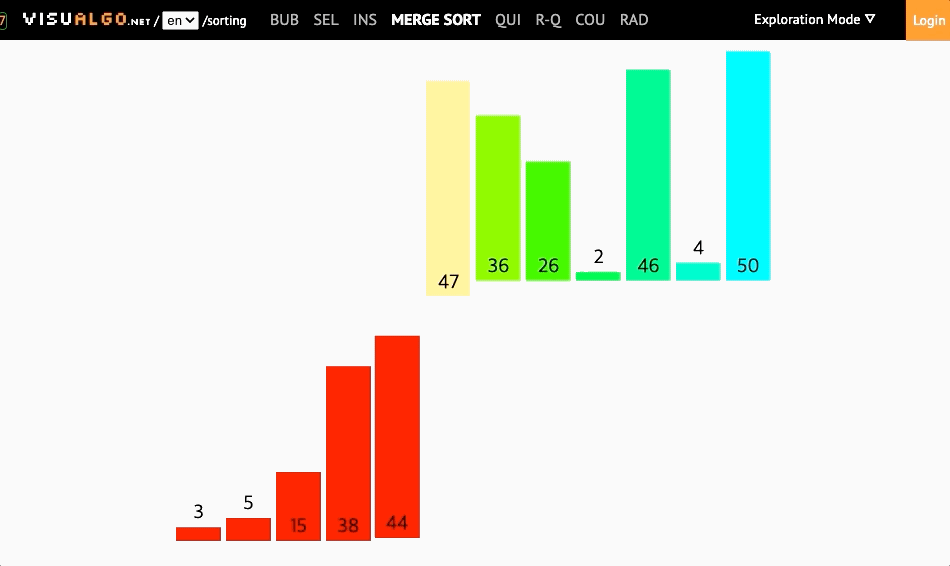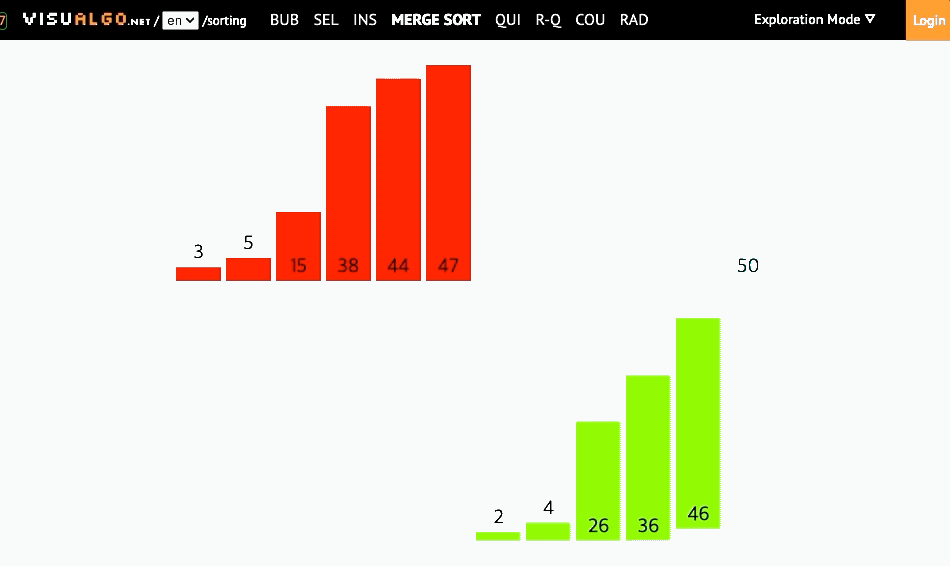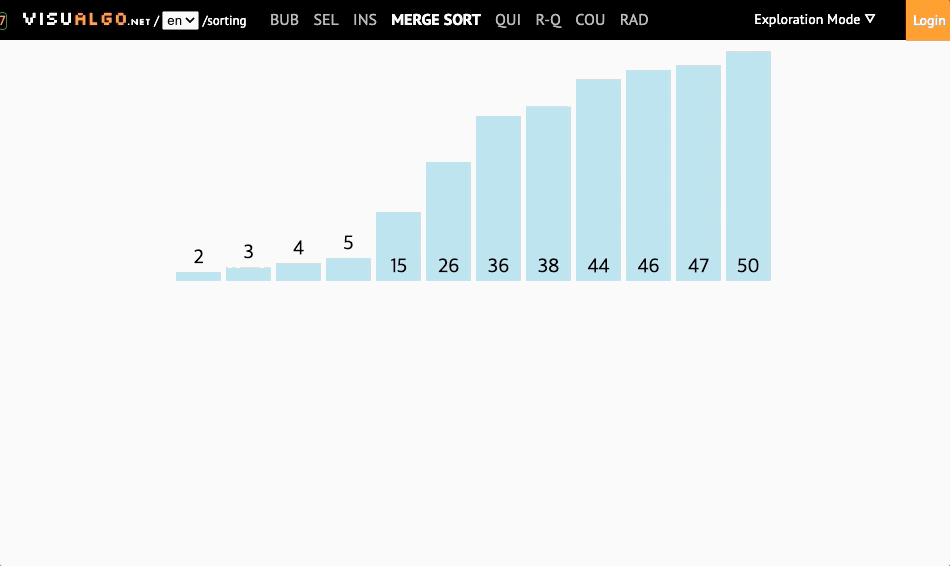
1. merge 함수 만들기

병합 정렬을 구현하기 위해서, 먼저 두개의 정렬된 배열을 하나로 병합하는 함수를 구현해보겠습니다.

병합되는 배열은 정렬 되어 있어야하며, 두 Input 배열의 모든 요소가 들어있어야 합니다. 또한, Input 배열들이 수정되면 안됩니다.

두 배열의 모든 요소를 순회하게 되므로 O(n+m) 의 시간복잡도와 공간복잡도로 동작하게 됩니다.

[Pseudocode]

빈 배열을 만들고, 각 input 배열의 0번째 인덱스를 포인터(i, j) 변수에 저장해둔다
반복문을 통해 두 배열을 동시에 탐색한다
- 만약 첫번째 배열의 값이 두번째 배열의 값보다 작다면, 첫번째 배열의 값을 result 배열에 담고 첫번째 배열의 포인터를 증가시킨다
- 만약 첫번째 배열의 값이 두번째 배열의 값보다 크다면, 두번째 배열의 값을 result 배열에 담고 두번째 배열의 포인터를 증가시킨다
- 만약 한 배열의 순회가 끝나면, 나머지 배열의 남은 요소들을 차례대로 result 배열에 담는다

function merge(arr1, arr2) {
  let result = [];
  let i = 0;
  let j = 0;
  
  while ( i < arr1.length && j <arr2.length) {
    if (arr2[j] > arr1[i]) {
      result.push(arr1[i]);
      i++;
    }
    else {
      result.push(arr2[j]);
      j++;
  }
    
  while ( i < arr1.length) {
    result.push(arr[i]);
    i++;
  }  
    
  while ( j < arr2.length) {
    result.push(arr[j]);
    j++;
  }
    
  return result;  
}

2. Merge sort 구현하기

이제 위에서 만든 merge 함수를 활용하여, Merge sort의 전체 로직을 구성해보겠습니다.

[Pseudocode]

빈 배열 혹은 1개 요소만 남을 때 까지 배열을 반으로 쪼갠다
정렬된 상태의 쪼개진 배열을 위에서 구현한 merge 함수를 실행하면서 원래의 배열 길이가 될 때까지 병합시킨다
병합 & 정렬된 배열을 리턴한다

function mergeSort(arr) {
  let (arr.length <= 1) return arr;
  
  let mid = Math.floor(arr.length / 2)
  let left = mergeSort(arr.slice(0, mid));
  let right = mergeSort(arr.slice(mid));
  
  return merge(left, right);
}