🌈 시작하며
최근에 코테 스터디에서 해당 문제를 냈어요.
풀이 방법은 행렬의 원리만 알고 있다면, 매우 간단한 문제였어요.
하지만 어떻게 해당 점화식을 반복문으로 전개해나가야 할지에 대해 거의 하루를 들여 상당히 많은 고민을 했어요. 그리고 그 과정에서 많은 것을 배웠답니다.
이 글은, 복기와 동시에 어떻게 해당
DP점화식을 반복문으로 구현하지?라고 생각하신 분들에게 영감을 주기 위한 글이에요! 도움이 되길 바라며 🙇🏻♂️
🔍 본론
저는 알고리즘 문제를 풀 때 항상 문제를 잘게 쪼개는 습관을 갖고 있어요.
따라서 먼저 다음과 같은 순서로 문제를 풀었답니다.
풀이 과정
- 결국 이전의 값을 참조하여 최소값을 구하는 로직을 보며, 일정한 점화 식을 갖고 푸는 듯한 느낌이 보였어요.
- 따라서 이를 DP로 풀어야겠다고 생각했습니다! 따라서 어떤 주어진 해를 찾기 위한 점화식을 찾아야했어요.
- 점화식을 찾는다면, 이를 DP로 구현하기 위한 배열을 생성해야겠다고 생각했습니다.
- 점화식에 맞춰 배열에 적용해야겠어요!
- 결과 값을 반환합니다.
대충 이런 플로우를 예상하고, 문제에 접근하기 시작했어요.
점화식을 찾자
우리에게 ABCD라는 행렬이 주어졌다고 생각해보아요.
행렬의 곱 연산 수는 결국 X, Y를 곱하였을 때 다음과 같은 값이 나온답니다.
XY=X의 행 * Y의 행 * Y의 열
이때 특이한 것은, 어떤 것을 먼저 곱하든지 간에 연산은 완료될 수 있다!는 점이에요.
즉, ABCD = AB * CD가 될 수 있고, ABC * D가 될 수도 있어요. 또한, A * BCD가 될 수도 있죠!
이때 뭔가 특이한 것이 보이기 시작해요.
결국 ABC, BCD도 어떤 특정한 연산을 통해서 나올 건데...?
ABC = Math.min(AB * C, A * BC)
BCD = Math.min(BC * D, B * CD)
ABCD = Math.min(A * BCD, AB * CD, ABC * D)
- 아! 결국 이전의 연산의 값이 현재의 값에 영향을 미치는 구나!
- 그리고 저
*연산자를 하나의 구분자로 본다면, 결국 행렬 n개를 곱한 연산의 최소값은 n-1개의 연산 중 최소값을 찾는 것이겠구나!
따라서 DP에서 캐싱해줘야 할 값은 이전에 계산한 행렬의 곱 연산 최소 값이었어요.
따라서 저는 DP를 위한 배열의 인덱스 값을 다음과 같이 정의했어요.
DP(i,j) =
i번째 행렬에서j번째 행렬까지의 연산 최소 값
그리고 이를 구분자가 있는 인덱스 값을 k라는 변수로 선언한다면, 다음과 같은 점화식이 완성이 되겠죠? 😉
DP[i][j] = DP[i][k] + DP[k + 1][j] + (i번째 행렬의 행 * j번째 행렬의 행 * j번째 행렬의 열)
자, 점화식을 구했으면 우리는 이제 실전으로 구현에 들어가 보죠! 🙆🏻
반복문으로 이제 구현하자!
저는 반복문 쪽이 많이 어려웠어요.
일단 어떻게 구현해야겠다는 설계는 어렵지 않았답니다.
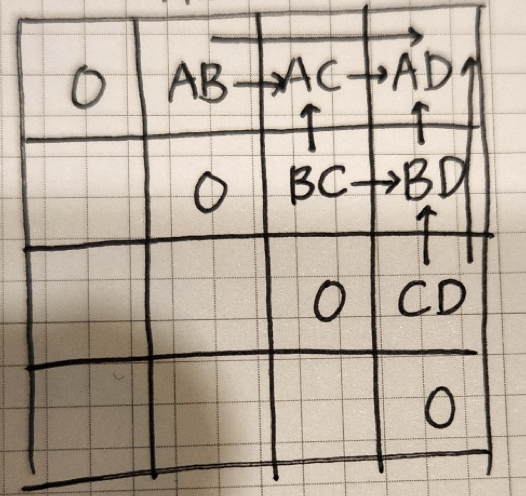
문제를 풀면서 일종의 표를 그려봤는데요.
결국, 어떤 i ~ j 번째 행렬로 가기 위해서는,
- 왼쪽의 배열값들과
- 아래쪽의 배열값들
이 두가지를 알아야 해요.
왜냐! 결국 현재의 인덱스 값은 같은 행의 이전 열의 값과, 다음 행의 같은 열 값에 영향을 받고 있기 때문이죠!
따라서 우리는 오른쪽 아래 대각선 방향으로 미리 선행 값들을 구해야 한다는 것을 유추할 수 있어야 해요.
하지만 제게 시련이 닥쳤는데요.
... 이걸 어떻게 구하죠...? 😢
대착각 - 무조건 인덱스를 기반으로 행,열 값을 매겨야 한다.
여기서 저는 엄청난 편견으로 인해 약 하루를 헤매게 됩니다. (...)
바로 행, 열 값을 매기는 기준을 무조건 인덱스로 치환하는 버릇이었는데요.
이 말이 이해가 안 될 수도 있지만, 저는 이런 습관을 갖고 있었어요.
for (let row; row < len; row += 1) {
for (let col; col < len; col += 1) {
...
}
}즉 반복문에서 선언한 인덱스에 한정하여 배열의 인덱스 값에 접근하는 방식에 갇혔기에, 대각선의 경우는 발상을 떠올리기 힘들었어요. 🥲
아이디어 - 행렬의 값을 인덱스에 한정짓지 말고, 분리하자.
결국 오른쪽으로 대각선을 간다는 것은, 행의 값이 고정되어 있지 않아야 한다는 대전제가 존재합니다!
따라서 이를 분리하여 실행하니, 뭔가 감이 잡혔어요.
for (let i = 1; i < len; i += 1) {
for (let row = 0; row + i < len; row += 1) {
const col = row + i;
for (let k = row; k < col; k += 1) {
...
}
}
}즉, 위와 같은 반복문을 고려하게 된 거죠!
쉽게 설명하자면... i번 도는 로직을 위에 놓아준다면, row는 이제 기준 인덱스인 k가 끝날 때마다 i만큼씩 값을 증가시킬 수 있어요. 단, row + i가 전체 길이보다 커지지 않는다는 조건은 있어야겠죠? 😉
이때, col 역시 동적으로 값이 변경이 되고, 따라서 오른쪽 아래로 이동하면서, 기준점 역시 행렬의 크기 사이에서 조정이 가능하게 되었어요!
자. 그렇다면 기존 점화식을 배열에 맞춰서, 적용해봐야겠죠?
for (let i = 0; i < matrixLength; i += 1) {
dp[i][i] = 0;
}
for (let i = 1; i < matrixLength; i += 1) {
for (let row = 0; row + i < matrixLength; row += 1) {
const col = row + i;
for (let k = row; k < col; k += 1) {
dp[row][col] = Math.min(
dp[row][col],
dp[row][k] +
dp[k + 1][col] +
matrix_sizes[row][0] * matrix_sizes[k + 1][0] * matrix_sizes[col][1]
);
}
}✨ 마치며
발상은 참 쉬웠는데, 구현 과정에 있어서 너무나 유연성이 부족했기에, 이러한 실수가 발생했어요.
하지만 덕분에, 앞으로는 어떻게 매트릭스에 관한 문제에 접근해야 할지, 감을 잡을 수 있어 행복했답니다.
결국 알고리즘 공부의 핵심은, 많이 푸는 것에 있으면서도 내가 이를 구현하는 데 있어 유연성을 갖고 바라볼 수 있는지인 것 같아요. 덕분에 생각을 정말 많이 하게 됐네요! 🥰
이 글을 보는 분들 모두, 즐거운 프로그래밍 하시길 바라며. 그럼, 이상! 👋🏻
.jpg)