🌈 시작하며
다시 또 여행을 다녀온 뒤로, 마음을 다잡기 위해 자고 일어나서 바로 코딩을 합니다 😉
최근에 배열 관련 문제를 많이 냈는데, 이번에도 괜찮은 문제를 하나 들고 왔어요.
바로 이 문제인데, 난이도는 낮지만 아이디어를 배열로 풀지 못하면 꽤나 고전할 문제입니다.
분명 이 문제를 풀면서 자괴감을 가질 수도 있으나, 생각만 다르게 하면 어려운 문제가 아니에요. 같이 풀어나가보죠! 🙆🏻
✅ 풀이과정
자료구조 선택 - 배열
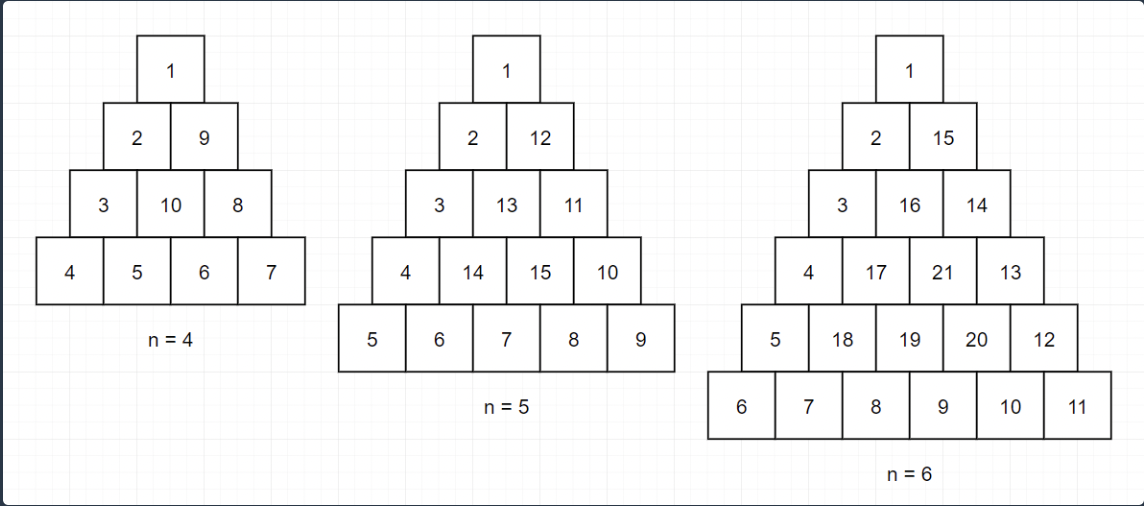
일단 이 문제를 살펴봅시다. 이 문제는 정삼각형처럼 그림이 제시되어 있어요.
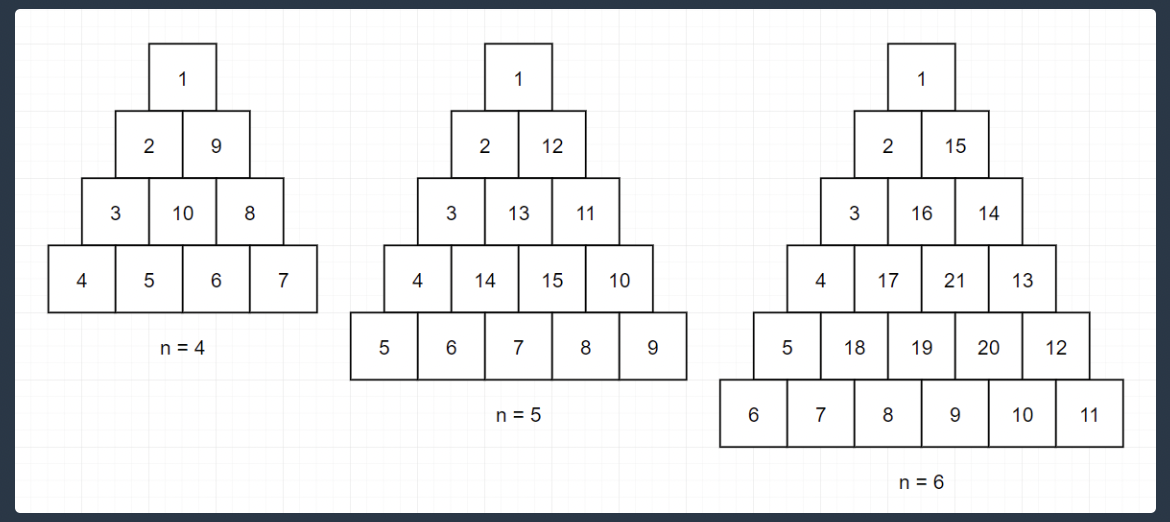
처음에 당황스러울 수 있어요. 어떻게 이를 저장해야 할지 말이죠.
그런데, 잘 생각해보면, 이는 출제자가 이 문제를 쉽게 정의하지 못하도록 한 트릭입니다.
결국, 이를 배열로 저장을 할 때, 가로와 세로 변의 길이가 같은 이등변 삼각형으로 보면 어떨까요?
위의 전제로 계산하여 문제를 풀어나가도, 큰 이상이 없다는 것을 파악하실 수 있어요.
따라서 우리는 다음 한 가지를 얻을 수 있습니다.
- 문제의 해는 배열에 값을 저장함으로써 풀어나갈 수 있다.
따라서 배열을 생성해봅시다!
const solution = (n) => {
const answer = [];
const arr = Array.from({ length: n }, () => new Array(n).fill(0));
...
}문제 해결 방법 설계 - 알고리즘
자, 우리는 이제 패턴을 해석하고, 이 문제를 해결할 수 있는 알고리즘을 도출해야겠죠?
처음에 머리가 어지러울 수 있어요.
우리가 흔히 하는 for 문으로 행 -> 열 순으로 접근하여 값을 할당하는 로직으로는 문제를 해결할 수 없다는 것을 알아버렸기 때문입니다.
아마 이 글을 찾으시는 분들도, 이러한 배열 접근법이 낯설어서 오신 거라 생각해요.
1. 행, 열 값을 동적으로 접근하자!
그런데, 배열에 값을 할당하는 문제들에는 대개 크게 2가지로 접근할 수 있어요.
for문의 초기 선언된 값에 전적으로 의존하여 행 -> 열로 접근하는 방법- 초기 선언된 값의 변화에 따라 동적으로 행, 열 값을 접근하는 방법
이 문제는 1번이 아닌 2번으로 풀어야 합니다.
이를 위해 다음과 같이, 행과 열 값을 반복문 외부에서 컨트롤 해주기로 했어요.
const solution = (n) => {
...
let row = -1; // 시작값은 항상 행 값이 +1되므로 -1부터 시작.
let col = 0;
for (let i = n; i > 0; i -= 1) {
...
}
...
};2. 삼각형의 값의 변화를 패턴화하자!
이게 가장 중요한데요. 우리, 삼각형을 따라가보죠.
n = 4이라고 할 때, 행과 열을 접근하는 인덱스 값의 변화를 관찰해볼까요?
[0, 0] - [1, 0] - [2, 0] - [3, 0] - [3, 1] - [3, 2] - [3, 3] - [2, 2] - [1, 1] - [2, 1]
뭔가 3종류의 값 변화 패턴으로 이를 나눌 수 있겠다는 생각이 직감으로 드시나요?
바로 다음과 같이 말이죠!
- 행의 값만 증가:
[0, 0]-[1, 0]-[2, 0]-[3, 0](4개) - 열의 값만 증가:
[3, 1]-[3, 2]-[3, 3](3개) - 행, 열 값 감소:
[2, 2]-[1, 1](2개) - 다시 행의 값 증가:
[2, 1](1개)
또한 특이한 점이 있어요.
하나의 방향이 바뀔 때마다, 이번에는 패턴에 맞게 변화하는 개수가 하나씩 감소하는 게 확인 가능하죠!
따라서 우리는 2개의 패턴을 확인했습니다.
- 2. 문제의 해를 풀어나갈 때에는 3개의 방향을 동적으로 변화시켜야 한다.
- 3. 방향이 변화할 때마다, 변화시켜야 할 값 개수는 n부터 시작하여 하나씩 감소한다.
그럼 따라서 이에 맞게 방향을 만들어주고, 값을 동적으로 변화시켜볼까요?
...
const directions = [
[1, 0],
[0, 1],
[-1, -1],
];
let row = -1;
let col = 0;
let nowValue = 1;
let nowDirectionIndex = 0;
for (let i = n; i > 0; i -= 1) {
const [dRow, dCol] = directions[nowDirectionIndex];
for (let j = 0; j < i; j += 1) {
row += dRow;
col += dCol;
arr[row][col] = nowValue;
nowValue += 1;
}
nowDirectionIndex = (nowDirectionIndex + 1) % 3;
}
...자, 그러면 우리는 이제 결과 값을 2차원 배열로 저장했는데요. 이제 결과 값에 맞게 변환시켜줘야 하겠습니다!
결과 값 반환
2차원 배열 -> 1차원 배열로 변환할 때, 우리는 모든 배열의 값을 접근한 게 아니라, 삼각형의 값만 바꾸었잖아요?
그렇기 때문에 삼각형의 값만 따로 빼야 해요.
여기서 아이디어는, 초기 값인 0은 현재 주어진 문제에서 나올 수 없으니, 0이 아닌 것들만 순서대로 푸시해주죠!
for (let i = 0; i < n; i += 1) {
for (let j = 0; j < n; j += 1) {
if (arr[i][j]) answer.push(arr[i][j]);
}
}전체 코드
const solution = (n) => {
const answer = [];
const arr = Array.from({ length: n }, () => new Array(n).fill(0));
const directions = [
[1, 0],
[0, 1],
[-1, -1],
];
let row = -1;
let col = 0;
let nowValue = 1;
let nowDirectionIndex = 0;
for (let i = n; i > 0; i -= 1) {
const [dRow, dCol] = directions[nowDirectionIndex];
for (let j = 0; j < i; j += 1) {
row += dRow;
col += dCol;
arr[row][col] = nowValue;
nowValue += 1;
}
nowDirectionIndex = (nowDirectionIndex + 1) % 3;
}
for (let i = 0; i < n; i += 1) {
for (let j = 0; j < n; j += 1) {
if (arr[i][j]) answer.push(arr[i][j]);
}
}
return answer;
};문제를 잘 해결하셨나요!
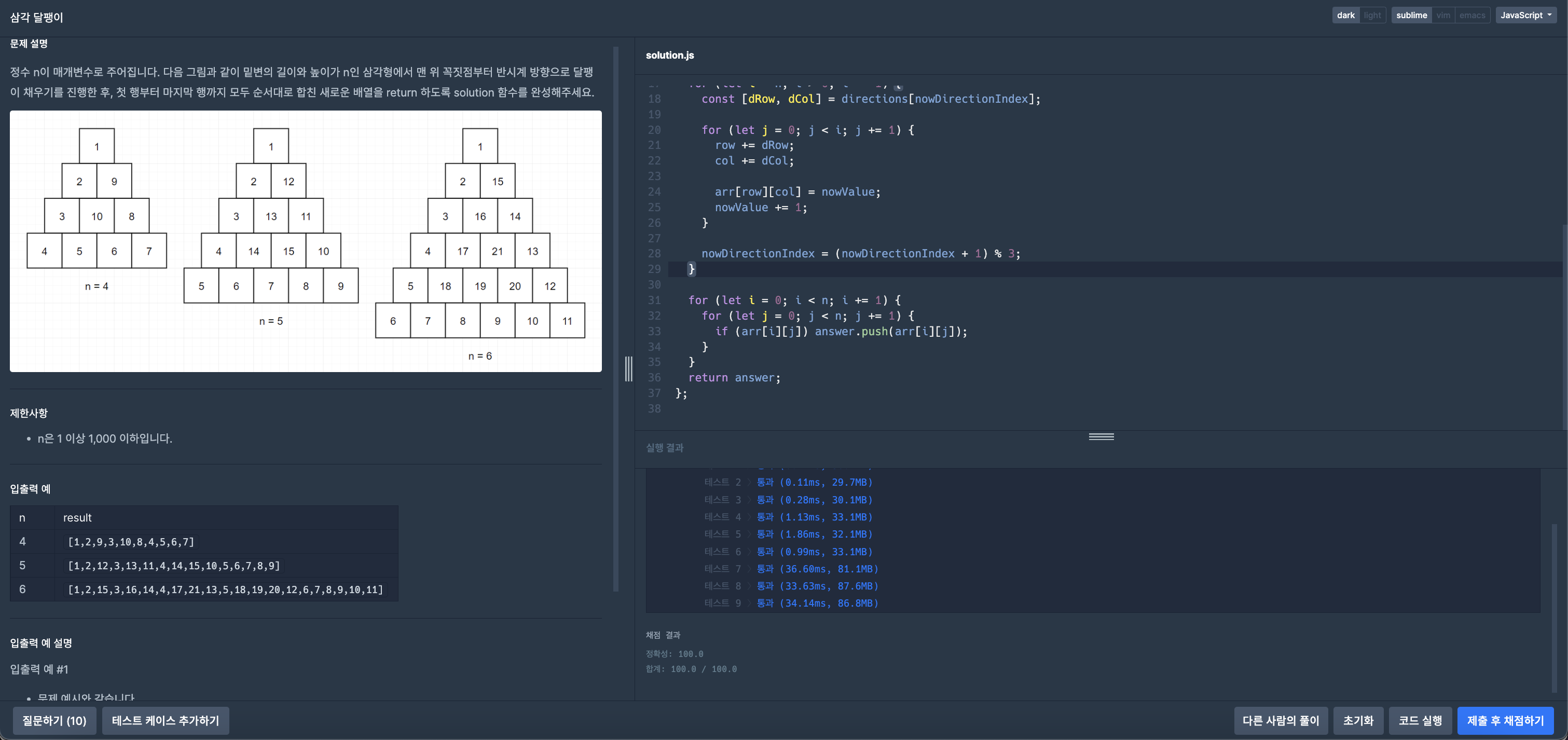
✨ 마치며
예전에는 배열을 반복문의 선언된 변수에 의존하지 않고 동적으로 할당하는 문제가 정말 어려웠는데, 연습하고 나니 이제는 10분 내로 해결이 가능하네요! 🙆🏻
확실히 알고리즘은, 반복적으로 훈련하는 게 중요한 것 같아요.
결국에 지금은 귀찮을지라도, 나중에는 몸이 기억하더라구요. 😆
다들, 현재의 자신을 믿고 꾸준히 알고리즘을 풀어나가봅시다. 이상! 🌈
.jpg)
저 이 문제 풀다가 넘 어려워서 블로그 서치중인데 재영님 블로그네요?! 너무 반가워서 댓글 남겨용 ㅎㅎㅎ 역시 글을 너무 잘쓰십니다 ..! 크..👍🏻👍🏻