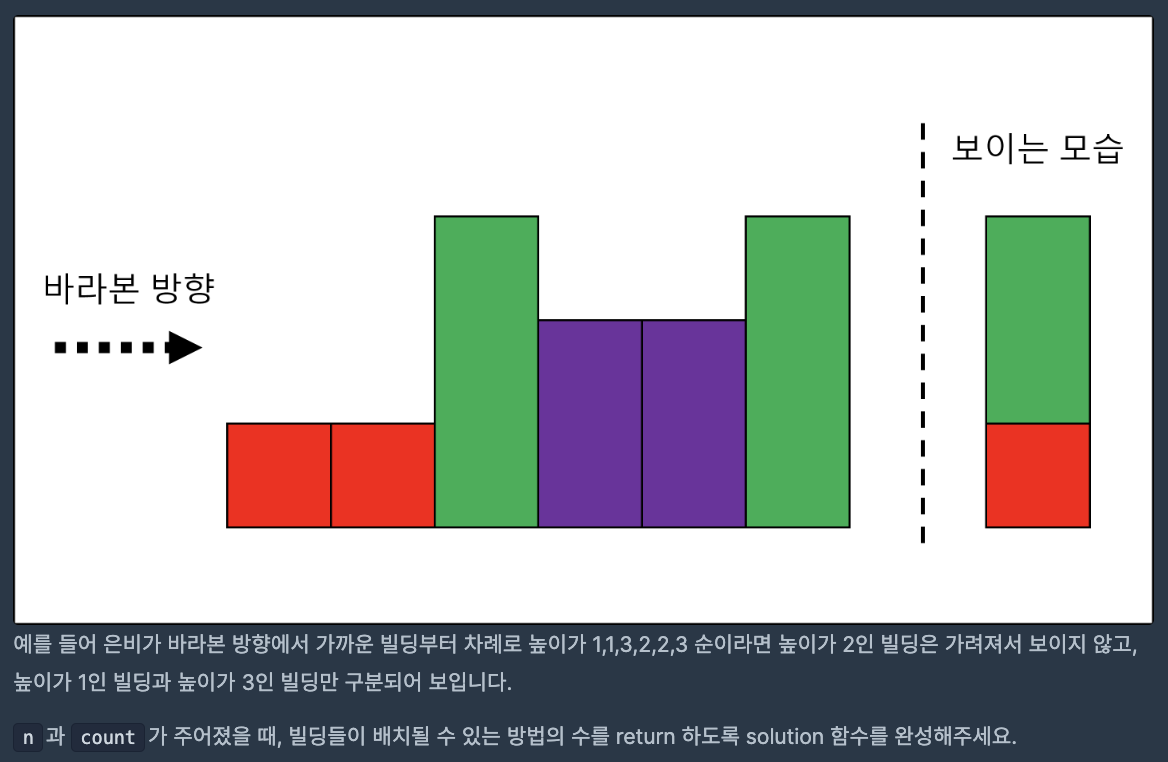
시작하며
최근에 알고리즘 스터디에서 제가 문제를 출제하게 됐습니다.
요새 저는 알고리즘 문제를 선별할 때 다음과 같은 생각으로 문제를 내고 있어요.
내가 해결할 수 있는 난이도보다 좀 더 어려운 문제를 내고 다같이 고민해보자!
이 기준은 항상 가변적이기는 하지만, 대개 정답률과 문제 내용을 보고 내는데요!
이 문제는 그런 의미에서 좀 더 탐났습니다.

오! Lv4에, 정답률이 5%라니! 문제를 정말 풀고 싶었어요.
그래서 문제를 보고, 약 2시간이 걸려 혼자서 문제를 해결하는 데 성공했습니다 😭
그럼, 어떻게 풀었는지 살펴볼까요?
문제 해결 과정
알고리즘 선택
DP vs Brute Force
n = 100입니다. 따라서 문제에 대한 시간복잡도를 좀 널널하게 가져갈 수 있지 않을까 싶었어요.
하지만 이 문제는 경우의 수를 따져야 하는 문제입니다. 또한, 조합의 문제가 아닌, 순열의 문제이지요.
정확히 말하자면 1~n에서의 순열은 아닙니다. 왜냐하면, 수 사이에 다른 수가 끼어있는 경우가 있기 때문입니다.
다만 같은 수들이, 다른 곳에 배치되면 서로 독립적인 것으로 인정된다는 관점에서 그냥 순열이라고 가정해봅시다!
따라서 이 문제를 Brute Force로 풀게 되면 얼마나 걸릴지 생각해봅시다.
- 전체 순열을 구한 다음,
- 반복문을 돌리고,
- 또 문자열을 반복해서
count가 일치하는지 찾은 다음 - 해당되는 배열의 개수를 구해야겠네요.
즉 어림 잡아봐도 약 O(N^2 * N!)이 걸린다는 무지막지한 결과가 나오겠군요!
공간복잡도 역시 저만큼은 나올 것 같아서, 수가 커질 수록 매우 부담이 크겠군요.
즉, 어떻게 봐도 최적의 답안이 아니며, 시간 초과 및 런타임 에러가 예상되기 때문에 보자마자 이 문제는 DP로 풀어야겠다고 생각했습니다.
어떻게 배열을 생성할 것인가
저는 이 문제를 보았을 때, 직관적으로 다음과 같이 메모이제이션을 할 배열을 생성했어요.
어떤 배열을
arr이라 할 때,
arr[A][B]=arr[n개][현재 count]=현재 n개 중에서 count개의 쌍둥이 빌딩이 나올 수 있는 경우의 수
또한, 점화식을 위한 함수는 다음과 같이 정의하겠습니다.
f(A, B)=현재 n개 중에서 count개의 쌍둥이 빌딩이 나올 수 있는 경우의 수
즉, arr[A][B] = f(A, B)라고 정의하겠습니다.
예를 들면, 문제에서 주어진 예시인 f(3, 1) = 8입니다.
어떻게 점화식을 생성할 것인가
쌍둥이 빌딩의 정의
결과적으로 쌍둥이 빌딩이라는 건, 다음과 같은 조건을 갖고 있어요.
n = 3일 때, 나올 수 있는 빌딩의 높이를
1,2,3이라고 하겠습니다.
- 빌딩은 항상 2쌍이 나와야 한다.
- 높은 빌딩 사이에는 더 높은 빌딩이 위치할 수 없다.
언뜻 봐서는 사실 점화식이 떠오르질 않아요.
그래서 더는 좀 더 그려보기로 했습니다. 바로 다음과 같이 말이죠!
문제 접근 1) n = 4일 때, 쌍둥이 빌딩이 가능한 경우의 수는 어떨까?
이를 하나하나 그리고, 답을 도출하기가 굉장히 까다로웠어요.
왜냐하면, 위에서 정의한, 높은 빌딩 사이에는 더 높은 빌딩이 위치할 수 없다.는 조건 때문이었어요.
글로 설명하면 이해가 되지 않을 것 같아 예시를 들어 볼게요.
n = 3, count = 2일 때 나올 수 있는 모든 경우의 수는 어느 값에 영향을 미칠까요?
막상 생각만 해도, 다음 3가지 케이스에 영향을 미치게 됩니다.
O(4,1)- 맨 앞에 높이가 4인 빌딩 쌍이 위치할 때O(4,2)- 맨 앞에 높이가1 || 2 || 3인 빌딩을 놓고, 뒤에 바로 높이가 4인 빌딩 쌍이 위치할 때O(4,3)- 높이가 4인 빌딩이 맨 뒤에 위치할 때
즉, 1개의 케이스가 이전/현재/다음까지 영향을 미치게 되는 점화식을 고른다?
이건 제게 너무 불합리하다고 생각했어요. f(n,c)라는 함수로부터 3개의 다른 함수 f(n+1, c-1), f(n+1, c) f(n+1, c+1)을 따지는 게 생각만 해도 너무 복잡하달까요? 😖
그래서 약 40분의 고민 끝에 다음과 같은 가설을 세웠어요. 바로 다음과 같이 말이죠.!
문제 접근 2) 이전의 식이, 다음 식에 영향이 미치는 정도를 최소화하자!
이를 위해 제가 접근한 문제의 접근 원리는 바로 이것입니다.
높이가 가장 작은 크기를
1이라 할 때,
11이라는 쌍둥이 빌딩을 하나하나의 빌딩 사이로 넣어서 도출해보는 건 어떨까?
이유는 다음과 같습니다.
11이 놓이는 경우는 굉장히 단순합니다! 이전의 빌딩 숲 중 아무데나 놓을 수 있기 때문이죠. 이는높은 빌딩 사이에는 더 높은 빌딩이 위치할 수 없다.는 조건을 언제든 만족할 수 있습니다.4인 빌딩의 쌍이 놓이는 경우의 수는44외에도41122334등 위치해야 할 곳을 찾기 까다로운데 반해,11을 찾는 로직으로 바꿔버리면 경우의 수를 찾기 쉽습니다.
따라서 만약 이전의 결과값이 332211이었다면, 저는 이를 443322로 해석하고, 11을 넣는 방법을 찾게 됐어요.
ex:
11443322,41143322,44113322,44311322, ...
즉, 어디에다가 더 큰 빌딩을 놓을지가 아닌, 어디에다가 더 작은 빌딩을 놓을지로 치환하여 문제를 풀어버린 셈이죠.
결과적으로 표를 볼까요? 다음과 같은 결과가 나옵니다.

어때요. 문제에 달려 있던 제약 조건을 다른 방법으로 단순화해버리니, 이제 표로 깔끔하게 정리할 수 있죠? 다만 아직 직관적으로 점화식이 와닿지 않아요. 이를 엑셀의 색상으로 경우의 수를 정리해볼게요.
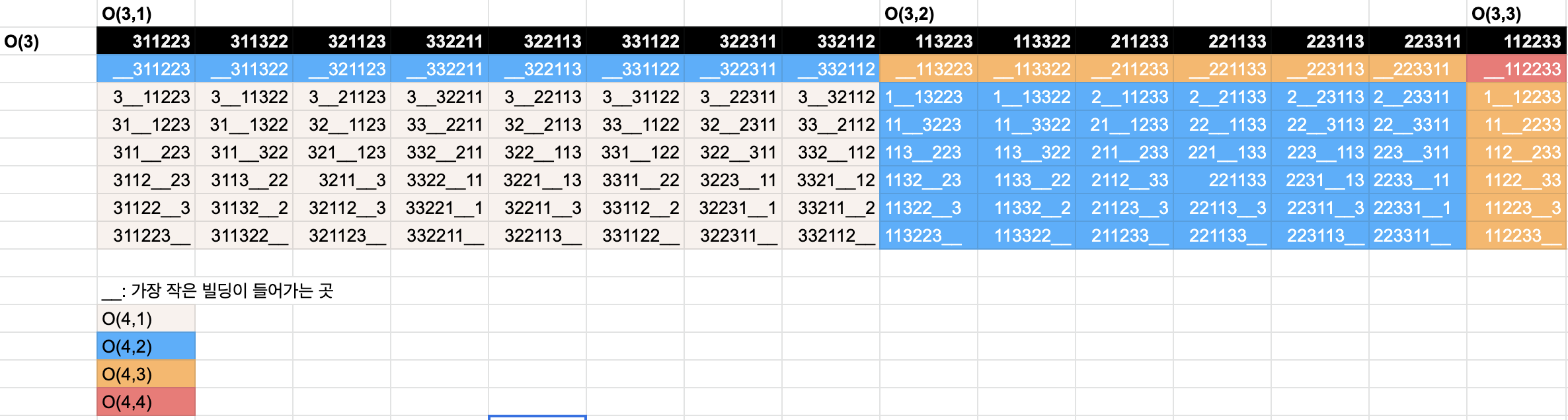
어?
뭔가 규칙이 보이지 않나요?
즉,
f(n, c)가 영향을 받는 곳은 다음과 같다고 할 수 있어요!
f(n-1, c-1)인 곳에서11을 맨 앞에 놓는 경우f(n-1, c)인 곳에서11을 맨 앞에 놓지 않는 경우
오! 엄청 문제에 대한 접근이 단순화되었어요.
이제 점화식을 생성할 수 있을 것 같아요. 바로 다음과 같이 말이죠!
// f(n, 0)인 경우는 0이라고 해석합니다. 왜냐하면, 그럴 경우는 존재하지 않기 때문이죠.
// 2(n-1): 이전 빌딩의 총 갯수를 의미해요 😉
// f(n, c) = f(n-1, c-1) + f(n-1, c) * 2(n-1)
arr[n][c] = arr[n-1][c-1] + 2 * (n - 1)* arr[n-1][c]이제 끝났네요. 최종적으로 문제를 풀어봅시다.
const MODULAR_ARITHMETIC_DIVIDE_NUMBER = 1000000007;
function solution(n, count) {
const arr = Array.from({ length: n + 1 }, () => new Array(n + 1).fill(0));
arr[1][1] = 1;
for (let row = 2; row < n + 1; row += 1) {
const prevRow = row - 1;
for (let col = 1; col <= row; col += 1) {
arr[row][col] =
(arr[prevRow][col - 1] + 2 * prevRow * arr[prevRow][col]) %
MODULAR_ARITHMETIC_DIVIDE_NUMBER;
}
}
return arr[n][count];
}
최적화
야호! 문제를 풀었어요 😆
하지만 저는 찝찝했어요. 결국 DP의 최대 단점은 쓸 데 없는 값까지 모두 계산해버린다는 점입니다.
문제를 굉장히 직관적으로 풀어냈지만, 더 효율적으로 풀 수 있을 것 같은 자신감이 들었어요.
어떻게 하면 문제를 최적화할 수 없을까?
결과적으로, 다음과 같은 엄청난 꼼수(?)를 발견하게 됩니다.
최적화 접근: 잠깐! count가 주어졌을 때, 더 큰 값을 계산할 필요가 있을까?
아까 우리가 도출했던 점화식의 조건이 무엇이었죠?
즉,
f(n, c)가 영향을 받는 곳은 다음과 같다고 할 수 있어요!
f(n-1, c-1)인 곳에서11을 맨 앞에 놓는 경우f(n-1, c)인 곳에서11을 맨 앞에 놓지 않는 경우
결과적으로 이것이 상징하는 것은, f(n-1, c+1)인 경우를 애초부터 고려할 필요가 없었다는 이야기이군요?
즉, 사소한 것일지라도, 어쨌든 계산을 하지 않는다는 것은 희소식이겠군요. 따라서 이를 다시 바꾸었습니다.
const MODULAR_ARITHMETIC_DIVIDE_NUMBER = 1000000007;
function solution(n, count) {
const arr = Array.from({ length: n + 1 }, () => new Array(count + 1).fill(0));
arr[1][1] = 1;
for (let row = 2; row < n + 1; row += 1) {
const prevRow = row - 1;
const nextColLength = Math.min(count, row);
for (let col = 1; col <= nextColLength; col += 1) {
arr[row][col] = (arr[prevRow][col - 1] + 2 * prevRow * arr[prevRow][col]) % MODULAR_ARITHMETIC_DIVIDE_NUMBER;
}
}
return arr[n][count];
}
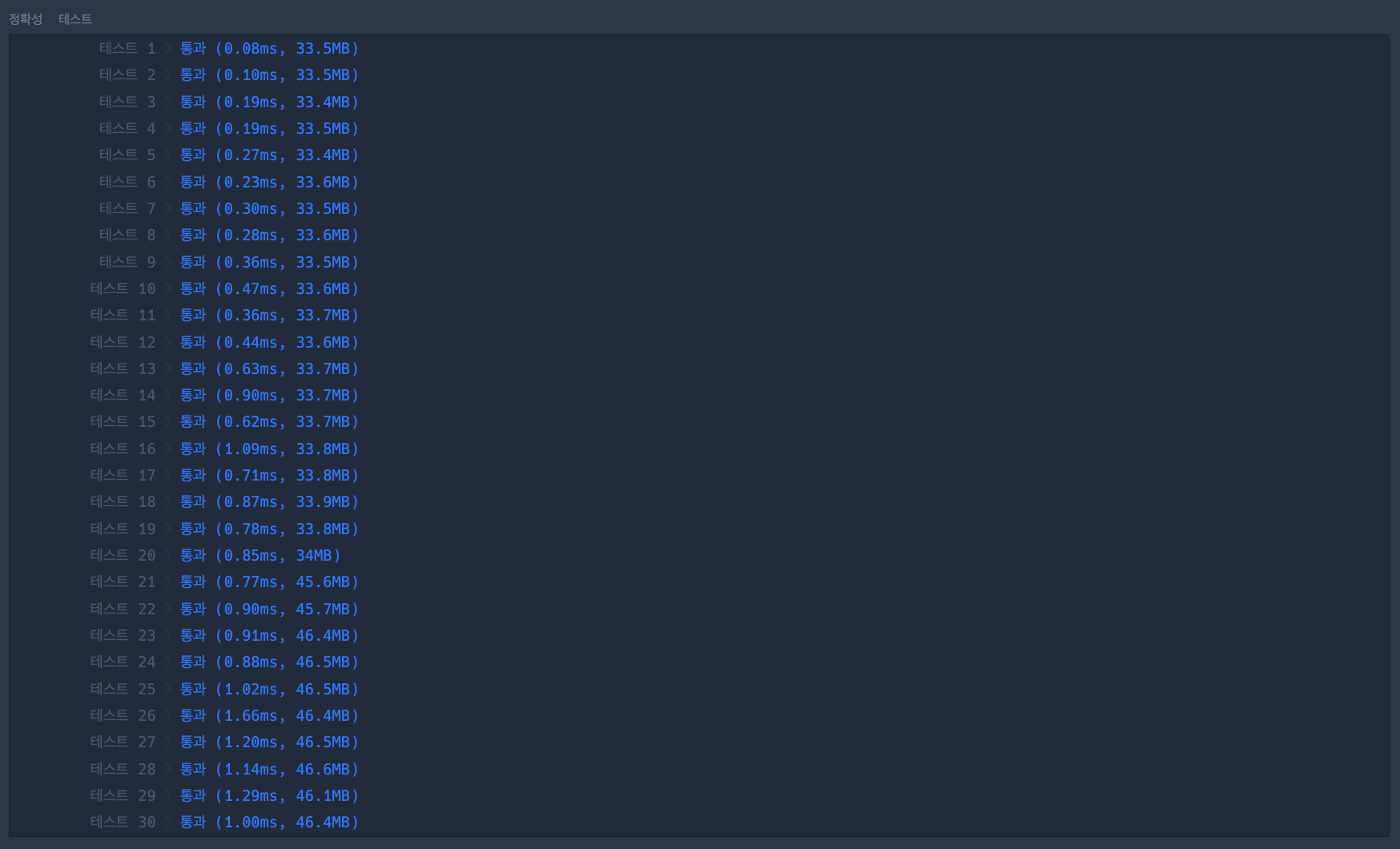
비교 결과
대충 n = 10000이고, 절반인 count = 5000의 경우를 비교해볼게요.
const MODULAR_ARITHMETIC_DIVIDE_NUMBER = 1000000007;
function before(n, count) {
const arr = Array.from({ length: n + 1 }, () => new Array(n + 1).fill(0));
arr[1][1] = 1;
for (let row = 2; row < n + 1; row += 1) {
const prevRow = row - 1;
for (let col = 1; col <= row; col += 1) {
arr[row][col] =
(arr[prevRow][col - 1] + 2 * prevRow * arr[prevRow][col]) %
MODULAR_ARITHMETIC_DIVIDE_NUMBER;
}
}
return arr[n][count];
}
const beforeStart = +new Date();
before(10000, 5000);
const beforeEnd = +new Date();
console.log(beforeEnd - beforeStart);
function after(n, count) {
const arr = Array.from({ length: n + 1 }, () => new Array(count + 1).fill(0));
arr[1][1] = 1;
for (let row = 2; row < n + 1; row += 1) {
const prevRow = row - 1;
const nextColLength = Math.min(count, row);
for (let col = 1; col <= nextColLength; col += 1) {
arr[row][col] = (arr[prevRow][col - 1] + 2 * prevRow * arr[prevRow][col]) % MODULAR_ARITHMETIC_DIVIDE_NUMBER;
}
}
return arr[n][count];
}
const afterStart = +new Date();
after(10000, 5000);
const afterEnd = +new Date();
console.log(afterEnd - afterStart);
console.log((beforeEnd - beforeStart) / (afterEnd - afterStart));결과는 다음과 같이 차이가 나는군요!

n = 100, count = 100인 경우에는 추가적인 연산으로 인해 효율성이 떨어질 수 있겠으나, 경우의 수가 늘어나고, 주어진 count가 작을 수록 분명 효율성이 더욱 증가될 것입니다.
그 중, count가 절반일 경우에는 약 1.33배의 성능 개선을 이루었습니다!
정리
이전의 방법: 최악-최선일 때의 시간 복잡도
O(NlogN)(2번째 반복문이row만큼 반복됩니다.)
이후의 방법: 최악 -O(NlogN), 최선 -O(N)(count = 1일 때)
결론
만약 직관적인 방법을 좋아하신다면, 최적화 하기 이전의 방법을 추천드려요.
모든 경우의 수가 계산되기 때문에, 다른 사람들에게 설명하기 적합할 것입니다 🙆🏻
하지만 나는 좀 더 효율적으로 문제에 접근하고 싶어!하시는 분들은 이후의 방법을 추천드려요.
이는 모든 경우의 수를 계산하지는 않기에 더 빠른 해답입니다 🙆🏻♀️
마치며
역시 생각보다 글을 쓴다는 것은 오랜 호흡이 걸리네요.
하지만 정말 글을 쓰고 나니, 제가 이 문제를 제대로 풀었다는 쾌감이 들어서 기분이 좋았어요.
요새 알고리즘 중 DP와 재귀함수에 많은 관심이 생기고 있어요.
chore한 계산 식을 컴퓨팅 사고 기반으로 해결한다는 점이 매력 있는 알고리즘이라는 생각이 들게끔 합니다. 너무 재밌어요 😆
비록 2시간이 걸렸지만... 그래도 오늘 또 한 걸음 성장했다는 뿌듯함에 기분이 좋군요!
이 글이 누군가에겐 도움이 되었으면 좋겠군요!
그럼 다들 즐거운 코딩하시길 바라며. 이상 :)
.jpg)