🌈 시작하며
점차 어려운 난이도에 익숙해지고자, 프로그래머스에서 lv4 문제를 풀어봤어요.
lv4 치고는 생각보다 난이도는 어렵지 않았는데, 문제의 조건이 쉽게 주어져서 그랬던 것 같아요 🙆🏻
어떤 문제였는지, 어떻게 포인트를 잡고 풀어나갔는지를 한 번 살펴보죠!
🔍 본론
문제 정의
일단, 저는 다음과 같은 흐름으로 문제의 요지를 파악해나갔어요.
l번 바구니부터 m번 바구니까지, 둘째 아들에게는 m+1번 바구니부터 r번 바구니까지를 주려합니다.
여기서 든 생각은, '음... 기준점을 따로 잡아야겠네.' 였습니다.
알고리즘을 풀 때 제가 접근하는 방법은, 내가 어떤 문제를 해결하기 위해 우선적으로 무엇을 구해야 하는지이기 때문에 저는 다음과 같은 핵심 문제를 정의했습니다.
문제의 해에 도달하기 위한
lmr의 최적의 값은 무엇인가.
문제 조건
그렇다면 이제 해당 값을 찾아내기 위해 조건 값이 있겠죠?
이를 한 번 탐색해나가봅시다.
단, 두 아들이 받을 과자 수는 같아야 합니다(1 <= l <= m, m+1 <= r <= N). 즉, A[i] 를 i번 바구니에 들어있는 과자 수라고 했을 때, A[l]+..+A[m] = A[m+1]+..+A[r] 를 만족해야 합니다.
오...! 그냥 두 형제가 받을 값이 같으면 되겠네요.
즉 다음과 같이 세울 수 있겠죠?
[[l ~ m번째의 합]]=[[ m + 1 ~ r번째의 합]]
해결 방법 설계
따라서 저는 이 두 조건을 갖고 해결 방법을 탐색했어요.
일단 저는 가장 눈여겨 봤던 알고리즘은 바로 구간합을 사용할 수 있지 않을까였어요.
결국 각 구간의 합을 지속해서 계산하는 것은 비효율적인 것 같아서, 구간합 알고리즘을 우선 사용했습니다. 구현도 간단하니까요!
// 구간합을 구하는 함수 생성
const getPrefixSum = (arr) => {
const arrLength = arr.length;
const arrPrefixSum = new Array(arrLength + 1).fill(0);
for (let i = 0; i < arrLength; i += 1) {
const now = arr[i];
arrPrefixSum[i + 1] = now + arrPrefixSum[i];
}
return arrPrefixSum;
};참고로 저는, i + 1번째까지 만들어서 memoization을 쉽게 하도록 만들었답니다 👐🏻 혹여나 참고해주세요!
그러면 이제 구간합을 구했으니, l m r을 찾아야겠군요?
저는 여기서 투 포인터를 이용했어요.
👀 잠깐, 투 포인턴데, 이건 3개의 변수를 업데이트해야 하는데요?
그럼 쓰리 포인터로... 크... 크흡
여기서 저는 투 포인터를 좀 특이하게 쓰려고 합니다. 바로 for문을 한 번 wrapping해주는 건데요.
어차피 기준점은 선상에서 존재하며, 여기서 l r이 유동적으로 움직입니다. 그리고 기준점을 토대로 서로 그 범위를 넘길 수 없죠.
따라서 m을 기준으로 for문을 돌립니다. 이때, m + 1이 넘어가지 않도록, cookie.length - 1까지만 돌아가면 되겠죠?
for (let m = 0; m < cookieLength - 1; m += 1) {
const leftEnd = m;
const rightStart = m + 1;
let leftStart = leftEnd; // l
let rightEnd = rightStart; // r
...
}자, 이렇게 하면 이제 우리는 저 투 포인터를 요리조리 돌려가며, 문제의 조건에 부합하는 답을 찾으면 됩니다.
일단 위의 반복문 안에, 왼쪽의 구간합과 오른쪽의 구간합을 비교하는 로직을 써줍시다.
let nowLeftSum = cookiePrefixSum[m + 1] - cookiePrefixSum[leftStart];
let nowRightSum = cookiePrefixSum[rightEnd + 1] - cookiePrefixSum[m + 1];그러면 이제 이 값을 토대로 왼쪽을 갈지, 오른쪽을 갈지 판단해주면 되는데요.
아! 여기서 제가 설명해주지 않은 것이 있어요.
이 투 포인터가 이렇게 간단하게 가능한 이유는 cookie의 각각의 원소는 1 이상 500 이하인 자연수입니다.라는 조건이 있기 때문입니다.
만약 자연수가 아니라면, 어느 쪽을 움직여야할지 감이 안잡히므로, 해시라도 써서 이 답을 구해야 했을 것이고, 더 복잡해졌을 거에요!
다행히도 문제의 제한 사항이 친절했기에, 감지덕지하면서 구해주면 되겠네요 😁
if (nowLeftSum === nowRightSum) {
result = Math.max(nowLeftSum, result);
rightEnd += 1;
leftStart -= 1;
} else if (nowLeftSum < nowRightSum) {
leftStart -= 1;
} else {
rightEnd += 1;
}전체 코드
시간 복잡도
음...
- 구간합에서
O(N) for문에서O(N)- while문에서
O(N)(최악의 경우)
총 O(N) + O(N) * O(N) = O(N^2)겠군요!
// 구간합을 구하는 함수 생성
const getPrefixSum = (arr) => {
const arrLength = arr.length;
const arrPrefixSum = new Array(arrLength + 1).fill(0);
for (let i = 0; i < arrLength; i += 1) {
const now = arr[i];
arrPrefixSum[i + 1] = now + arrPrefixSum[i];
}
return arrPrefixSum;
};
const solution = (cookie) => {
if (cookie.length === 1) return 0;
let result = 0;
const cookiePrefixSum = getPrefixSum(cookie);
const cookieLength = cookie.length;
// 기준점 이동시키기
for (let m = 0; m < cookieLength - 1; m += 1) {
const leftEnd = m;
const rightStart = m + 1;
let leftStart = leftEnd;
let rightEnd = rightStart;
while (leftStart >= 0 && rightEnd < cookieLength) {
let nowLeftSum = cookiePrefixSum[m + 1] - cookiePrefixSum[leftStart];
let nowRightSum = cookiePrefixSum[rightEnd + 1] - cookiePrefixSum[m + 1];
if (nowLeftSum === nowRightSum) {
result = Math.max(nowLeftSum, result);
rightEnd += 1;
leftStart -= 1;
} else if (nowLeftSum < nowRightSum) {
leftStart -= 1;
} else {
rightEnd += 1;
}
}
}
return result;
};
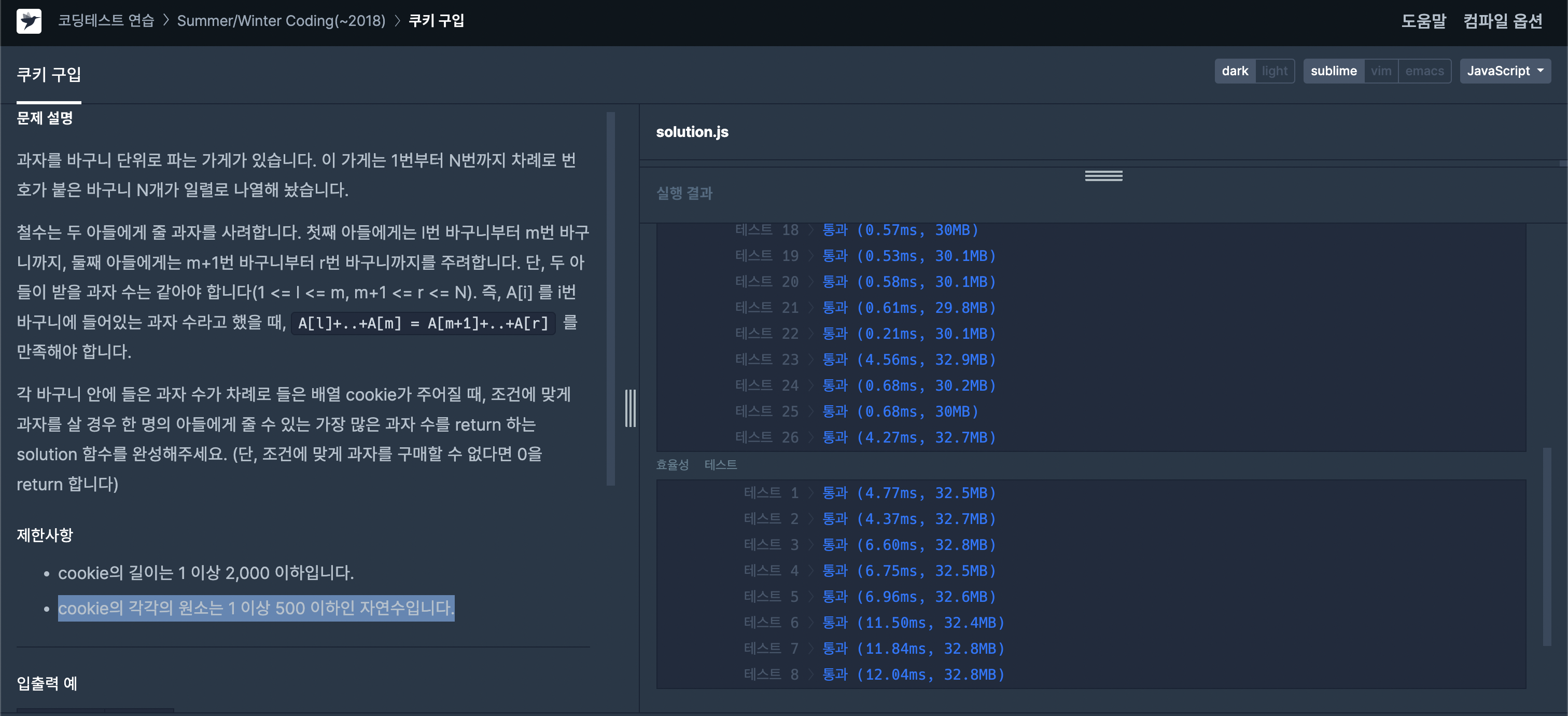
결과
짜잔. 효율성에서 큰 걱정 없이 통과하는 군요. 어썸합니다. 😉
🔥 마치며
최근에 심했던 슬럼프를 이겨내고, 다시 문제를 푸니 더 잘 되는 것 같아요.
앞으로도 꾸준히 공부하는 과정들을 업로드하려 합니다!
방법이 궁금했던 분들께 좋은 코드였길 바라며, 그럼 즐거운 코딩하시길 바라요. 🚀
.jpg)