[자료구조] 레드 블랙 트리 / Red-Black Tree (+ c 언어로 구현하기)
🔴 ⚫️ 레드 블랙 트리란?
레드 블랙 트리는 자가 균형 이진 탐색 트리(self-balancing binary search tree)의 일종으로, 노드의 색상을 사용하여 트리의 균형을 유지하는 것이 특징이다.
레드 블랙 트리는 아래의 다섯 가지 속성을 반드시 충족해야 한다.
🖐 레드 블랙트리의 다섯 가지 속성
1. 모든 노드는 빨간색 또는 검은색이다.
2. 루트 노드는 항상 검은색이다.
3. 모든 단말노드(leaf, NIL)은 검은색이다.
4. 빨간색 노드의 자식 노드는 반드시 검은색이다.
5. 각각의 노드에서 NIL 노드까지 이르는 단순 경로들은 동일한 수의 검은색 노드를 포함한다.

😲 레드 블랙 트리를 왜 사용할까?
레드 블랙 트리의 필요성은 이진 탐색 트리 (Binary Search Tree)의 한계점과 관련이 있다.
이진 탐색 트리는 데이터를 정렬된 상태로 저장하여 일반적으로 빠른 탐색이 가능하다.
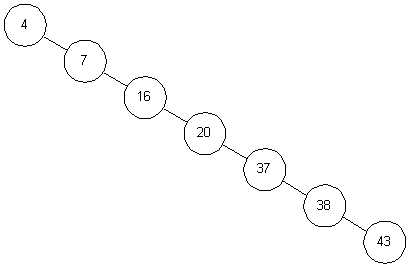
하지만 최악의 경우 아래 그림과 같이 정렬된 순서로 데이터가 삽입이 되면, 사실상 연결 리스트와 동일한 형태가 되어 탐색에 선형 시간(O(n))이 소요된다.
이러한 문제를 해결하기 위해 균형 이진 탐색 트리 (Balanced Binary Search Tree)가 등장했다.
균형 이진 탐색 트리는 삽입, 삭제 작업을 수행할 때마다 자동으로 균형을 유지해서, 최악의 경우에도 탐색 시간이 O(log n)이 되도록 보장한다.
레드 블랙 트리는 균형 이진 탐색 트리의 일종으로 데이터 삽입, 삭제, 탐색의 효율성을 보장한다는 장점이 있다.
🧩 레드 블랙 트리의 구성 요소
레드 블랙 트리의 노드는 일반적으로 아래와 같이 다섯 가지 요소로 구성된다.
/*
1. 노드의 색상
2. 노드의 키 값
3. 부모 노드의 포인터
4. 왼쪽 자식 노드의 포인터
5. 오른쪽 자식 노드의 포인터
*/
typedef struct node_t {
color_t color;
key_t key;
struct node_t *parent, *left, *right;
} node_t;레드 블랙 트리는 루트 노드와 NIL 노드로 구성할 수 있다.
typedef struct {
node_t *root;
node_t *nil; // for sentinel
} rbtree;🤔 NIL 노드란?
Sentinel은 데이터 구조의 끝을 나타내는 데에 사용하는 것을 의미하는데, 레드 블랙 트리의 경우 트리의 말단을 나타내는 Sentinel로서 NIL 노드가 사용된다.
NIL 노드를 사용했을 때의 장점은 삽입, 삭제 등의 연산들 수행할 때 NULL 포인터 체크를 하지 않아도 된다는 점이다.
NIL 노드는 무조건 검은색이므로 아래와 같이 초기화한다.
// NIL 노드 포인터
node_t *nil = (node_t *)calloc(1, sizeof(node_t));
if (nil == NULL)
{
free(p);
return NULL;
}
// NIL 노드 값 초기화
nil->color = RBTREE_BLACK;
nil->key = 0;
nil->parent = NULL;
nil->left = NULL;
nil->right = NULL;⚖️ 레드 블랙 트리의 균형 유지하기
데이터 삽입, 삭제 등을 진행하다보면 레드 블랙 트리의 충족 요건이 깨질 수 있는데, 이때는 색상 변경과 회전을 통해 다시 요건을 충족하도록 만들 수 있다.
이러한 과정을 거치면서 레드 블랙 트리의 균형은 항상 유지될 수 있다.
레드 블랙 트리의 균형을 유지시키는 방법에 대해 다음 절에서 더 자세히 살펴보자.
🔄 회전 (Rotations)
레드 블랙 트리의 포인터 구조는 회전을 통해 변경되는데, 아래와 같이 왼쪽 회전 방식과 오른쪽 회전 방식이 있다.
왼쪽 회전은 오른쪽으로 치우친 구조를 왼쪽으로 옮기고, 오른쪽 회전은 왼쪽으로 치우친 구조를 오른쪽으로 옮겨줘서 트리의 균형을 유지할 수 있도록 한다.
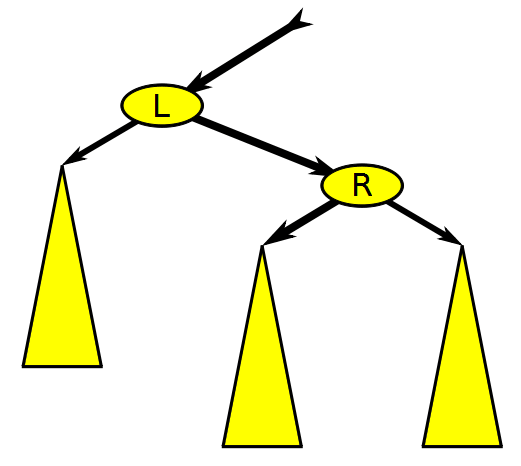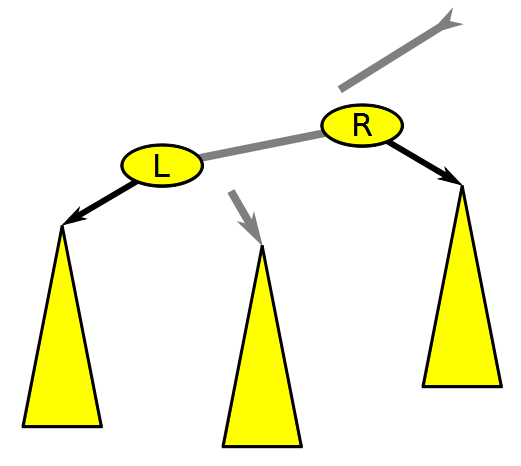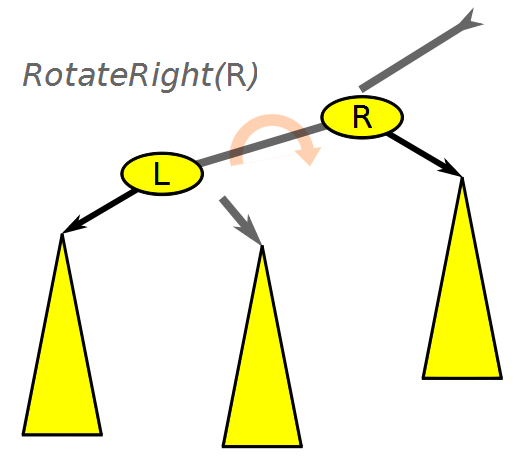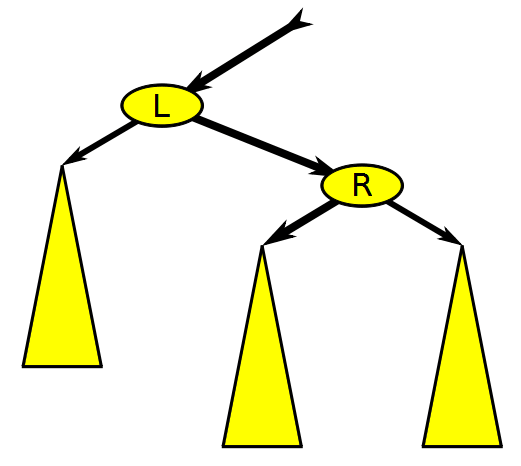
아래 코드는 왼쪽 회전 코드이고, 오른쪽 회전을 시키려면 방향만 반대로 바꾸면 된다.
🔻 왼쪽 회전 코드
void left_rotate(rbtree *t, node_t *x)
{
// x는 아래로 내려가는 노드, y는 위로 올라가는 노드
node_t *y = x->right;
// y의 왼쪽 서브트리를 x의 오른쪽 서브트리로 옮김
x->right = y->left;
if (y->left != t->nil)
{
y->left->parent = x;
}
y->parent = x->parent;
// 만약 x가 루트 노드였다면 트리의 루트 노드를 y로 변경
if (x->parent == t->nil)
{
t->root = y;
}
// x의 부모가 x 대신 y를 자식 노드로 바라보도록 수정
else if (x == x->parent->left)
{
x->parent->left = y;
}
else
{
x->parent->right = y;
}
// x를 y의 왼쪽 자식 노드로 변경
y->left = x;
// x의 부모 노드를 y로 변경
x->parent = y;
}➕ 삽입 (Insertions)
새로 추가하는 노드의 색상은 빨간색이고, 검은색 NIL 노드를 두 개 가지고 있어야 한다.
노드를 삽입하는 방식은 일반 Binary Search Tree와 동일한데, 노드를 삽입한 후 레드 블랙 트리의 속성을 위반했을 때 재조정 작업을 거친다는 점이 다르다.
rbtree_insert(노드 삽입 함수)와 rb_insert_fixup(노드 삽입 후 트리 재조정 함수) 코드를 먼저 본 후, 관련 내용을 좀 더 자세히 살펴보자.
🔻 노드 삽입 함수
/*
🔴⚫️ RB 트리에 새로운 노드를 삽입하는 함수
*/
node_t *rbtree_insert(rbtree *t, const key_t key)
{
// 새로 추가할 노드 메모리 할당하기
struct node_t *new_node = calloc(1, sizeof(struct node_t));
// 메모리 할당에 실패한 경우 NULL 리턴
if (new_node == NULL)
{
return NULL;
}
// 새로 추가할 노드 값 초기화
new_node->color = RBTREE_RED;
new_node->key = key;
new_node->parent = t->nil;
new_node->left = t->nil;
new_node->right = t->nil;
// 만약 트리가 비어있는 상태라면 루트 노드를 추가하고 리턴하기
if (t->root == t->nil)
{
t->root = new_node;
t->root->color = RBTREE_BLACK; // 루트노드는 검은색
return new_node;
}
struct node_t *curr = t->root; // 새로 추가할 노드와 비교할 노드
struct node_t *prev = t->nil; // 새로 추가할 노드의 부모가 될 노드
// sentinel 노드에 이를 때까지 내려가기
while (curr != t->nil)
{
prev = curr;
if (key < curr->key)
{ // 넣으려는 값이 현재 노드의 값보다 작은 경우
curr = curr->left; // 왼쪽 노드로 포커스 이동
}
else
{ // 넣으려는 값이 현재 노드의 값보다 크거나 같은 경우
curr = curr->right; // 오른쪽 노드로 포커스 이동
}
}
// 노드를 추가할 위치를 찾은 경우 새로 추가할 노드의 부모 노드 설정
new_node->parent = prev;
// 부모 노드의 왼쪽 자식 또는 오른쪽 자식으로 추가
if (new_node->key < prev->key)
{
prev->left = new_node;
}
else
{
prev->right = new_node;
}
// 노드 삽입 후 RB 트리 속성을 위반한다면 재조정
rb_insert_fixup(t, new_node);
return new_node;
}
🔻 노드 삽입 후 트리 재조정 함수
void rb_insert_fixup(rbtree *t, node_t *node)
{
// 노드가 루트 노드가 아니고 부모 노드의 색깔이 빨간색일 때까지 반복문 진행
while (node != t->root && node->parent->color == RBTREE_RED)
{
// 부모 노드가 할아버지 노드의 왼쪽 자식인 경우
if (node->parent == node->parent->parent->left)
{
node_t *uncle = node->parent->parent->right;
// Case 1. 부모 노드와 삼촌 노드의 색깔이 빨간색인 경우
if (uncle != NULL && uncle->color == RBTREE_RED)
{
node->parent->color = RBTREE_BLACK;
uncle->color = RBTREE_BLACK;
node->parent->parent->color = RBTREE_RED;
node = node->parent->parent; // 할아버지 노드로 포커싱 이동
}
else
{
// Case 2. 삼촌 노드는 검은색이고 현재 노드가 오른쪽 자식인 경우
if (node == node->parent->right)
{
node = node->parent;
left_rotate(t, node);
}
// Case 3. 삼촌 노드는 검은색이고 현재 노드가 왼쪽 자식인 경우
else
{
node->parent->color = RBTREE_BLACK;
node->parent->parent->color = RBTREE_RED;
right_rotate(t, node->parent->parent);
}
}
}
// 부모 노드가 할아버지 노드의 오른쪽 자식인 경우
else
{
node_t *uncle = node->parent->parent->left;
// Case 4. 부모 노드와 삼촌 노드의 색깔이 빨간색인 경우
if (uncle != NULL && uncle->color == RBTREE_RED)
{
node->parent->color = RBTREE_BLACK;
uncle->color = RBTREE_BLACK;
node->parent->parent->color = RBTREE_RED;
node = node->parent->parent; // 할아버지 노드로 포커싱 이동
}
else
{
// Case 5. 삼촌 노드는 검은색이고 현재 노드가 왼쪽 자식인 경우
if (node == node->parent->left)
{
node = node->parent;
right_rotate(t, node);
}
// Case 6. 삼촌 노드는 검은색이고 현재 노드가 오른쪽 자식인 경우
else
{
node->parent->color = RBTREE_BLACK;
node->parent->parent->color = RBTREE_RED;
left_rotate(t, node->parent->parent);
}
}
}
}
t->root->color = RBTREE_BLACK;
}👉🏻 반복문 설정 방법
위의 트리 재조정 함수를 살펴보면 현재 노드가 루트 노드가 아니고 현재 노드의 부모 노드 색상이 빨간색일 때까지 반복문을 진행한다.
루트 노드의 부모 노드는 검은색인 NIL 노드이므로, 위 반복문의 조건은 다시 말해 부모 노드의 색상이 빨간색일 때까지 반복을 진행하겠다는 의미라 할 수 있다.
새로 추가되는 노드는 빨간색이므로, 부모 노드의 색상이 빨간색이면 레드 블랙 트리의 요건 4️⃣번(= 빨간색 노드의 자식 노드는 반드시 검은색이다)을 위반한다.
따라서 반복문을 아래와 같이 설정한 것은 부모 노드의 색상이 검은색이 되어서 레드 블랙 트리의 요건을 충족할 때까지 트리 재조정을 진행하기 위함이다.
👉🏻 각 경우의 수
삽입 후 트리를 재조정 할 때 고려하는 경우의 수는 여섯 가지이다.
부모 노드가 할아버지 노드의 왼쪽 자식인 경우와 오른쪽인 경우는 방향만 반대로 바꿔주면 되므로, 부모 노드가 할아버지 노드의 왼쪽 자식인 경우에 해당되는 세 가지 경우의 수만 살펴보자.
(1) 부모 노드와 삼촌 노드의 색깔이 모두 빨간색인 경우
부모와 삼촌의 색깔을 검은색으로 바꾸고, 할아버지의 색깔을 빨간색으로 바꾼 다음 할아버지 노드로 초점을 옮긴다.
아래의 예시를 보면 노드 11이 삽입되었을 때 먼저 부모와 삼촌을 검은색으로, 할아버지를 빨간색으로 변경한다.
그리고 할아버지 노드로 초점을 이동하여 다음 반복문을 진행하면, 현재 노드가 루트에 위치하므로 루트 노드를 검은색으로 변경하고 재조정 작업을 완료한다.
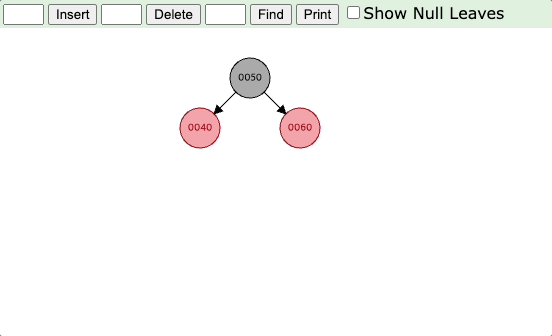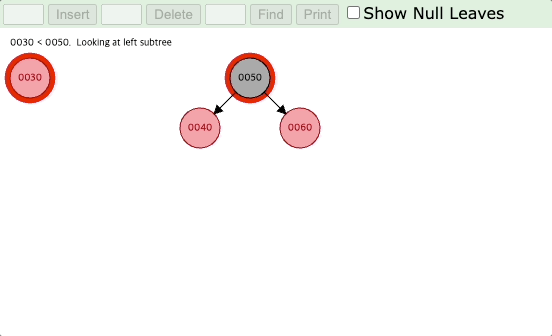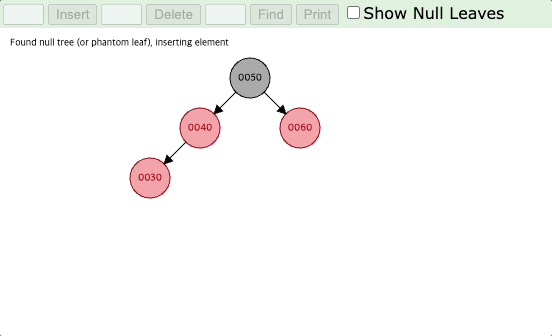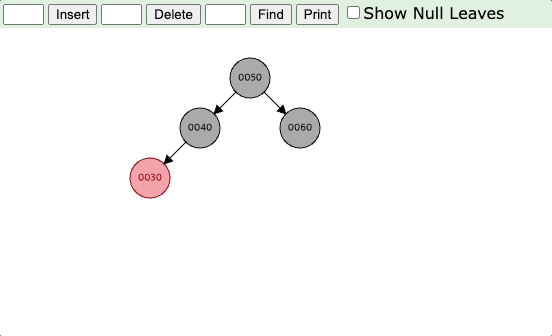
(2) 삼촌 노드는 검은색이고, 현재 노드가 오른쪽 자식 노드인 경우
부모 노드로 초점을 옮긴 다음, 부모 노드를 기준으로 왼쪽으로 회전시킨다.
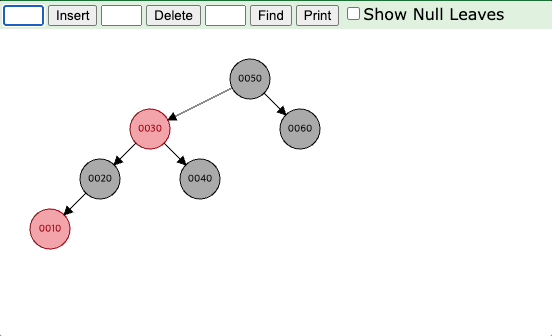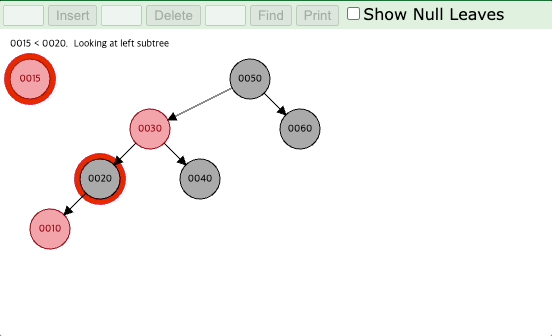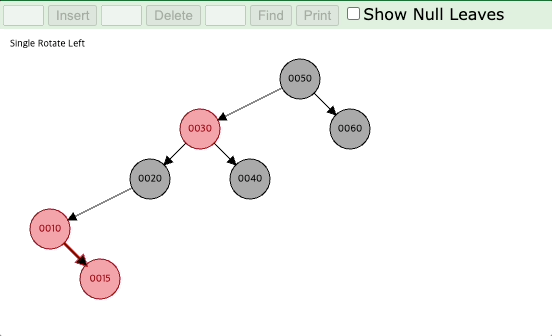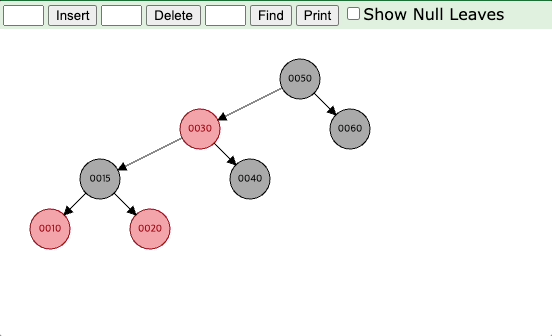
아래의 예시를 보면 먼저 15가 들어왔을 때, 15는 10의 오른쪽 자식 노드로 들어가게 된다.
그러면 10의 형제 노드는 NIL 노드로 검은색이므로 (2)번 경우에 해당되어 부모 노드 10을 기준으로 왼쪽으로 회전을 시킨다.
왼쪽으로 회전을 시키고 나면 아래에서 살펴볼 (3)번 경우에 해당되어서 (3)번 경우의 작업을 거치고 나면 레드 블랙 트리의 요건을 충족하게 된다.
(3) 삼촌 노드는 검은색이고 현재 노드가 왼쪽 자식인 경우
부모의 색상을 검은색으로, 할아버지의 색상을 빨간색으로 변경한 후, 부모 노드를 기준으로 오른쪽으로 회전시킨다.
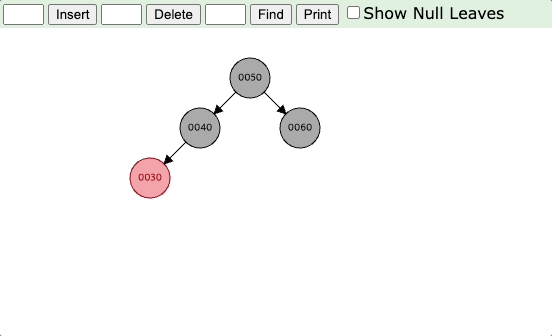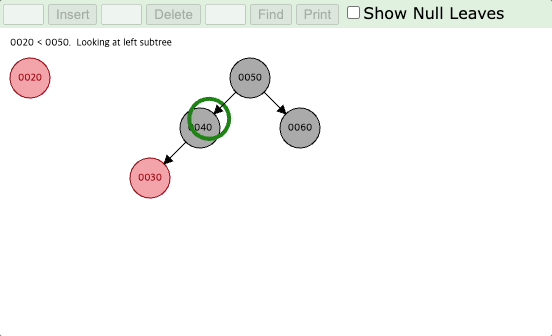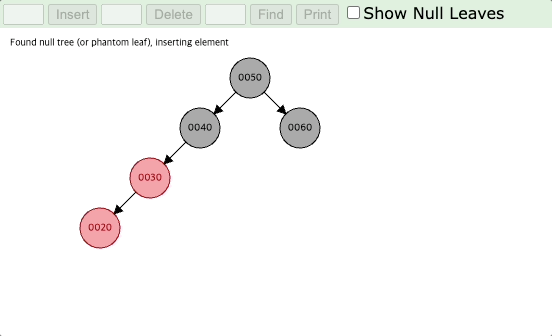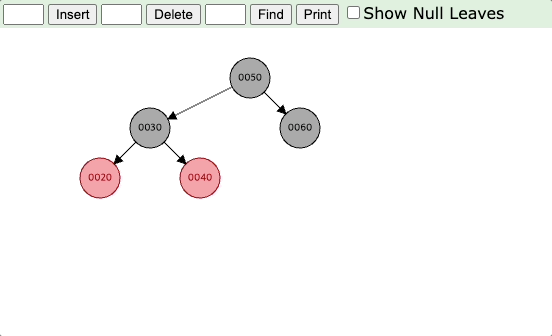
아래 예시의 경우 20이 들어오면 30의 왼쪽 자식 노드가 되고, 삼촌 노드는 NIL 노드이므로 (3)번 케이스에 해당된다.
부모 노드인 30을 기준으로 회전을 시키면 양쪽 높이의 균형이 맞춰지게 되고, 부모 노드의 색상과 할아버지 노드의 색상을 바꿔주면 black depth도 맞춰지게 된다.
➖ 삭제 (Deletion)
삭제 또한 Binary Search Tree와 삭제 방식이 동일하고, 삭제한 이후 레드 블랙 트리의 속성이 깨졌다면 재조정 작업을 거친다.
이때 빨간색 노드는 삭제를 해도 레드 블랙 트리의 속성에 영향을 미치지 않지만, 검은색 노드를 삭제하면 레드 블랙 트리 속성이 깨지게 할 수 있다.
왜 빨간색 노드는 삭제해도 레드 블랙 트리의 속성이 유지될까?
빨간색 노드의 삭제는 트리의 black-height와 각 노드의 black-depth에 영향을 미치지 않고, 빨간색 노드의 부모, 자식은 모두 검은색이므로 삭제해도 빨간색 노드끼리 인접할 일이 없기 때문이다.
rbtree_erase(노드 삭제 함수)와 delete_fixup(노드 삭제 후 트리 재조정 함수)의 코드를 먼저 본 후, 관련 내용을 좀 더 자세히 살펴보자.
🔻 노드 삭제 함수
/*
🔴⚫️ RB 트리에서 인자로 주어진 노드를 삭제하고 메모리를 반환하는 함수
*/
int rbtree_erase(rbtree *t, node_t *p)
{
node_t *del = p; // 삭제할 노드 y
color_t original_color = del->color; // 삭제할 노드의 원래 색상
node_t *base; // 트리 재조정의 기준점이 될 노드 x
if (p->left == t->nil)
{
base = p->right;
// p를 p의 오른쪽 자식 노드로 대체
transplant(t, p, p->right);
}
else if (p->right == t->nil)
{
base = p->left;
// p를 p의 왼쪽 자식 노드로 대체
transplant(t, p, p->left);
}
else
{
del = tree_minimum(t, p->right); // successor 찾기
original_color = del->color;
base = del->right;
// 만약 successor가 p의 오른쪽 자식 노드가 아닌 경우
if (del != p->right)
{
// successor을 successor의 오른쪽 sub tree로 교체
transplant(t, del, del->right);
del->right = p->right;
del->right->parent = del;
}
else
{
// base(successor의 오른쪽 자식 노드)가 nil 노드인 경우를 위해 parent 값 설정해주기
base->parent = del;
}
transplant(t, p, del);
del->left = p->left;
del->left->parent = del;
del->color = p->color;
}
// 삭제하려는 노드의 메모리 해제하기
free(p);
// 검은색 노드를 삭제한 경우 RB 트리 속성이 깨질 수 있으므로 재조정 작업하기
if (original_color == RBTREE_BLACK)
{
delete_fixup(t, base);
}
return 0;
}🔻 노드 삭제 후 트리 재조정 함수
/*
🔴⚫️ 노드 삭제 후 RB 트리의 속성을 충족할 수 있도록 재조정하는 함수
*/
void delete_fixup(rbtree *t, node_t *x)
{
// while문에서 x는 항상 non-root doubly black node
while (x != t->root && x->color == RBTREE_BLACK)
{
if (x == x->parent->left)
{
node_t *w = x->parent->right;
// Case 1. x의 형제 w가 빨간색 노드일 때
if (w->color == RBTREE_RED)
{
// w의 색상과 x->parent의 색상을 교환
w->color = RBTREE_BLACK;
x->parent->color = RBTREE_RED;
left_rotate(t, x->parent);
w = x->parent->right;
// => 이 과정을 마치면 Case 2, 3, 4 중 하나에 해당하게 됨
}
// Case 2. x의 형제 w가 검은색 노드이고, w의 자식들이 모두 검은색 노드일 때
if (w->left->color == RBTREE_BLACK && w->right->color == RBTREE_BLACK)
{
w->color = RBTREE_RED;
x = x->parent;
}
else
{
// Case 3. x의 형제 w가 검은색 노드이고, w의 왼쪽 자식은 빨간색 노드, w의 오른쪽 자식은 검은색 노드일 때
if (w->right->color == RBTREE_BLACK)
{
// w의 색상과 w->left의 색상을 교환한 다음 오른쪽 회전
w->left->color = RBTREE_BLACK;
w->color = RBTREE_RED;
right_rotate(t, w);
w = x->parent->right;
// => 이 과정을 마치면 Case 4.로 가게 됨
}
// Case 4. x의 형제 w가 검은색 노드이고, w의 오른쪽 자식이 빨간색 노드일 때
w->color = x->parent->color;
x->parent->color = RBTREE_BLACK;
w->right->color = RBTREE_BLACK;
// x->parent를 기준으로 왼쪽으로 회전하여 x에 있는 extra black 제거
left_rotate(t, x->parent);
// x를 루트로 변경하여 while문 종료
x = t->root;
}
}
else
{
node_t *w = x->parent->left;
// Case 5. x의 형제 w가 빨간색 노드일 때
if (w->color == RBTREE_RED)
{
w->color = RBTREE_BLACK;
x->parent->color = RBTREE_RED;
right_rotate(t, x->parent);
w = x->parent->left;
}
// Case 6. x의 형제 w가 검은색 노드이고, w의 자식들이 모두 검은색 노드일 때
if (w->right->color == RBTREE_BLACK && w->left->color == RBTREE_BLACK)
{
// doubly black이었던 x를 검은색 노드 하나만 가지고 있게 하고, w는 빨간색 노드로 변경함
w->color = RBTREE_RED;
// x와 w가 검은색 노드를 읽은 것을 보상하기 위해 x->parent에 extra black을 더해줌
// case 1.을 거쳐 case 2.로 온 경우 x->parent는 빨간색이었기 때문에 새로운 x는 red and black
// x는 결국 빨간색 노드가 되어 다음 while문에서 종료됨. 그리고 마지막에 x를 검정색 노드로 변경해줌
x = x->parent;
}
else
{
// Case 7. x의 형제 w가 검은색 노드이고, w의 왼쪽 자식은 검은색 노드, w의 오른쪽 자식은 빨간색 노드일 때
if (w->left->color == RBTREE_BLACK)
{
w->right->color = RBTREE_BLACK;
w->color = RBTREE_RED;
left_rotate(t, w);
w = x->parent->left;
}
// Case 8. x의 형제 w가 검은색 노드이고, w의 왼쪽 자식이 빨간색 노드일 때
w->color = x->parent->color;
x->parent->color = RBTREE_BLACK;
w->left->color = RBTREE_BLACK;
right_rotate(t, x->parent);
x = t->root;
}
}
}
x->color = RBTREE_BLACK;
}👉🏻 반복문 설정 방법
delete_fixup 함수의 while문에서 x는 항상 non-root doubly black node라고 생각하면 된다.
이 때 doubly black이란 무엇이고 왜 사용되는 것일까?
앞서 트리 재조정 과정은 검은색 노드를 삭제한 경우에만 거친다고 했다.
검은색 노드를 삭제하고 나면 트리의 black depth가 달라지므로, 삭제한 노드의 위치에 새로 자리 잡은 노드에게 임시로 추가적인 검정색을 부여하는데 이를 doubly black이라 한다.
delete_fixup 함수의 while문의 목표는 트리를 따라 extra black을 위로 옮기면서 레드 블랙 트리를 복구하는 것이라 할 수 있다.
👀 각 경우의 수
검은색 노드 삭제 후 트리를 재조정 할 때 고려하는 경우의 수는 총 여덟 가지이다.
이때 x가 부모 노드를 기준으로 왼쪽 자식인 경우와 오른쪽인 경우는 방향만 반대로 바꿔주면 되므로, 왼쪽 자식인 경우에 해당되는 네 가지 경우의 수만 살펴보자.
아래에서 x는 현재 초점을 둔 노드이고, w는 x의 형제 노드이다.
(1) x의 형제 w가 빨간색일 때
형제 노드(
w)의 색상과 부모 노드(x->parent)의 색상을 교환하고, 부모 노드를 기준으로 왼쪽으로 회전시킨다.
이 과정을 마치면 (2), (3), (4)번 케이스 중 하나에 해당하게 된다.
(2) x의 형제 w가 검은색이고, w의 자식 둘이 모두 검은색일 때
형제 노드(
w)를 빨간색으로 수정하고, 부모 노드로 초점을 옮겨 다음 반복문을 진행한다.
(3) x의 형제 w가 검은색이고, w의 왼쪽 자식이 빨간색일 때
w의 색상과w->left의 색상을 교환한 다음 오른쪽 회전시킨다.
이 과정을 마치면 (4)번 케이스가 해당하게 된다.
(4) x의 형제 w가 검은색이고, w의 오른쪽 자식이 빨간색일 때
형제노드(
w)의 색상을 부모노드의 색상(x->parent>color)으로 변경하고, 부모노드(x->parent)의 색상과w의 오른쪽 자식(w->right)의 색상을 검은색으로 변경한다. 그 다음 부모노드(x->parent)를 기준으로 왼쪽으로 회전시키고,x를root로 변경하여 while문을 종료한다.
