👀 Union-Find란?
union-find 알고리즘은 서로소 집합(disjoint-set) 알고리즘이라고도 불리는데, 두 노드가 같은 집합에 포함되는지 여부를 파악해야 할 때 사용하기 좋은 알고리즘이다.
📌 Cheat sheet (Python)
출처: 이것이 취업을 위한 코딩 테스트다 with Python
# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
# 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if parent[x] != x:
# path compression: 경로 상의 모든 노드를 루트 노드에 연결
# => 트리의 높이가 낮아지고, Find 연산의 성능이 향상됨
parent[x] = find_parent(parent, parent[x])
return parent[x]
# 두 원소가 속한 집합을 합치기 (일반적으로 값이 작은 것을 부모로 만들어줌)
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
# 노드의 개수와 간선(Union 연산)의 개수 입력 받기
v, e = map(int, input().split())
parent = [0] * (v + 1) # 부모 테이블 초기화하기
# 부모 테이블상에서, 부모를 자기 자신으로 초기화
for i in range(1, v + 1):
parent[i] = i
# Union 연산을 각각 수행
for i in range(e):
a, b = map(int, input().split())
union_parent(parent, a, b)
# 각 원소가 속한 집합 출력하기
print('각 원소가 속한 집합: ', end='')
for i in range(1, v + 1):
print(find_parent(parent, i), end=' ')
print()
# 부모 테이블 내용 출력하기
print('부모 테이블: ', end='')
for i in range(1, v + 1):
print(parent[i], end=' ')📌 Cheat Sheet (JavaScript)
function find_parent(parent, x) {
if (parent[x] !== x) {
parent[x] = find_parent(parent, parent[x]);
}
return parent[x];
}
function union_parent(parent, a, b) {
a = find_parent(parent, a);
b = find_parent(parent, b);
parent[Math.max(a, b)] = Math.min(a, b);
}
function solution(n, computers) {
const parent = Array.from({length: n}, (_, idx) => idx);
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
if (computers[i][j] === 1) {
union_parent(parent, i, j);
}
}
}
for (let i = 0; i < n; i++) {
find_parent(parent, i);
}
return new Set(parent).size;
}백준 2606번 바이러스
📝 문제
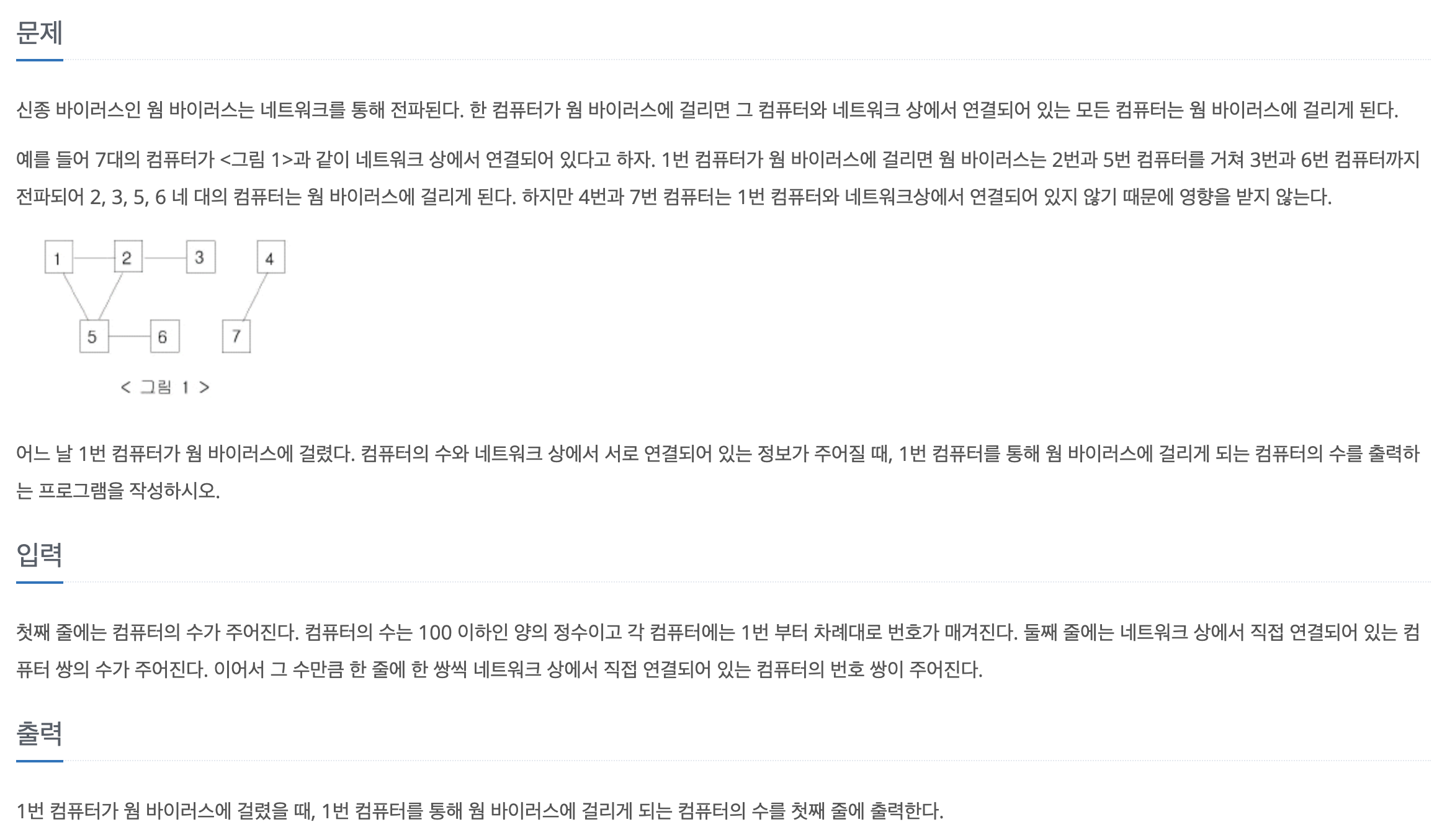
👩🏻💻 답안
import sys
def find_parent(parents, x):
if parents[x] != x:
parents[x] = find_parent(parents, parents[x])
return parents[x]
def union_parent(parents, a, b):
a = find_parent(parents, a)
b = find_parent(parents, b)
if a < b:
parents[b] = a
else:
parents[a] = b
# 컴퓨터의 수
n = int(sys.stdin.readline())
# 부모 테이블 초기화
parents = [0] * (n + 1)
for i in range(1, n + 1):
parents[i] = i
# 연결된 컴퓨터 쌍의 수
c = int(sys.stdin.readline())
# 입력값을 받고 부모 합치기 연산 수행
for _ in range(c):
a, b = map(int, sys.stdin.readline().strip().split())
union_parent(parents, a, b)
# 부모 테이블이 업데이트되지 않은 경우를 위해 각각의 노드에 대해 부모 찾기 연산 수행
for i in range(1, n + 1):
find_parent(parents, i)
# 1번 컴퓨터와 부모가 같은 컴퓨터의 개수 세기
print(parents.count(parents[1]) - 1)
백준 11724번 연결 요소의 개수
📝 문제
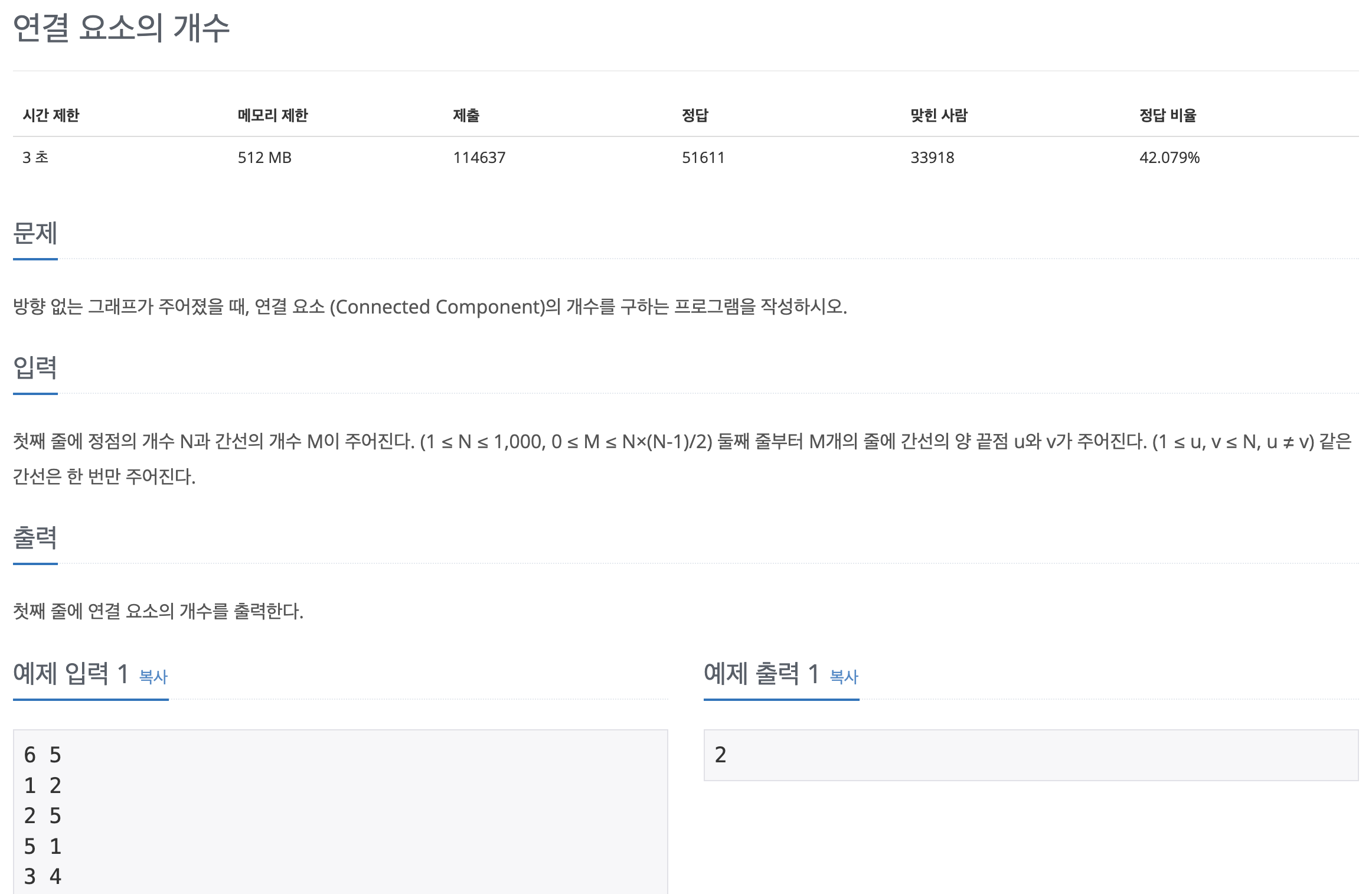
👩🏻💻 답안
import sys
def find_parent(parents, x):
if parents[x] != x:
parents[x] = find_parent(parents, parents[x])
return parents[x]
def union_parent(parents, a, b):
a = find_parent(parents, a)
b = find_parent(parents, b)
if a < b:
parents[b] = a
else:
parents[a] = b
# 정점의 개수, 간선의 개수
n, m = map(int, sys.stdin.readline().strip().split())
# 부모 배열 초기화
parents = [0] * (n + 1)
for i in range(1, n + 1):
parents[i] = i
# 간선의 양 끝점 u와 v
for _ in range(m):
u, v = map(int, sys.stdin.readline().strip().split())
union_parent(parents, u, v)
for i in range(1, n+1):
find_parent(parents, i)
parents_set = set(parents)
print(len(parents_set) - 1)백준 1197번 최소 스패닝 트리
📝 문제
💡 Spanning Tree란?
Spanning Tree는 그래프의 모든 노드를 포함하면서 사이클이 존재하지 않는 최소 연결 부분 그래프를 의미한다.
💡 최소 스패닝 트리((Minimum Spanning Tree)란?
그래프의 모든 정점들을 연결하는 부분 그래프 중에서 가중치의 합이 최소인 트리를 의미한다. 도로 네트워크에서 최소 비용으로 모든 도시를 연결하는 문제 등에 활용된다.
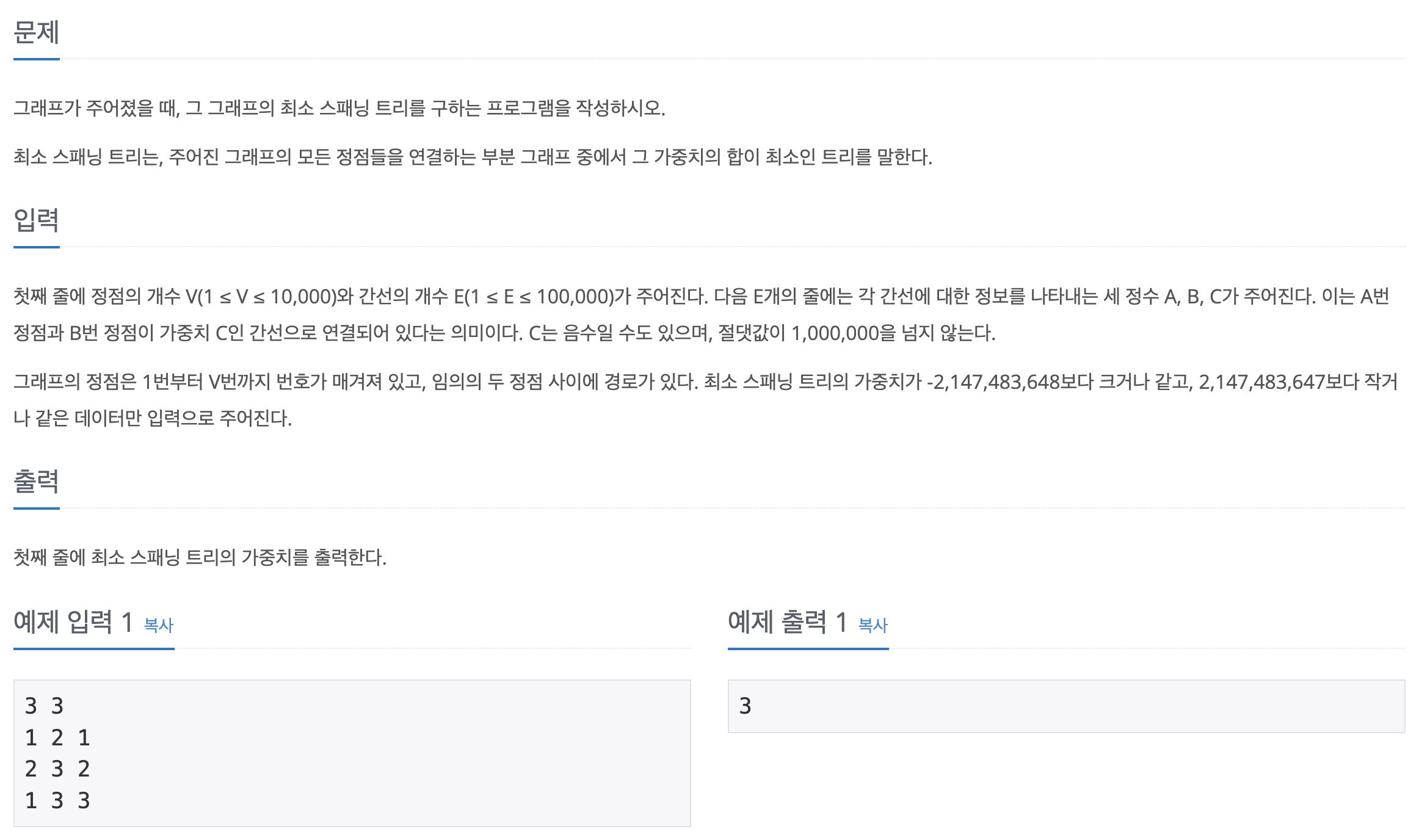
👩🏻💻 답안
최소 스패닝 트리와 관련해서 대표적인 알고리즘은 크루스칼 알고리즘(Kruskal Algorithm)인데, 아래와 같은 방법으로 구현할 수 있다.
- 그래프의 모든 간선을 가중치 순으로 정렬한다.
- 가중치가 낮은 간선부터 스패닝 트리에 추가할지 여부를 살펴본다. 👉🏻 여기에서 union-find가 사용된다.
2-1. find 연산을 했는데 부모 노드가 같다면 싸이클이 발생하는 경우이므로 스패닝 트리에 포함시키지 않는다.
2-2. find 연산 결과 부모 노드가 다르다면 union 연산을 통해 스패닝 트리에 포함한다.
import sys
# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
# 두 원소가 속한 집합을 합치기
def union_parent(parent, a, b):
a_parent = find_parent(parent, a)
b_parent = find_parent(parent, b)
# 값이 작은 것을 부모로 만들기
if a_parent > b_parent:
parent[a_parent] = b_parent
else:
parent[b_parent] = a_parent
# 노드의 개수와 간선의 개수 입력 받기
v, e = map(int, sys.stdin.readline().strip().split())
# 부모 테이블 초기화하기
parent = [0] * (v + 1)
for i in range(1, v + 1):
parent[i] = i
# 모든 간선을 담을 리스트와 최종 비용을 담을 변수
edges = []
min_cost = 0
# 모든 간선의 정보 입력 받기
for i in range(e):
a, b, cost = map(int, sys.stdin.readline().strip().split())
edges.append((cost, a, b))
# 간선을 비용순으로 정렬
edges.sort()
# 간선을 하나씩 확인하며 사이클이 발생하지 않는 경우에만 집합에 포함
for edge in edges:
cost, a, b = edge
if find_parent(parent, a) != find_parent(parent, b):
union_parent(parent, a, b)
min_cost += cost
print(min_cost)