↩️ 백트래킹
N-Queens와 같은 문제는 백트래킹으로 해결할 수 있는 대표적인 문제 중 하나이다.
백트래킹은 재귀적인 방법을 사용하여 가능한 모든 경우의 수를 탐색하는 알고리즘이다.
백트래킹은 모든 후보군에 대해 탐색을 하는데, 제약조건을 충족하지 않는 후보군의 경우 더이상 탐색을 진행하지 않고 이전 단계로 돌아가서(=backtrack) 다른 후보군의 탐색을 진행한다.
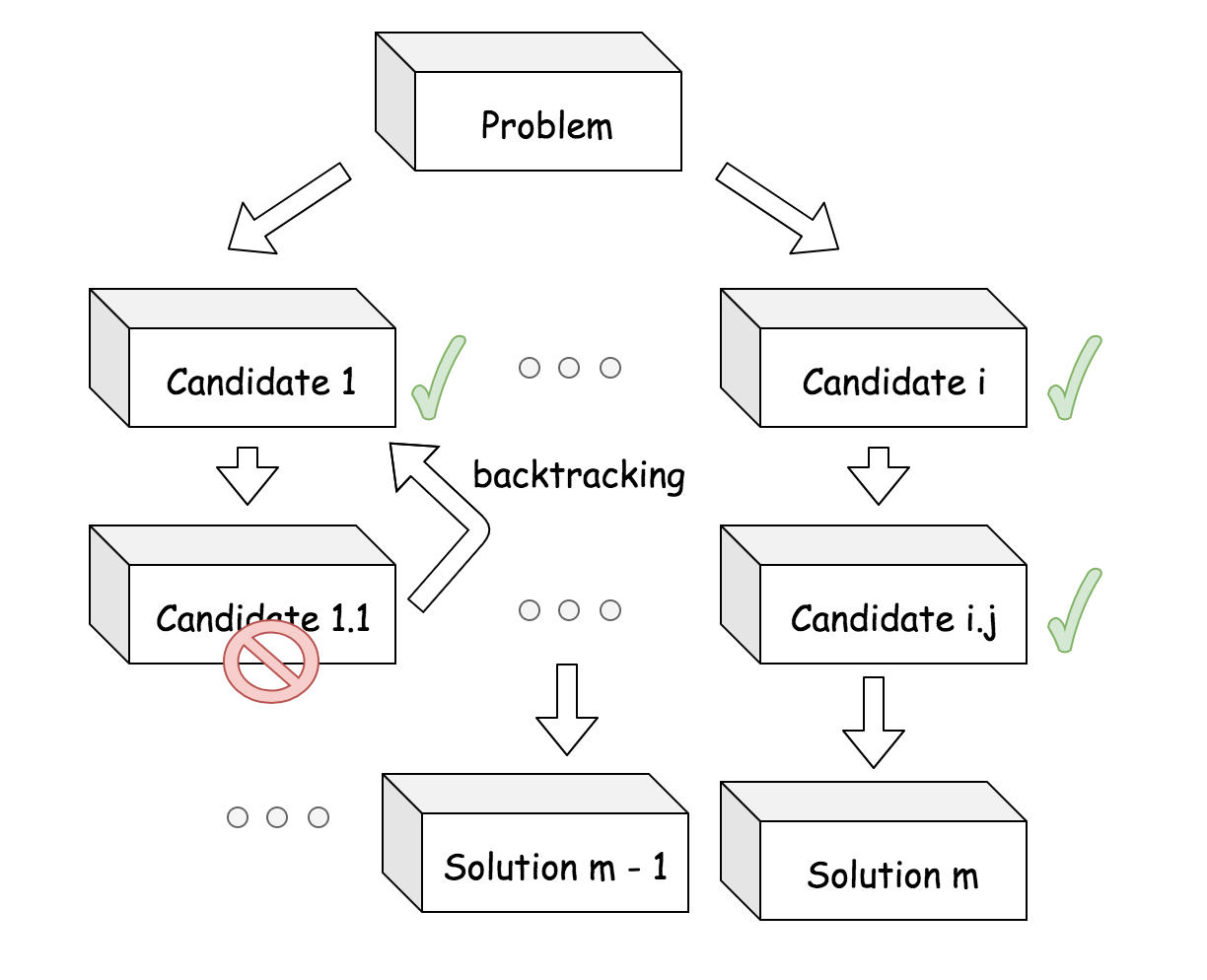
백트래킹을 트리 탐색처럼 생각하면 이해하기가 쉽다.
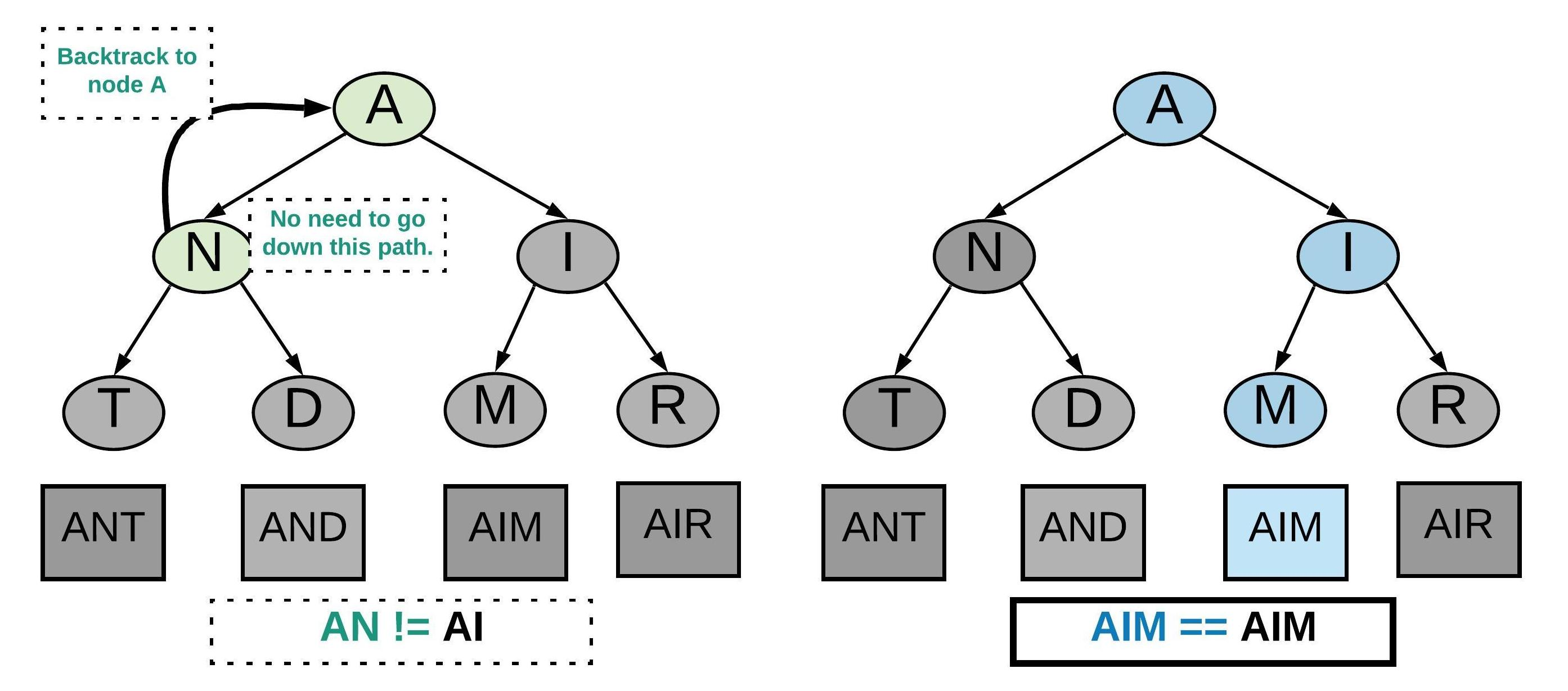
예를 들어 트리에서 "AIM"이라는 단어를 만들 수 있는 경로를 찾는 상황을 생각해보자.
브루트포스 방식으로 푼다면 단말 노드까지 내려가서 그 값이 "AIM"이 되는지 살펴볼 수 있지만 이는 비효율적이다. "A" 다음에 "N"이 오는 경우는 이미 "AIM"과 달라져서 더이상 탐색할 필요가 없기 때문이다.
백트래킹에서는 "N"과 같이 더이상 탐색할 필요가 없는 노드를 만나면 이전 단계인 "A"로 돌아가서 다음 후보군인 "I"에 대한 탐색을 시작한다.
👀 백트래킹 Cheat Sheet (Python)
백트래킹 코드는 대략 아래와 같은 포맷으로 작성할 수 있다.
def backtrack(candidate):
# 만약 현재 후보군이 유효한 해라면 정답 처리하고 backtrack 함수를 종료
if find_solution(candidate):
output(candidate)
return
# 반복문을 돌면서 가능한 모든 후보군에 대해 탐색
for next_candidate in list_of_candidates:
# 유효한 후보군인 경우에만 탐색 진행
if is_valid(next_candidate):
# 이 후보군을 우선 추가하고,
place(next_candidate)
# 후보군을 추가한 상태에서 다음 후보군에 대해서 탐색 진행
backtrack(next_candidate)
# 해당 후보군에 대한 탐색을 종료한 이후에는 제거
remove(next_candidate)📝 백준 9663번 답안
위의 내용을 참고해서 백준 9663번을 풀어보면 아래와 같이 답안을 작성할 수 있다.
import sys
sys.setrecursionlimit(10 ** 4)
"""
# Backtrack 함수의 작동 방식
(1) 현재 Row가 보드판 사이즈인 n보다 크면 가능한 방법 한 가지를 찾았다 생각하고 1을 리턴한다.
(2) 지역변수 solutions를 0으로 초기화. solutions는 현재 보드 상태에서 가능한 해결방법의 수를 나타냄
(3) 현재 Row의 모든 Columns에 대해 순회를 돌면서 퀸을 놓을 수 있는지 여부를 살펴본다.
- 현재 칸의 대각선, anti-대각선을 계산한다.
- 현재 칸의 열, 대각선, anti-대각선에 위치한 퀸이 있으면 퀸을 놓을 수 없으므로 다음 컬럼으로 넘어간다.
- 현재 칸에 퀸을 놓을 수 있다면 3개의 set(cols, diagonals, anti_diagonals)를 업데이트 하고, row+1 파라미터로 함수를 호출한다.
(4) 탐색을 완료하면 되돌아가면서(backtrack) 퀸을 회수한다. 즉, set에 추가한 값들을 제거한다.
"""
def n_queens(n):
# diagonals: 대각선으로 놓인 퀸들의 위치 정보 (row - col)
# anti_diagonals: 역방향 대각선으로 놓인 퀸들의 정보 (row + col)
# cols: 배열의 인덱스 = Row. 각 행의 몇 번째 컬럼에 퀸이 위치하는지에 대한 정보
def backtrack(row, diagonals, anti_diagonals, cols):
# Base Case: 현재 Row가 보드판 사이즈인 n이 되면 가능한 방법 한 가지를 찾았다 생각하고 1을 리턴한다.
if row == n:
return 1
# 지역변수 solutions의 값을 0으로 초기화. solutions는 현재 보드 상태에서 가능한 해결방법의 수를 나타냄
solutions = 0
for col in range(n):
# 오른쪽 아래로 내려가는 대각선은 같은 대각선에 있는 칸들의 row-col 값이 같다.
curr_diagonal = row - col
# 오른쪽 위로 올라가는 대각선은 같은 대각선에 있는 칸들의 row+col 값이 같다.
curr_anti_diagonal = row + col
# 만약 현재 칸의 열, 대각선, anti-대각선에 놓인 퀸이 있으면 퀸을 놓을 수 없으므로 다음 컬럼으로 넘어간다.
if (col in cols
or curr_diagonal in diagonals
or curr_anti_diagonal in anti_diagonals):
continue
# 현재 칸에 퀸을 놓을 수 있다면 3개의 set(cols, diagonals, anti_diagonals)를 업데이트
cols.add(col)
diagonals.add(curr_diagonal)
anti_diagonals.add(curr_anti_diagonal)
# 보드의 상태가 업데이트된 상태로 다음 행으로 넘어감
solutions += backtrack(row + 1, diagonals, anti_diagonals, cols)
# "Remove" the queen from the board since we have already
# explored all valid paths using the above function call
# 탐색을 완료하면 되돌아가면서(backtrack) 퀸을 회수한다. 즉, set에 추가한 값들을 제거한다.
cols.remove(col)
diagonals.remove(curr_diagonal)
anti_diagonals.remove(curr_anti_diagonal)
return solutions
# 처음 재귀함수를 호출하는 지점
return backtrack(0, set(), set(), set())
N = int(sys.stdin.readline())
print(n_queens(N))
📗 참고자료
LeetCode Backtraking Explore Card
Backtracking cheatsheet + simple solution
