
알고리즘 [접근 방법]
하노이 탑 문제는 재귀 함수 유형 중에 가장 대표적인 문제이다. 평소 알고리즘을 풀 때 재귀 함수 방식으로 푸는 것을 선호하지 않고 반복문으로 많이 풀다보니까 재귀 함수에 약한 느낌을 받아서 이번 글을 쓰게 되었다.
재귀 함수는 몇가지 원칙을 가지고 접근하면 쉽다.
첫번째, 탈출 조건(최소 단위)이 될 때까지 실행한다.
두번째, 일정 규칙을 찾고 구현한다.
세번쨰, 제일 큰 과정을 염두하고 구현한다.(나머지는 자동으로 됨.)
하노이 탑 문제도 마찬가지다. 하노이탑 개수와 상관없이, 일정 규칙을 찾고, 탈출 조건을 생각한다면 어렵지 않게 풀 수 있다.
일단 하노이 탑 공식부터 알아보자.
하노이 탑 이동 횟수 공식
일단, 하노이 탑의 가장 큰 규칙은 작은 원판 위에 큰 원판이 올 수 없다는 것이다.
그림을 보면서 이해해보자.
다음은 n개의 원판이 있는 하노이 탑이다.
n개의 원판을 시작 지점부터 목적 지점까지 원판을 옮기는 횟수를 구하는 함수를 Hanoi(n)이라고 하자.
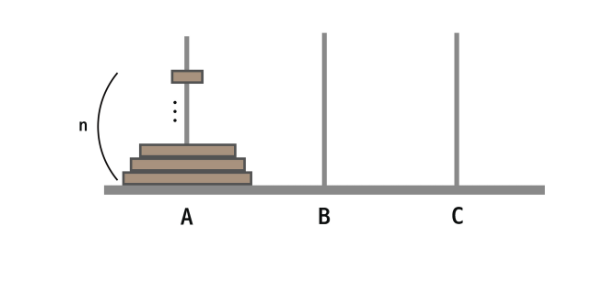
A에 있는 원판들이 최종 목적지인 C로 가기 위해서는 다음과 같은 과정들을 거치게 된다.
1. 가장 큰 원판이 C로 가려면 n-1개의 원판(나머지 원판)들이 A에서 B로 가야한다.
결국 가장 큰 원판이 C 맨 아래에 깔려야하므로 n-1개의 원판이 모두 B로 옮겨져야한다.
즉, n-1개의 원판이 A가 시작지점 B가 목적 지점이 된 Hanoi(n-1)이 이 시점까지의 이동 횟수가 된다.
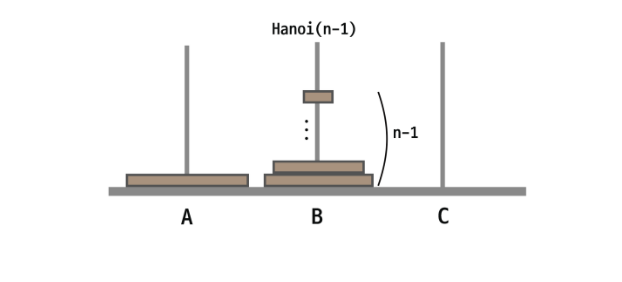
2. 그리고 A에 있는 가장 큰 원판이 C로 이동해야한다.
이 이동은 가장 큰 원판만 이동하기 때문에 횟수는 1회이다.
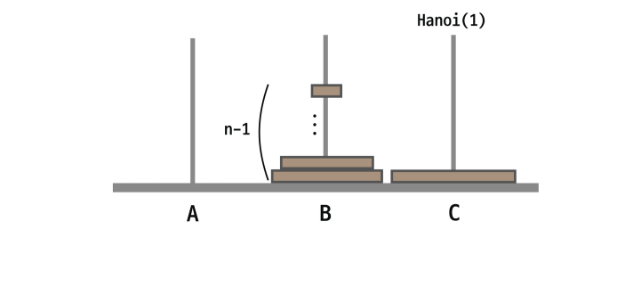
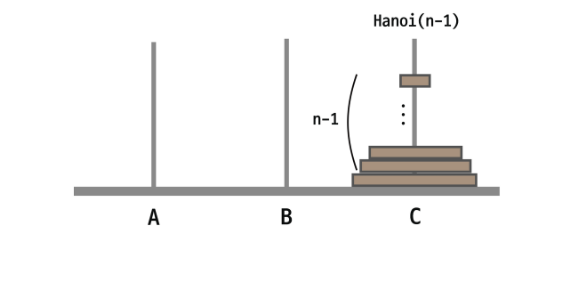
3. B에 있는 n-1개의 원판을 C로 이동한다.
앞서 1번 과정에서 A -> B로 n-1개가 이동했듯이, B -> C로 n-1개가 움직이는 과정을 거쳐야한다.
즉, Hanoi(n-1)가 이 시점에서의 이동 횟수가 된다.
수열로 표현
앞선 1, 2, 3번을 거치면 Hanoi(n)을 수열로 표현할 수 있게된다.
Hanoi(n) = 2 × Hanoi(n-1) + 1
이를 점화식으로 표현하면 다음과 같다.(velog에서 수식 표현 지원이 안되어서 다음과 같이 표현함.)
a[1] = 1 , a[n+1] = 2 * a[n] + 1
이를 귀납적으로 정리해보자.
1. 위의 점화식의 양변에 1을 더해 우변을 다음과 같이 묶어준다.
a[n+1] + 1 = 2(a[n] + 1)
2. a[n+1] + 1을 b[n]이라고 정의
b[n] = a[n] + 1
3. a[n+1] -> b[n] 대입
b[n] = 2*b[n]
-> 점화식 완성
4. 첫째항으로 밑 구하기
b[1] = a[1] + 1 = 2
5. 마무리
첫째항은 2이고 공비는 2인 공비수열이 된다.
=> b[n] = a[n] + 1 = 2^n(2의 n제곱 이라는 뜻)
=> a[n] = 2^n - 1
이 공식이 원판 이동 횟수이다.
이제 재귀 함수를 이용해 경로를 출력하는 알고리즘을 짜보자.
하노이 탑 재귀 알고리즘
앞선 규칙을 알아내는 과정을 다시 정리해보자.
A -> C로 n개의 원판을 옮기려면
1. A -> B로 n-1개의 원판을 옮기고,
2. A -> C로 가장 큰 원판을 옮기고,
3. B -> C로 n-1개의 원판을 옮겨야한다.
시작 지점을 start, 목적 지점을 to, 중간에 있는 막대기를 mid라고 표현을 한다.
그리고 A 막대기는 1, B 막대기는 2, C 막대기는 3이라고 표현한다.
이를 코드로 표현해보자.
// 1 -> 3으로 n개를 옮김.
public static void hanoi(int n, int start, int mid, int to) {
// 이동할 원판의 수가 1개일 때(탈출 조건)
if (n == 1) {
sb.append(start + " " + to + "\n");
return;
}
// 1 -> 2로 n-1개를 옮김.
// 위의 1번 과정
hanoi(n - 1, start, to, mid);
// 가장 큰 원판을 목적 지점으로 옮김
// 위의 2번 과정
sb.append(start + " " + to + "\n");
// 2 -> 3으로 n-1개를 옮김.
// 위의 3번 과정
hanoi(n - 1, mid, start, to);
}나는 위의 코드가 한번에 와닿지가 않아 노트에 직접 그려가며 재귀 함수를 돌려보았다. 그 와중에 규칙에서 어디 부분에 이 코드가 해당하는지 확인하면 이해 하는데에 큰 도움이 될 것이다.