문제 : https://www.acmicpc.net/problem/2342

출처 : https://www.acmicpc.net/problem/2342

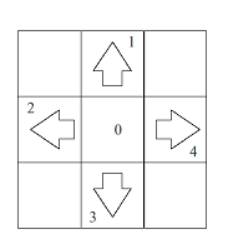
게임장에 가면 흔히 있는 DDR이다. 가운데에 왼발, 오른발을 두고 시작한다. 문제 규칙은 다음과 같다.
1. 해당위치를 밟으면 1
2. 인접한 위치를 밟으면 3
3. 반대방향 밟으면 4
예를 들어, 왼쪽 발이 2의 위치에 있고 4의 위치로 간다면 힘이 4가 들고, 0,1,3의 위치로 간다면 3, 제자리인 2의 위치로 간다면 1의 힘이 드는 것이다.
이를 이용하여 드는 힘의 최소비용을 구하면 된다.

풀이

해당 문제를 풀기 위해서 dfs + dp를 알아야 된다. 필자가 적었던 저번 글을 보면 dfs는 특정 조건을 걸어주지 않으면 전체탐색을 할 때 같은 연산을 또 하게 된다. 따라서 이미 했던 연산이라면 바로 return하는 것이 중요하다. 또한 해당 문제에서 중요한 점은 dp 아이디어이다. 필자 같은 경우 dp를 삼차원 배열로 다음과 같이 선언하였다.
n = commands의 길이, left = 5, right = 5 -> nx5x5의 크기를 지닌 3차원 행렬

예를 들어, 첫번째의 커맨드가 1이라면 dp는 두가지의 경우를 생각할 수 있다.
dp[1][1][0] = 첫번째 커맨드에 대해서 왼쪽 발이 움직인 경우
dp[1][0][1] = 첫번째 커맨드에 대해서 오른쪽 발이 움직인 경우

또 다른 예시로, 마지막 커맨드가 3이라면 dp는 두가지의 경우를 생각할 수 있다.
dp[n-1][1][0] = 마지막번째 커맨드에 대해서 왼쪽 발이 움직인 경우
dp[n-1][0][1] = 마지막번째 커맨드에 대해서 오른쪽 발이 움직인 경우

거꾸로 생각해서 마지막부터 시작하면 n-1번째 사용된 힘은 0이다. n-2번째 사용된 힘은 n-1번째로부터 움직여서 사용된 힘을 저장한다. n-3번째 사용된 힘은 n-2번째까지 사용된 힘과 n-3번째 사용된 힘의 sum이다. dp는 위처럼 탐색하면서 min값으로 저장된다. 따라서 dp[0][0][0]에는 모든 경우를 탐색하고 최종 min sum값을 저장한다.

또한 필자는 딕셔너리를 사용하여 사용되는 힘을 아래와 같이 간단하게 저장하였다.

rules = {0:[1,2,2,2,2], 
         1:[2,1,3,4,3],
         2:[2,3,1,3,4],
         3:[2,4,3,1,3],
         4:[2,3,4,3,1],
        }

code

import sys
sys.setrecursionlimit(99999)
rules = {0:[1,2,2,2,2], 
         1:[2,1,3,4,3],
         2:[2,3,1,3,4],
         3:[2,4,3,1,3],
         4:[2,3,4,3,1],
        }

start = (0,0,0)
commands = list(map(int,input().split()))
commands = [0] + commands[:-1]
n = len(commands)
dp = [[[-1]*5 for _ in range(5)] for _ in range(n)]

def dfs(cur):
    index, left, right = cur
    if index==n-1:
        return 0
    if not (left==0 and right==0) and left==right:
        return 99999999
    if dp[index][left][right]!=-1:
        return dp[index][left][right]
    
    dp[index][left][right]=min(dfs((index+1,left,commands[index+1])) + rules[right][commands[index+1]],
                              dfs((index+1,commands[index+1],right)) + rules[left][commands[index+1]])
    return dp[index][left][right]
print(dfs((0,0,0)))

Result