문제 : https://www.acmicpc.net/problem/7578

문제

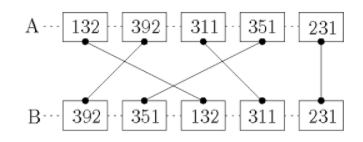
A와 B에는 고유 번호들이 있고, 각 번호끼리 잇는 직선들 중에 교차점을 세는 문제이다.
문제 해석은 쉬우므로 자세한 설명은 생략한다.

풀이

주어진 입력 조건을 통해 새로 index를 저장하자

문제에서 n을 입력받고 A,B 순서대로 입력받는다. 여기서 A와 B의 고유번호가 동일하다는 점을 이용하여 dictionary를 만든다.

n = int(input())
A = list(map(int,input().split()))
B = list(map(int,input().split()))
machines = {}
for i,b in enumerate(B):
    machines[b] = i

위와 같이 machines 딕셔너리를 사용하여 순서대로 A를 읽을 때 각 number를 키 값으로 value를 얻는다면 시간복잡도는 1이 된다(java에서 hashmap같은 개념)

선형탐색 사용?

교차점 개수를 셀 때 해당 지점으로부터 얼마나 교차를 했는지 탐색을 한다면 최악의 경우 N^2를 갖게 될 것이다. 따라서 선형탐색이 아닌 교차점을 셀 수 있는 다른 방법을 생각해봐야된다.

세그먼트 트리

주어진 배열에 따라 binary tree를 만들어주고 각 노드에 구간합을 갱신하며 트리를 만든다면, 갱신할 때마다 높이(logn)만큼 걸리고, query를 구할 때도 높이(logn)밖에 걸리지 않는다. 이를 이용하면 교차점 개수를 갱신할 때마다 시간이 덜 걸릴 것이다.

구현

참고 : https://www.crocus.co.kr/648

우선 initialize 부터 해보자.
세그먼트 트리의 높이가 logn임을 이용하여 배열을 만들면 다음과 같이 만들 수 있다.

height = math.ceil(math.log2(n))
tree = [0] * (1<<(height+1))

binary tree array의 경우 부모노드(i)는 왼쪽 자식노드(i2)와 오른쪽 자식노드(i2+1)를 가지고 있다. 즉 인덱스 번호를 통해 접근을 할 수 있다. 이를 이용하여 update를 구현하면 다음과 같다.

def update(node, start, end, idx):
    if idx<start or idx>end: # 해당 범위 바깥
        return 0
    if start == end:
        tree[node] = 1
        return 1
    mid = (start + end)//2
    update(node*2, start,mid, idx)
    update(node*2+1, mid+1,end,idx)
    tree[node] = tree[node*2] + tree[node*2+1]
    return tree[node]

첫번째 if문은 tree 범위 안에 없으므로 return 0을 해준다.
두번째 if문은 가장 리프노드에 해당하는 부분이므로 1를 대입해준다.
만약 두번째 if문까지 걸러지지 않았다면 이는 중간 높이에 해당하는 노드이므로 왼쪽 노드와 오른쪽 노드의 값을 더해줘야된다.

tree[node] = tree[node*2] + tree[node*2+1]

그리고 구간합을 하기전 리프노드들을 모두 갱신해줘야 하므로 재귀적으로 update함수를 호출한다. 이때 인자값은 좌측노드와 우측노드의 인덱스 값으로 넣어준다.

update(node*2, start,mid, idx)
update(node*2+1, mid+1,end,idx)

이때 start와 end의 범위가 줄어든 것도 노드마다 구간이 달리지기 때문에 변경해줘야된다(이진 탐색처럼).

그럼 이제 query를 구현해보자.
update함수와 같이 이진탐색 방식으로 접근한다. 그리고 index가 해당 구간내에 존재할 때 해당 노드값을 읽어오면 된다.

def query(node, start, end, left, right):
    if right<start or left>end:
        return 0
    if left<=start and right>=end:
        return tree[node]
    mid = (start+end)//2
    return query(node*2, start,mid, left, right) + query(node*2+1, mid+1, end, left, right)

여기서 구간은 해당 지점으로부터 마지막까지로 설정되어 있는데 이는 문제조건에 맞게 해당 지점으로부터 트리에 끝부분까지만 구해주면 되기 때문이다.

result

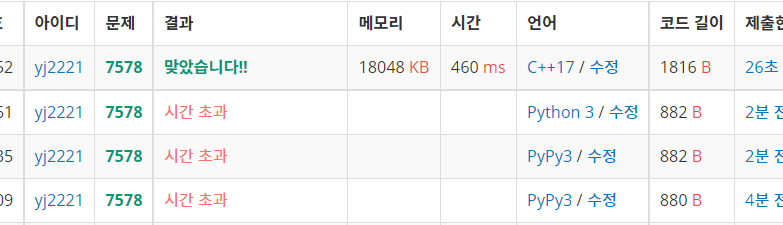
python으로 할때 시간초과라고 계속 떳다. 그래서 C++ 버전으로 코드를 바꿔서 실행해본 결과 맞았다고 떳다. 이래서 삼성sw아카데미에서 C++를 추구하나보다...
추가 : 다른 사람의 python 코드를 본 결과 비트연산을 되도록 많이 사용하였다. 아마 비트연산이 빠르기 때문에 그런거 같다.