백준 내접사각형 만들기

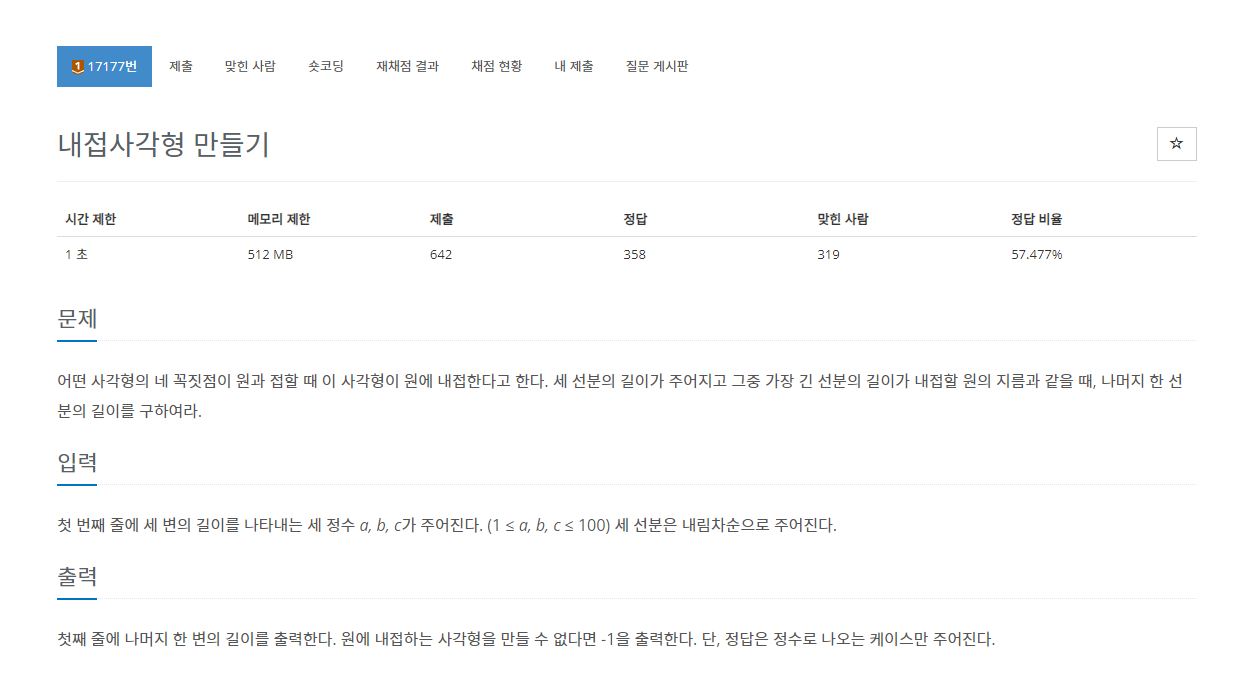
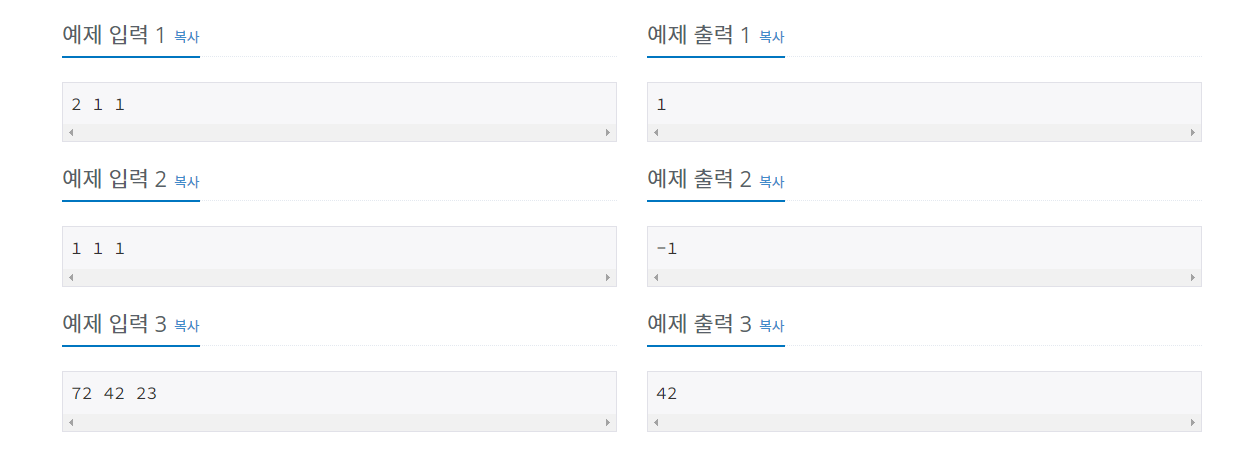
문제

내가 생각했을때 문제에서 원하는부분

첫 번째 줄에 세 변의 길이를 나타내는 세 정수 a, b, c가 주어진다.
(1 ≤ a, b, c ≤ 100) 세 선분은 내림차순으로 주어진다.
첫째 줄에 나머지 한 변의 길이를 출력한다. 원에 내접하는 사각형을 만들 수 없다면 -1을 출력한다.
단, 정답은 정수로 나오는 케이스만 주어진다.

내가 이 문제를 보고 생각해본 부분

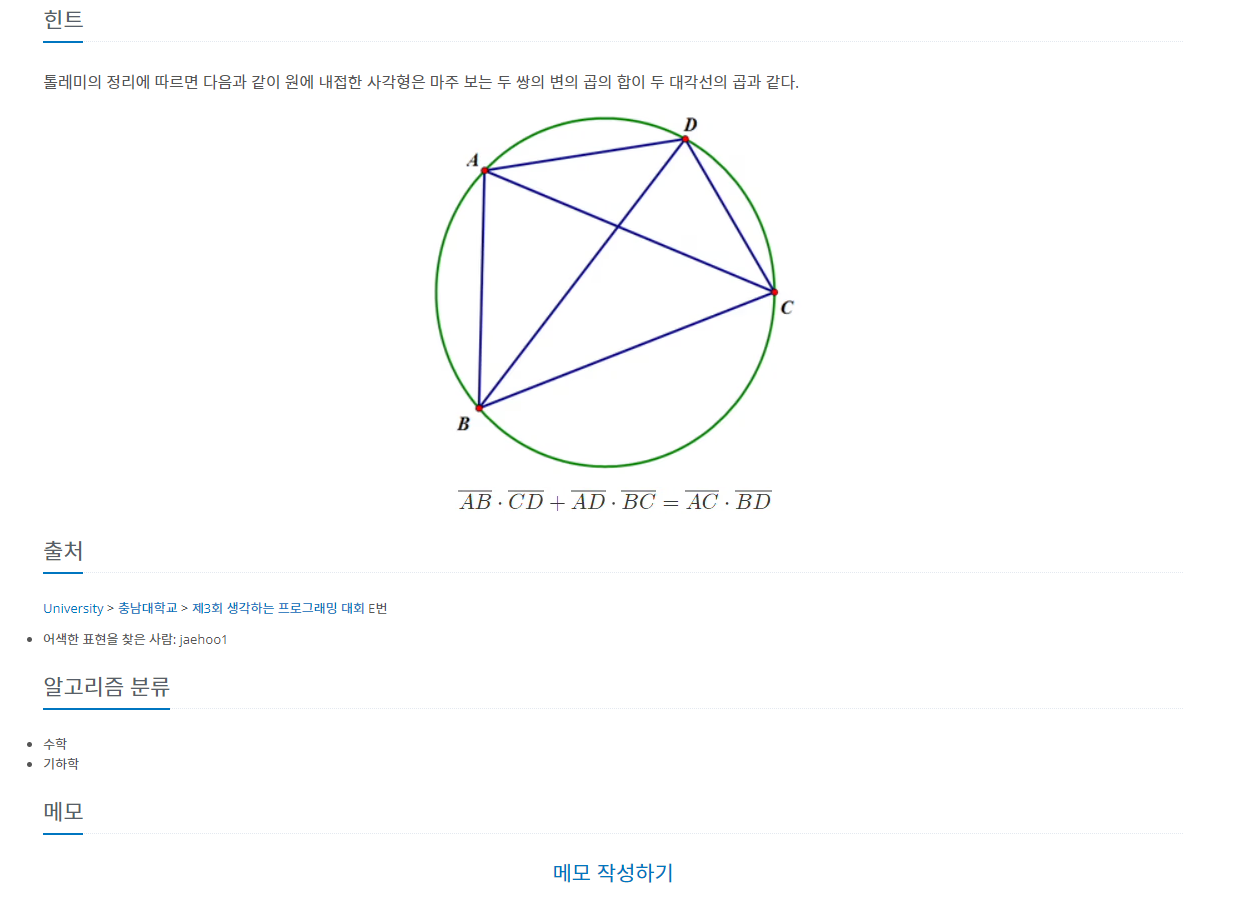
일딴 나는 먼저 톨레미의 정리의 역이 설립하는지 생각해봤다.
디행히 톨레미의 정리는 역도 성립한다.

새로운 변의 길이를 x라 하면, 두 대각선의 길이는 피타고라스 정리에 의해 구할 수 있으며, 방정식을 풀어 x를 찾으면 된다.

코드로 구현

package baekjoon.baekjoon_19;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

// 백준 17177번 문제
public class Main659 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        String[] input = br.readLine().split(" ");
        int a = Integer.parseInt(input[0]);
        int b = Integer.parseInt(input[1]);
        int c = Integer.parseInt(input[2]);

        int p = a;
        int q = 2 * b * c;
        int r = a * (c*c - a*a + b*b);

        int d = q*q - 4*p*r;
        if(d < 0) {
            System.out.println(-1);
            return;
        }

        double x = (-q + Math.sqrt(d)) / (2*p);

        if(x < 0) {
            System.out.println(-1);
            return;
        }

        System.out.println((int)(x + 1e-5));
        br.close();
    }
}

마무리

오늘 문제가 많이 어렵게 느껴졌다. 특히 톨레미의 정리를 몰랐었는데 이 문제를 계기로 톨레미의 정리를 알게됐다.