[Algorithm] 02. Huffman Coding

Huffman Encoding이란?

• Greedy algorithm의 대표적인 예시
  *Greedy Algorithm: 매 순간 가장 이득이 되는 선택을 하는 알고리즘

• 문자들의 '빈도수'를 기반으로, 자주 나오는 문자는 짧은 코드, 길게 나오는 문자는 긴 코드를 부과하여 전체 메시지의 길이를 최소화
  -> 총 비트수를 줄일 수 있음

• Prefix code: 어떤 문자 코드도 다른 문자의 접두어가 되게 하지 않는 것 ex. 101, 1010이 동시에 존재 불가

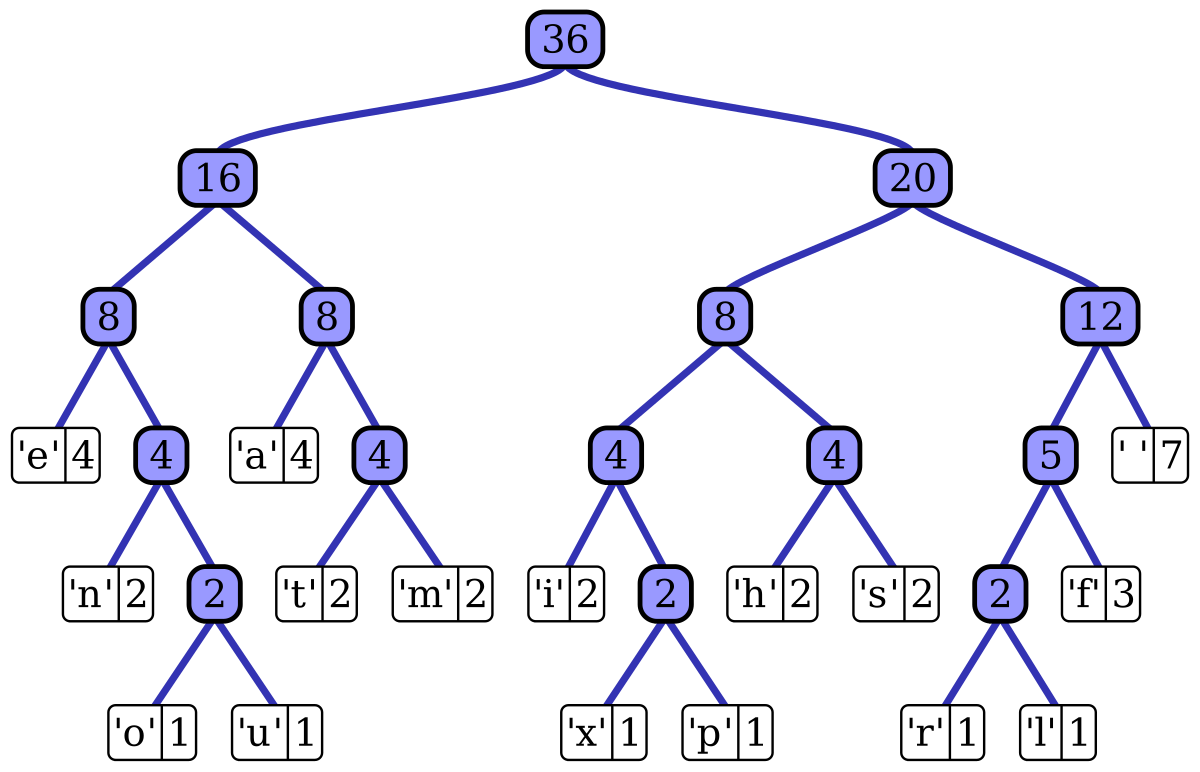
• Huffman Tree 구조
  : 제일 자주 나오는 문자일수록 루트에 더 가까이 위치
  

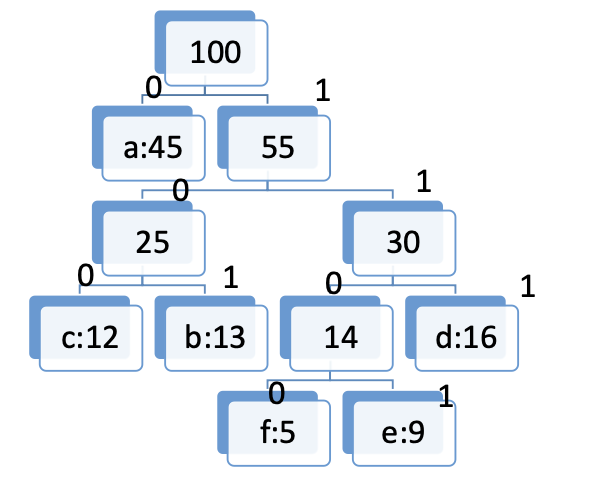
Huffman Algorithm

기본 작동 원리

1. 모든 문자를 리프 노드로 만들고, 빈도 기준으로 min heap에 넣음
2. 가장 작은 빈도 2개 꺼냄
3. 두 노드를 합쳐서 두 노드의 합인 새로운 노드 생성 후 힙에 넣음
4. 다시 제일 작은 빈도의 2개를 꺼냄
5. 이 과정을 노드가 2-3개 남을 때까지 반복

• Create min heap
  

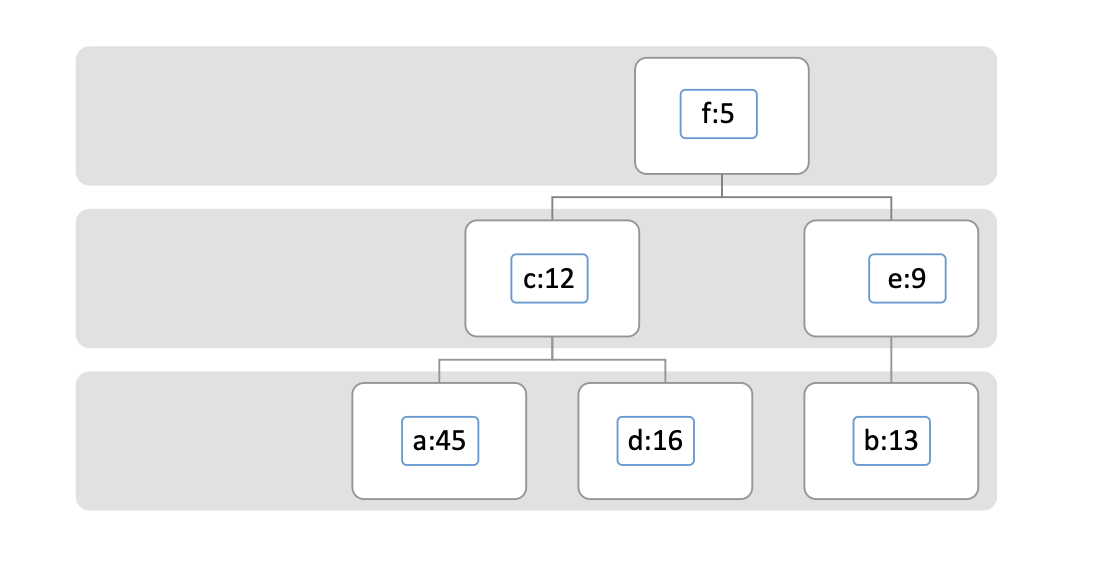
• Extract the smallest two
  
  
  
  

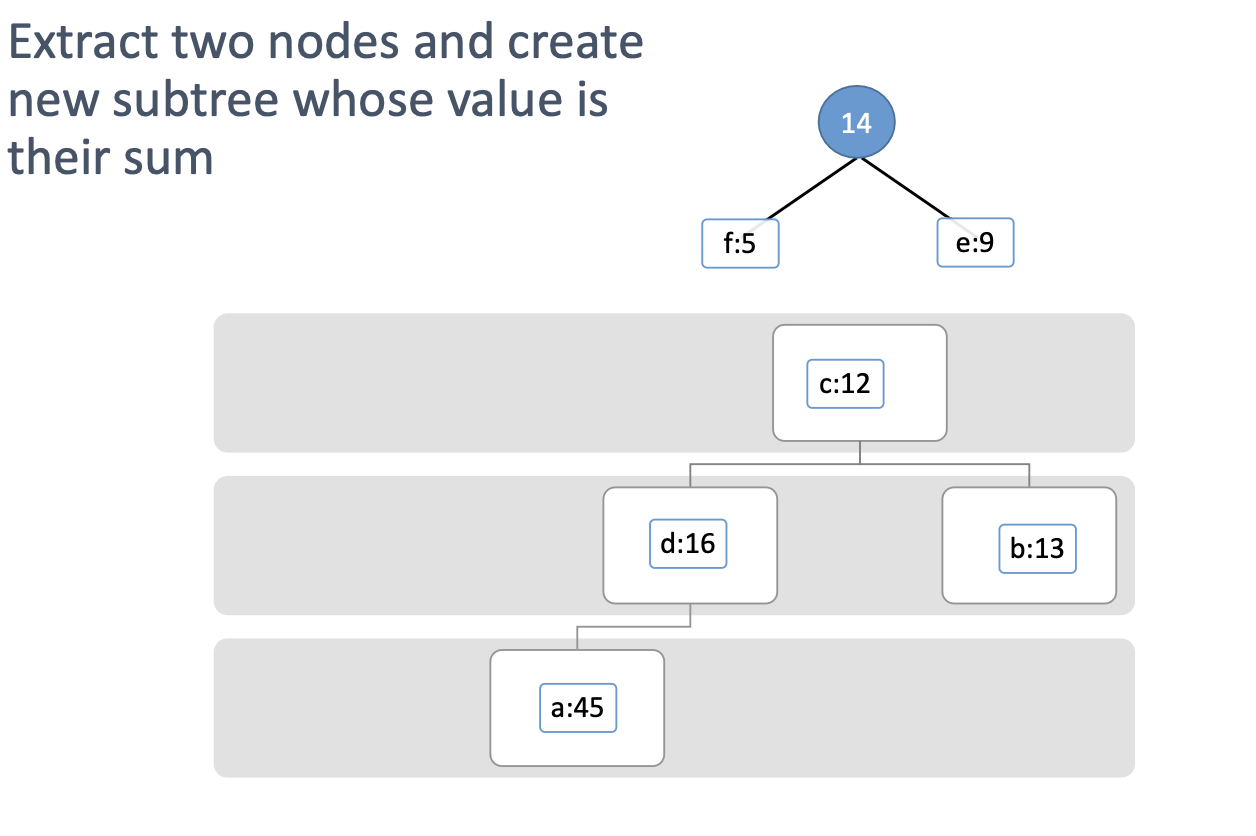
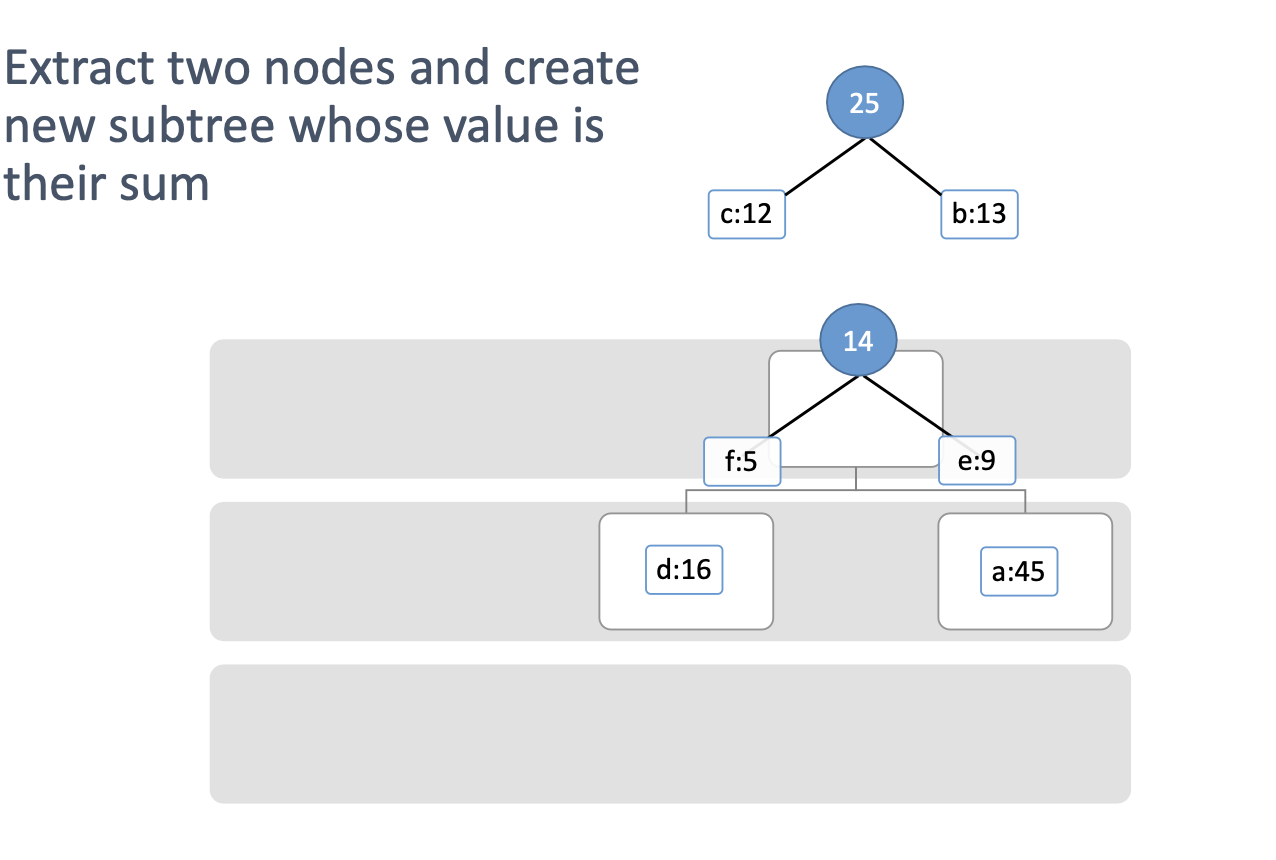
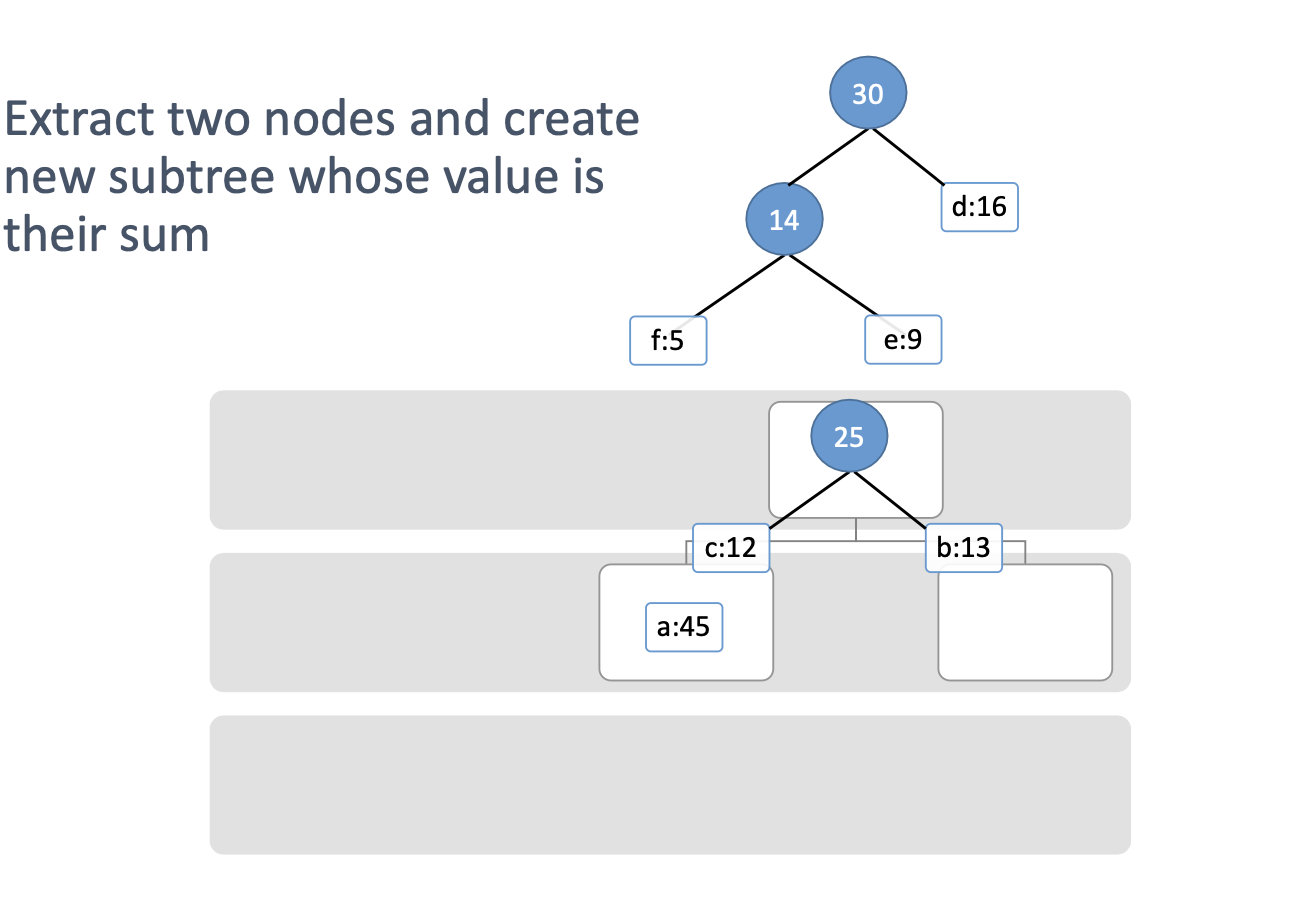
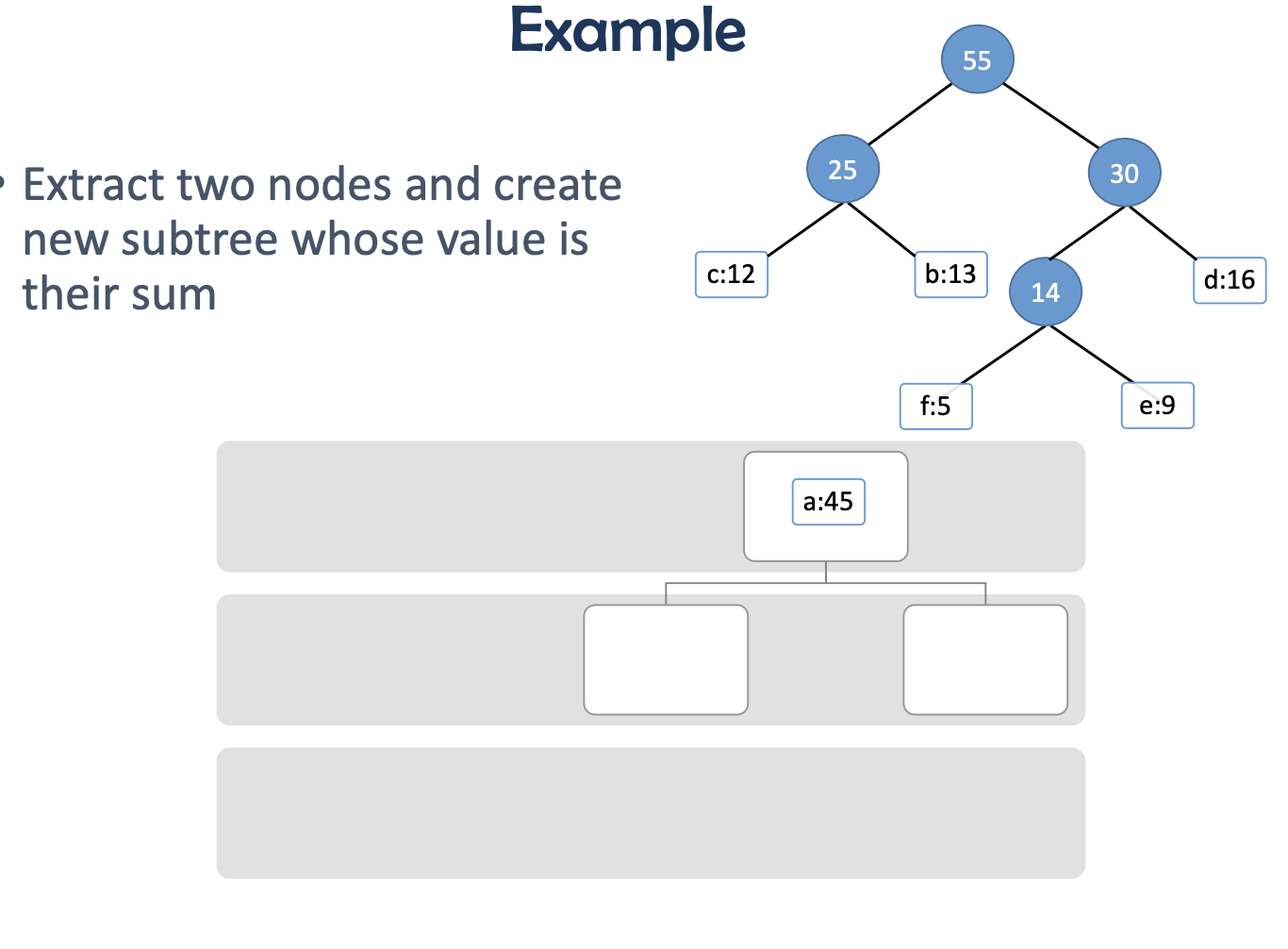
-> 위의 이미지들은 새로운 노드 생성 후 다시 최소 힙에 넣는 작업은 생략함. 실제 알고리즘 구현에서는 꼭 다시 최소 힙에 넣어야함

• 시간복잡도: O(nlogn)

Java를 이용한 구현

import java.util.PriorityQueue;
import java.util.Comparator;

public class Huffman {
    // Huffman 트리의 루트 노드
    private HuffmanNode root = null;

    // HuffmanNode 클래스: 트리의 노드 하나를 나타냄
    class HuffmanNode {
        int data; // 빈도수
        char c; // 문자
        HuffmanNode left;  // 왼쪽 자식
        HuffmanNode right; // 오른쪽 자식
    }

    // 우선순위 큐에서 사용할 Comparator 정의 
    class MyComparator implements Comparator<HuffmanNode> {
        public int compare(HuffmanNode x, HuffmanNode y) {
            return x.data - y.data; //빈도수 기준 오름차순 정렬
        }
    }

    // 생성자: 문자 배열과 빈도 배열을 입력받아 Huffman 트리를 생성
    public Huffman(char[] charArray, int[] charfreq) {
        int n = charArray.length;

        // 우선순위 큐 생성 (최소 힙)
        PriorityQueue<HuffmanNode> q = new PriorityQueue<>(n, new MyComparator());

        // 1. 각 문자에 대해 리프 노드를 생성하여 큐에 추가
        for (int i = 0; i < n; i++) {
            HuffmanNode hn = new HuffmanNode();
            hn.c = charArray[i];
            hn.data = charfreq[i];
            hn.left = null;
            hn.right = null;
            q.add(hn);
        }

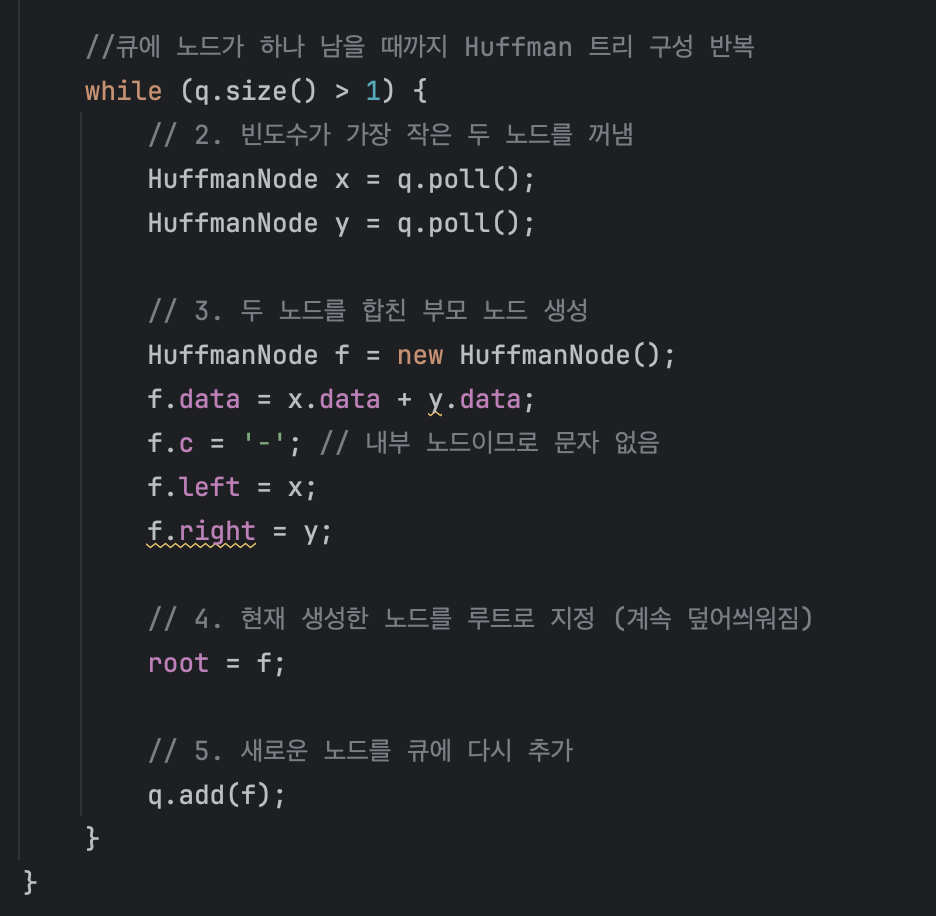
        //큐에 노드가 하나 남을 때까지 Huffman 트리 구성 반복
        while (q.size() > 1) {
            // 2. 빈도수가 가장 작은 두 노드를 꺼냄
            HuffmanNode x = q.poll();
            HuffmanNode y = q.poll();

            // 3. 두 노드를 합친 부모 노드 생성
            HuffmanNode f = new HuffmanNode();
            f.data = x.data + y.data;
            f.c = '-'; // 내부 노드이므로 문자 없음
            f.left = x;
            f.right = y;

            // 4. 현재 생성한 노드를 루트로 지정 (계속 덮어씌워짐)
            root = f;

            // 5. 새로운 노드를 큐에 다시 추가
            q.add(f);
        }
    }

    // Huffman 코드 출력 (외부에서 호출할 수 있는 wrapper 함수)
    public void printCode() {
        printCode(root, "");
    }

    // 재귀적으로 트리를 순회하며 각 문자의 Huffman 코드를 출력
    public void printCode(HuffmanNode root, String s) {
        // 리프 노드에 도달하면 코드 출력
        if (root.left == null && root.right == null && Character.isLetter(root.c)) {
            System.out.println(root.c + " : " + s);
            return;
        }

        // 왼쪽으로 가면 0, 오른쪽으로 가면 1 추가
        printCode(root.left, s + "0");
        printCode(root.right, s + "1");
    }
}

• 주요 알고리즘은 다음과 같음

1. Huffman tree 생성 및 min heap 생성하여 리프 노드를 해당 힙에 추가
   

2. Queue에 노드가 하나 남을 때까지 트리 구성 반복