[Algorithm] 09. Divide and Conquer

주영진·2025년 5월 14일

Algorithm 스터디

목록 보기

7/8

1. 분할정복(Divide and Conquer)이란?

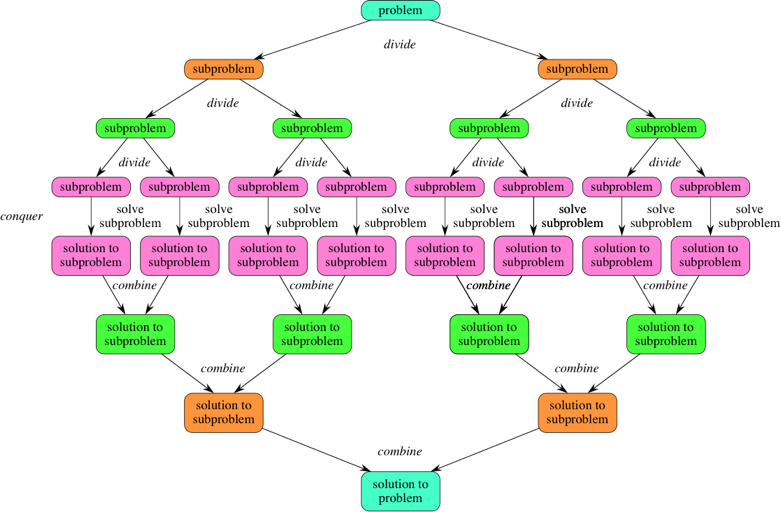
'큰 문제'를 '작은 문제'로 나누어서 해결하는 알고리즘

조금 더 풀어 말하자면, 하나의 큰 문제를 작은 부분의 문제들로 나누고, 나눈 부분 문제를 해결하고 해결된 해들을 모아 원래의 문제를 해결해 나가는 방식이다. 따라서 크게 '분할 > 정복 > 결합'의 단계를 지닌다.

분할(Divide): 첫번째로 문제를 ‘작은 부분 문제들로 나눈다.
정복(Conquer): 두번째로 각각의 ‘부분 문제’를 해결한다.
결합(Combine): 세번째로 ‘부분 문제’들의 해를 모아서 원래 문제의 해를 구한다.

2. 재귀를 이용한 분할정복

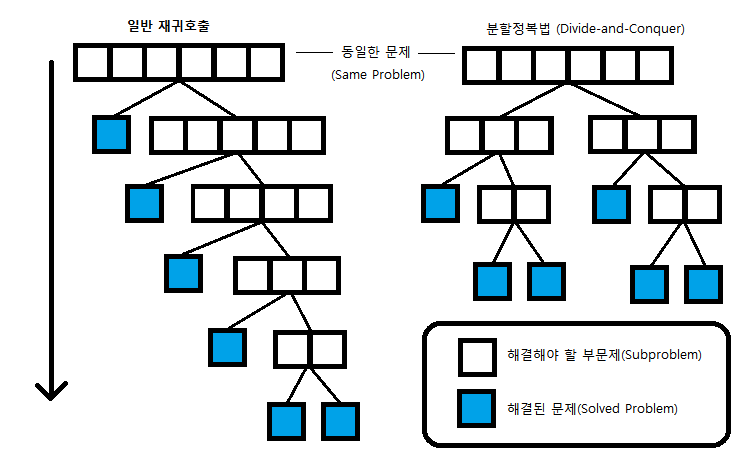
'재귀'를 활용하여 작은 부분으로 나누어 문제를 해결하지만, 일반적인 재귀와는 차이가 있다

분할정복은 작은 부분으로 문제를 해결해나가는 과정에서 재귀를 활용하지만, 일반적인 재귀와는 달리 전체의 과정이 분할 후 해결해나가는 과정과, 결합해서 해결해나가는 과정으로 분리되어 있다는 점에서 차이가 존재한다. 또한, 일반적인 재귀가 가지는 대규모 문제를 해결 시 생기는 호출 스택의 문제를 해결하기에도 분할정복이 더 용이하다는 장점이 있다. 또한, 부분 문제들이 독립적이므로 병렬 처리가 가능하다.

분할정복의 시간 복잡도는 일반적으로 O(nlogn)을 가진다.

3. 구현 방법

1. Quick sort

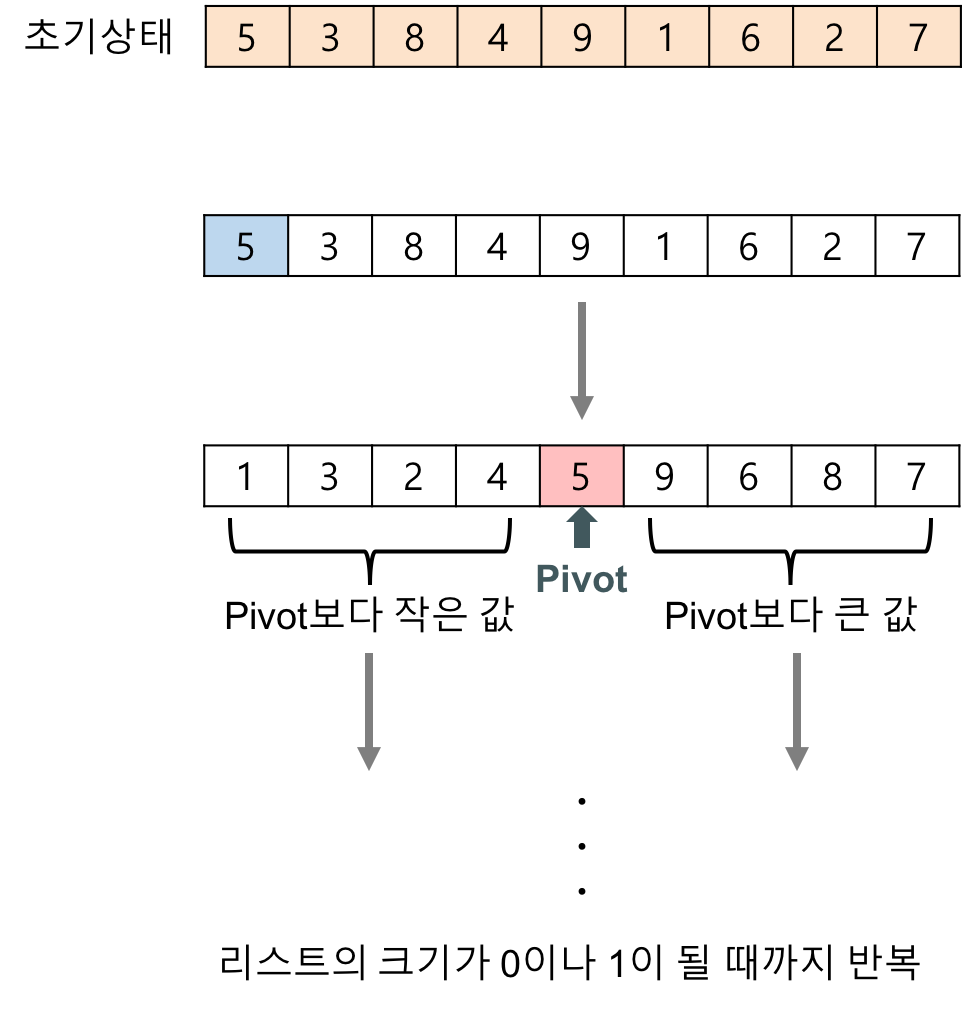
퀵 정렬을 수행해가는 과정은 다음과 같다.

배열에서 pivot을 선택한다. 이때 pivot은 배열의 중간값, 첫 번째 값, 마지막 값 등 여러 기준으로 선택될 수 있다.
pivot을 기준으로 두 개의 서브 배열로 분할해, Piovt보다 작은 값을 왼쪽 서브 배열에, 큰 값은 오른쪽 서브 배열에 위치시킨다.
각 서브 배열을 quick sort한다.
정렬된 서브 배열을 결합한다.

public static void quickSort(int[] arr, int left, int right) {
    if (left >= right) return;

    int pivot = partition(arr, left, right);

    quickSort(arr, left, pivot - 1);
    quickSort(arr, pivot + 1, right);
}

/**
 * 분할 적용 : 주어진 구간에서 피봇을 선택하고, 분할을 수행하는 함수
 */
public static int partition(int[] arr, int left, int right) {
    int pivot = arr[left];
    int i = left + 1;
    int j = right;

    while (i <= j) {
        while (i <= right && arr[i] < pivot) i++;
        while (j >= left + 1 && arr[j] > pivot) j--;

        if (i > j) {
            swap(arr, left, j);
        } else {
            swap(arr, i, j);
        }
    }
    return j;
}

/**
 * 값 변경 : 배열에서 두 원소의 위치를 바꾸는 함수
 */
public static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}