[TIL] 20210805 - 자료구와 알고리즘2

intro

오늘로 데브코스 4일차를 맞이했다.

강의수강, 실습 과제, CS스터디 과제, TIL작성, 아티클작성 등... 해야할 것들이 많은데 아직 초반이라 우왕좌왕한 것 같다.🤪

처음에는 하루에 해야할 태스크 하나하나에 많은 시간이 소모가 되었는데 점점 태스크의 노하우가 쌓이는것이 느껴진다.

특히 TIL 작성 경험이 부족하다보니 나만의 틀이 없었고 딱딱한 학습 메모장같은 느낌이 들었다. 🥲

다른 분들이 작성한 훌륭한 TIL을 보면서 감탄을 금치 못했는데 덕분에 어떤식으로 TIL을 작성해야할지 감을 잡고 있다. (나... 잘 하고있는거겠지??)

오늘 학습한 내용

자료구조와 알고리즘 내용들을 학습하면서 실습을 통해 적용해보는 시간을 가졌다.

1. 트리
2. 힙
3. 트라이
4. 정렬
5. 이진탐색
6. BFS, DFS
7. 그리디
8. 코테 준비 방법

자료구조와 알고리즘 후반부 파트이며 내 기준에는 어렵기도 하지만 중요한 내용들이라고 생각한다.

트리

트리란?

방향 그래프의 일종, 정점을 가리키는 간선이 하나 밖에 없는 구조

루트, 자식노드, 레벨이 존재한다.

트리특징

• 루트 정점을 제외한 모든 정점은 반드시 하나의 부모 정점을 갖는다.
• 정점이 N개인 트리는 반드시 N-1개의 간선을 갖는다.
• 루트에서 정점으로 가는 경로는 유일하다.

이진 트리

• 각 정점이 최대 2개의 자식을 가지는 트리

• 이진 트리, 완전 이진 트리, 포화 이진 트리, 평향 이진 트리로 분류된다.

이진 트리 특징

• 정점이 N개인 이진트리는 최악의 경우 높이가 N이 될 수 있다.(편향 이진 트리)
• 정점이 N개인 포화 도는 완전 이진트리의 높이는 logN이다.
• 높이가 h인 포화 이진 트리는 2^2 - 1개의 정점을 갖는다.
• 일반벅인 이진 트리를 사용하는 경우는 많지 않다. 다음 자료구조에 응용된다.
  • 이진 탐색 트리
  • 힙
  • AVL 트리
  • 레드블랙트리

이진트리 노드 관계

왼쪽 자식 노드 인덱스 = 부모 인덱스 * 2
오른쪽 자식 노드 인덱스 = 부모 인덱스 * 2 + 1
부모 인덱스 = floor(자식 인덱스 / 2) // 왼쪽 자식이든 오른쪽 자식이든 2로 나눈 몫이 부모인덱스

이진 트리 구현

• 배열을 이용한 이진트리 표현

const tree = [
  undefined, // 0번 인덱스는 편의상 비운다.
  9,
  3, 8,
  2, 5, undefined, 7
  undefined, undefined, undefined, 4
]

• 링크드 리스트를 이용한 표현

class QueueNode {
  constructor(value) {
    this.value = value;
    this.next = null;
  }
}

class Queue {
  constructor() {
    this.head = null;
    this.tail = null;
    this.size = 0;
  }

  enqueue = newValue => {
    const newNode = new QueueNode(newValue);

    if (this.head === null) {
      this.head = this.tail = newNode;
    } else {
      this.tail.next = newNode;
      this.tail = newNode;
    }
    this.size += 1;
  };

  dequeue = () => {
    const value = this.head.value;
    this.head = this.head.next;
    this.size -= 1;
    return value;
  };

  peek = () => {
    return this.head.value;
  };

  display = () => {
    let currNode = this.head;
    let displayString = '[';

    while (currNode !== null) {
      displayString += `${currNode.value}, `;
      currNode = currNode.next;
    }
    displayString = displayString.substr(0, displayString.length - 2);
    displayString += ']';
    console.log(displayString);
  };
}

class TreeNode {
  constructor(value) {
    this.value = value;
    this.left = null;
    this.right = null;
  }
}

class Tree {
  constructor(node) {
    this.root = node;
  }

  display = () => {
    // level Order, bfs
    const queue = new Queue();
    queue.enqueue(this.root);

    while (queue.size) {
      const currNode = queue.dequeue();
      console.log(currNode.value);
      if (currNode.left) queue.enqueue(currNode.left);
      if (currNode.right) queue.enqueue(currNode.right);
    }
  };

  preOrder = (node = this.root) => { // 전위순회
    console.log(node.value);
    if (node.left) this.preOrder(node.left);
    if (node.right) this.preOrder(node.right);
  };

  inOrder = (node = this.root) => { // 중위순회
    if (node.left) this.inOrder(node.left);
    console.log(node.value);
    if (node.right) this.inOrder(node.right);
  };

  postOrder = (node = this.root) => { // 후위순회
    if (node.left) this.inOrder(node.left);
    if (node.right) this.inOrder(node.right);
    console.log(node.value);
  };
}

const tree = new Tree(new TreeNode(9));
tree.root.left = new TreeNode(3);
tree.root.right = new TreeNode(8);
tree.root.left.left = new TreeNode(2);
tree.root.left.right = new TreeNode(5);
tree.root.right.right = new TreeNode(7);
tree.root.left.right.right = new TreeNode(4);
tree.display();
tree.preOrder();
tree.inOrder();
tree.postOrder();

Queue 생성자는 이전에 학습했던 내용을 참고하자.

전위순회 preOder

1. 노드 방문
2. 좌측 자식노드에서 재귀
3. 우측 자식노드에서 재귀

중위순회 inOrder

1. 좌측 자식노드에서 재귀
2. 노드 방문
3. 우측 자식노드에서 재귀

후위순회 postOrder

1. 좌측 자식노드에서 재귀
2. 우측 자식노드에서 재귀
3. 노드 방문

힙

힙을 알아보기 전에 우선순위 큐를 먼저 알아보자!!

우선순위큐

우선순위가 높은 요소가 먼저 나가는 큐 (자료구조가 아닌 개념!)

힙이란?

이진 트리 형태를 가지며 우선순위가 높은 요소가 먼저 나가기 위해 요소가 삽입, 삭제될 대 바로 정렬되는 특징이 있다.

힙은 완전 이진 트리의 구조이다.

우선순위와 힙이 같아 보이지만 다르다! (우선순위 큐 != 힙)

힙의 특징

• 우선순위가 높은 요소가 먼저 나간다.
• 루트가 가장 큰 값이 되는 최대힙, 루트가 가장 작은 값인 최소힙이 있다.
• 자바스크립트에서는 직접 구현을 해야한다....😂

힙 동작 (최대힙이라고 가정)

힙 요소 추가 : 가장 마지막 정점에 추가 ➡️ 부모보다 크다면 히피파이(자리바꾸기) ➡️ 반복 ➡️ 최종적으로 루트가 가장 높은 정점이 된다. (O(logN)시간 복잡도)

힙 요소 삭제 (요소 제거는 루트만 가능) : 루트 정점 제거 ➡️ 가장 마지막 정점이 루트로 이동 ➡️ 두 자식이 작을 때까지 히피파이(자리바꾸기) 반복 ➡️ 최종적으로 힙 완성 (O(logN)시간 복잡도)

힙 구현

class MaxHeap {
  constructor() {
    this.heap = [null];
  }

  push = value => {
    // 힙 요소 추가
    this.heap.push(value);
    let currIndex = this.heap.length - 1;
    let parentIndex = Math.floor(currIndex / 2);

    while (parentIndex !== 0 && this.heap[parentIndex] < value) {
      const temp = this.heap[parentIndex];
      this.heap[parentIndex] = value;
      this.heap[currIndex] = temp;

      currIndex = parentIndex;
      parentIndex = Math.floor(currIndex / 2);
    }
  };

  pop = () => {
    // 힙 요소 삭제
    const retunrValue = this.heap[1];
    this.heap[1] = this.heap.pop();

    let currIndex = 1;
    let leftIndex = 2;
    let rightIndex = 3;

    while (
      this.heap[currIndex] < this.heap[leftIndex] ||
      this.heap[currIndex] < this.heap[rightIndex]
    ) {
      if (this.heap[currIndex] < this.heap[rightIndex]) {
        // 오른쪽 자식과 히피파이
        const temp = this.heap[currIndex];
        this.heap[currIndex] = this.heap[rightIndex];
        this.heap[rightIndex] = temp;
        currIndex = rightIndex;
      } else {
        // 왼쪽 자식과 히피파이
        const temp = this.heap[currIndex];
        this.heap[currIndex] = this.heap[leftIndex];
        this.heap[leftIndex] = temp;
        currIndex = leftIndex;
      }
      leftIndex = currIndex * 2;
      rightIndex = currIndex * 2 + 1;
    }

    return retunrValue;
  };
}

// 힙 요소 추가 테스트
const heap = new MaxHeap();
heap.push(45);
heap.push(36);
heap.push(54);
heap.push(27);
heap.push(63);
console.log(heap.heap); // [ null, 45, 36, 54, 27, 63 ]

// 힙 요소 삭제 테스트
const arr = [];
arr.push(heap.pop());
arr.push(heap.pop());
arr.push(heap.pop());
arr.push(heap.pop());
arr.push(heap.pop());
console.log(arr); // [ 63, 45, 36, 54, 27 ] - 힙 정렬

트라이

구글, 네이버에서 검색시 자동완성을 하려면 어떻게 해야할까??

트라이를 사용하면 된다!

트라이란?

문자열을 저장하고 효유적으로 탐새갛기 위한 트리 형태의 자료구조

자식 노드가 부모노드에서 부터 추가되는 단어를 포함하여 저장하고 있다.

루트의 오른쪽 자식을 살펴보면 모든 자식 노드들이 t로 시작하는 단어로 포함하게 된다.

이런식으로 우리가 미리 정의한 문자열로 자동완성을 구현할 수 있다.

트라이 특징

• 검색어 자동완성, 사전 찾기 등에 응용할 수 있따.
• 문자열을 탐색할 때 단순하게 비교하는 것보다 효율적으로 찾을 수 있다.
• L이 문자열의 길이일 때 탐색, 삽입은 O(L)만큼 걸린다.
• 대신 각 정점이 자식에 대한 링크를 전부 가지고 있기 때문에 저장 공간을 더 많이 사용한다.

트라이 구조

• 루트느 닙어있다.
• 각 간선(링크)은 추가될 문자를 키로 갖는다.
• 각 노드는 이전 노드의 값 + 간선의 키를 값으로 갖는다.
• 해시 테이블과 연결 리스트를 이용하여 구현할 수 있다.

트라이 구현

내가 지정한 단어를 트라이에 저장하는 방식이다.

예를들어 cat과 can 이라는 단어를 하나의 트라이에 저장하면 아래 이미지와 같다.

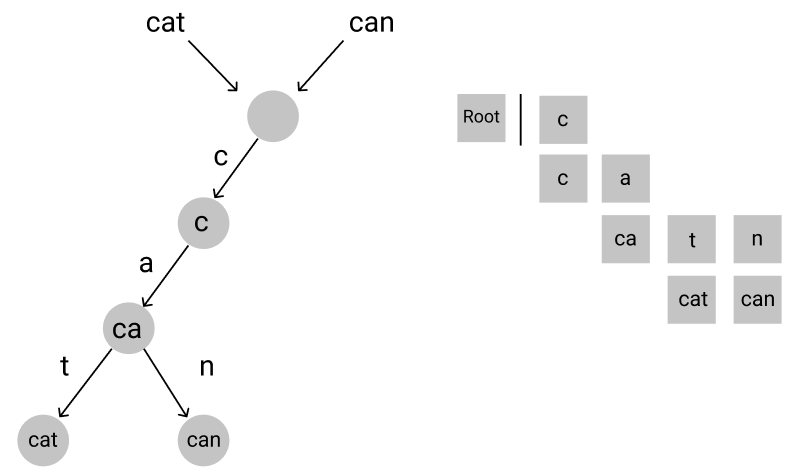
트라이 코드 구현

class QueueNode {
  constructor(value) {
    this.value = value;
    this.next = null;
  }
}

class Queue {
  constructor() {
    this.head = null;
    this.tail = null;
    this.size = 0;
  }

  enqueue = newValue => {
    const newNode = new QueueNode(newValue);

    if (this.head === null) {
      this.head = this.tail = newNode;
    } else {
      this.tail.next = newNode;
      this.tail = newNode;
    }
    this.size += 1;
  };

  dequeue = () => {
    const value = this.head.value;
    this.head = this.head.next;
    this.size -= 1;
    return value;
  };

  peek = () => {
    return this.head.value;
  };

  display = () => {
    let currNode = this.head;
    let displayString = '[';

    while (currNode !== null) {
      displayString += `${currNode.value}, `;
      currNode = currNode.next;
    }
    displayString = displayString.substr(0, displayString.length - 2);
    displayString += ']';
    console.log(displayString);
  };
}

class TrieNode {
  constructor(value = '') {
    this.value = value;
    this.children = new Map();
  }
}

class Trie {
  constructor() {
    this.root = new TrieNode();
  }

  insert = word => {
    let currNode = this.root;

    for (const char of word) {
      if (!currNode.children.has(char)) {
        currNode.children.set(char, new TrieNode(currNode.value + char));
      }
      currNode = currNode.children.get(char);
    }
  };

  has = word => {
    let currNode = this.root;

    for (const char of word) {
      if (!currNode.children.has(char)) {
        return false;
      }
      currNode = currNode.children.get(char);
    }

    return true;
  };

  autoCompleteBFS = prefix => {
    const nodeQueue = new Queue();
    const recomendedWords = [];
    const startingNode = this.findNodeByPrefix(prefix);

    if (startingNode === null) {
      return [];
    }

    nodeQueue.enqueue(startingNode);

    while (nodeQueue.size > 0) {
      const { value: currNodeValue, children } = nodeQueue.dequeue();

      if (children.size > 0) {
        [...children.values()].forEach(childNode => {
          nodeQueue.enqueue(childNode);
        });
      } else {
        recomendedWords.push(currNodeValue);
      }
    }

    return recomendedWords;
  };

  autoCompleteDFS = prefix => {
    const nodeStack = [];
    const recomendedWords = [];
    const startingNode = this.findNodeByPrefix(prefix);

    if (startingNode === null) {
      return [];
    }

    nodeStack.push(startingNode);

    while (nodeStack.length > 0) {
      const { value: currNodeValue, children } = nodeStack.pop();

      if (children.size > 0) {
        [...children.values()].forEach(childNode => {
          nodeStack.push(childNode);
        });
      } else {
        recomendedWords.push(currNodeValue);
      }
    }

    return recomendedWords;
  };

  findNodeByPrefix = prefix => {
    let targetNode = this.root;

    for (const char of prefix) {
      if (targetNode.children.get(char)) {
        targetNode = targetNode.children.get(char);
      } else {
        return null;
      }
    }

    return targetNode;
  };
}

const trie = new Trie();
trie.insert('cat');
trie.insert('can');
trie.insert('cell');
trie.insert('bap');
trie.insert('dam');

// 자동완성 테스트 - BFS
console.log(trie.autoCompleteBFS('')); // cat can bap dam cell
console.log(trie.autoCompleteBFS('c')); // cat can cell
console.log(trie.autoCompleteBFS('ca')); // cat can
console.log(trie.autoCompleteBFS('ce')); // cell
console.log(trie.autoCompleteBFS('f')); // null

// 자동완성 테스트 - DFS
console.log(trie.autoCompleteDFS('')); // dam bap cell can cat
console.log(trie.autoCompleteDFS('c')); // cell can cat
console.log(trie.autoCompleteDFS('ca')); // can cat
console.log(trie.autoCompleteDFS('ce')); // cell
console.log(trie.autoCompleteDFS('f')); // null

정렬

정렬이란?

요소들을 일정한 순서대로 열거하는 알고리즘

정렬 특징

• 정렬의 기준은 사용자가 설정할 수 있다.
• 크게 비교식과 분산식 정렬로 나눌 수 있다.
• 배부분의 언어가 빌트인으로 제공해준다.
• 삽입, 선택, 버블, 머지, 힙, 퀵 정렬 등 다양한 정렬 방식이 존재한다.

어떤 정렬이 제일 빠를까?

대게 퀵정렬, 합병정렬이 가장 빠르다고 알고 있을것이다. 하지만 여러가지 정렬 방식은 어떤 상황이냐에 따라 유리한 면이 있기 때문에 무엇이 좋고 나쁘고가 없다.

정렬 알고리즘 비교

비교식 정렬이란?

어떤 요소가 다른 요소와 비교를 하면서 정렬하는 방식

• 버블정렬 O(n^2)
  • 서로 인접한 두 요소를 검사하여 정렬하는 알고리즘
• 선택정렬 O(n^2)
  • 선택한 요소와 가장 우선순위가 높은 요소를 교환하는 정렬 알고리즘
• 삽입정렬 O(n^2)
  • 선택한 요소를 삽입할 수 있는 위치를 찾아 삽입하는 방식의 정렬 알고리즘(상대적으로 복잡)
  • 복잡해보이지만 어느정도 정렬이 되어있다면 퀵정렬보다 빠를수 있다.

분산식 정렬

요소를 분산하여 정렬하는 방식

분산식 정렬의 핵심 개념

분할정복

문제를 작은 2개의 문제로 분리하고 더 이상 분리가 불가능 할 때 처리한 후 합치는 전략으로 다양한 알고리즘에 응용된다.

• 합병정렬 O(nlogn)
  • 분할 정복 알고리즘을 이용한 최선과 최악이 같은 안정적인 정렬 알고리즘
• 퀵 정렬 O(nlogn), 최악의 경우 O(n^2)
  • 분할 정복 알고리즘을 이용한 매우 빠르지만 최악의 경우가 존재하는 불안정 정렬

자바스크립트에서의 정렬

const arr = [5, 9, 10, 3, 8, 3, 2];

arr.sort();
console.log(arr); // 10, 2, 3, 3, 5, 8, 9
// 아스키 코드를 기준으로 정렬하기 때문에 예상과 다르게 정렬된다.
// 10이 먼저 나오는 이유는 아스키문자 `1`이 `2`보다 작기 때문이다.(마치 사전정렬 처럼 동작)

arr.sort((a, b) => a - b) // 오름차순 정렬
console.log(arr); // 2, 3, 3, 5, 8, 9, 10

arr.sort((a, b) => b - a) // 내림차순 정렬
console.log(arr); // 10, 9, 8, 5, 3, 3, 2

주의!

요소의 아스키코드를 기준으로 정렬된다.

따라서 숫자를 올바르게 정렬을 하려면 sort 메서드의 콜백함수로 두 요소를 비교는 함수를 전달해줘야한다.

비교함수의 리턴값 (인자가 순서대로 a, b 일 때)

• 리턴값이 음수이면 a가 b보다 앞에 오도록 정렬

• 리턴값이 양수이면 b가 a보다 앞에 오도록 정렬

• 리텅갑싱 0이면 a와 b 순서 변경하지 않는다.

이진탐색

선형탐색

순서대로 하나씩 찾는 탐색 알고리즘, O(n) 시간 복잡도

이진탐색

정렬 되어있는 요소들을 반씩 제외하며 찾는 알고리즘, O(logn) 시간복잡도

이진탐색 특징

• 반드시 정렬이 되어있어야 사용이 가능ㅎ다.
• 배열 혹은 이진 트리를 이용하여 구현할 수 있다.
• O(logn) 시간복잡도 만큼 상당히 빠르다.

배열을 이용한 이진 탐색 구현

배열을 이용하게 되면 중간에 값을 추가하거나, 삭제할 때 선형시간이 걸리는 단점이 있는데

이 단점을 해소하기 위해 이진 탐색트리를 이용하여 구현한다.

이진 탐색 트리를 이용한 이진 탐색 구현

이진 탐색을 위한 이진 트리로 왼쪽 서브 트리는 루트보다 작은 값이 모여있고 오른쪽 서브 트리는 루트보다 큰 값이 모여있다.

이진 탐색 트리 문제점

이진 탐색 트리가 한쪽으로 편향된다면 순차 탐색과 동일하 시간 복잡도(O(n))를 갖게된다.

이를 해결하기 위해 AVL트리, 레드-블랙 트리 기법을 사용한다.

이진탐색 구현

• 배열로 이진 탐색 구현

// comming soon

• 이진탐색 트리로 이진탐색 구현

// cooming soon

과제

이진 탐색 트리의 요소 제거 부분을 작성해보세요. (조건 3개만 구현하면 된다.)

// comming soon

BFS, DFS

너비우선탐색

그래프 탐색 알고리즘으로 같은 깊이에 해당하는 정점부터 탐색하는 알고리즘

• Queue를 이용하여 구현한다.
• 시작지점에서 가까운 노드부터 탐색한다.
• v가 정점 수, e가 간선 수일 때, 시간복잡도는 O(v + e)이다.

깊이우선탐색

그래프 탐색 알고리즘으로 최대한 깊은 노드부터 탐색하는 알고리즘

• Stack, 재귀를 이용하여 구현한다.
• 시작 정점에서 깊은 것 부터 찾는다.
• v가 정점 수, e가 간선 수일 때, 시간복잡도는 O(v + e)이다.

그리디

매 선택에서 지금 이 순간 가장 최적인 답을 선택하는 알고리즘 따라서 최적해를 보장해주지는 않는다.

• 보통 최적해를 구하는 알고리즘보다 빠른 경우가 많다.
• 크루스칼, 다익스트라 알고리즘 등에 사용된다.
• 직관적인 문제 풀이에 적합하다.

그리디 대표 문제 - 거스름돈 반환하기

손님이 3140원짜리 물건을 구매하기 위해 5000원짜리 지폐를 주었을 때 어떤 1000원, 500원, 100원, 50원, 10원을 어떻게 조합해서 주는게 가장 좋을까?

A) 가장 큰 금액의 단위인 1000원부터 1개, 500원 1개, 100원 3개, 50원 1개, 10원 1개 순으로 거슬러준다.

코테 준비 방법

알고리즘을 잘 공부하는 법

문제풀 때

1. 항상 여러가지 풀이 방법이 있을 수 있으니 다양한 접근방식으로 풀어보자.
2. 항상 예외가 있을 수 있다는 것을 기억하자.
3. 내가 풀어낸 답이 베스트인지 의심하자.
4. 문제를 풀었다면 시행착오를 모두 기록하자.
5. 다른 사람의 코드를 많이보자. 생각하지 못했던 방법을 발견할 수 있다.
6. 쉽게 포기하지말고 도저히 모르면 답을 보는것도 좋다.

코딩 테스트 잘 보는 법

자신의 성향을 파악하자.

• 미리 생각하고 의사코드를 작성해야 더 잘 푸는 사람
• 일단 코드를 작성하면서 생각해야 더 잘 푸는 사람

메모하기

• 기잔하면 내가 무엇을 하려했는지 잊어먹는다.
• 코드에 주석을 달거나 노트에 메모를 하면서 풀자.
• 알고리즘은 논리적으로 표현할 수 있다. 헷가릴면 순서도를 그리면서 정리하자.

디버깅은 필수

• 내가 예상한대로 동작이 안된다면 꼭 디버깅을 하자.
• 로직 중간에 console.log 를 사용하여 값이 정상적인지 확인하자.
• 외부 IDE 사용이 가능하다면 Node.js의 디버그 모드를 사용하자.

익숙해지기

• 문제에는 너무 많은 정보가 있다.
• 문제를 잘 읽고 중요한 정보만 잘 읽는 것에 익숙해져야 한다.
• 시간 복잡도를 계산하는 것에 익숙해져야 한다.
  • 자잘자잘한 성능보다 시간복잡도가 훨신 중요한다.
• 항상 엣지 케이스르 생각하는 것에 익숙해져야 한다.

좋은 코드를 만드는 법

간결하고 가독성 좋은 코드

• 변수, 함수의 이름을 잘 정했는가?
• 중복 코드를 제거했는가?
• 함수형 프로그래밍도 좋은 방법
  • map, filter, reduce와 같은 고차함수를 이용하기

가지치기를 했는가?

• 흔히 가지치기는 백트래킹과 같은 알고리즘에서 사용되지만 그 외 알고리즘에서도 중요하다.
• 사소한 로직이라면 성능이 크게 개선되지는 않지만 코드 리뷰에서 좋은 평가를 받을 수 있다.

자바스크립트를 잘이용하고 사용했는가?

• 자바스크립트 문법을 잘 활용하자.
• ex) 구조분해할당, 스프레드 오퍼레이터

일관성을 유지했는가?

• 잘 잣더라도 일관성 없는 코드보다 조금 더러워도 일관성있는 코드가 좋다.
  • var와 let혼용
  • 스네이크케이스, 카멜케이스 혼용
  • 변수명 함수명 줄임말로 쓰다가 어딘가에서 전부 적는 경우
• 제출전에 코드 스타일이나 변수명, 함수명을 꼭 확인해보자.

만약 코드를 안보는 코딩 테스트라면 스타일은 무시하고 풀자!!!

대부분의 대기업에서 공채 코테는 코드를 살펴보지는 않는다.

comment

오늘 TIL 작성을 시작하기전에 TIL을 기존 보다 더욱 간결하게 핵심만 작성해서 양을 줄이고 작성 시간을 줄이는것을 목표했다....

하지만 똑 정리하다보니 방대하게 작성하게 된 것 같다. 내일은 조금 더 대범하게 거두절미하고 팍팍 처내면서 작성해봐야겠다. (하루의 시간이 너무 소중한것을 깨닳게 해주는 프로그래머 웹 데브코스 🤣)

다른 자료구조와 알고리즘이 이전에 학습했던 경험이 있어서 매우 익숙했다. 하지만 오랜만에 다시 학습하다보니 다시 리마인드 하기에 너무 좋은 장치가 되었다.

또한 새로 알게된 개념은 기존에 트라이 라는 알고리즘에 대해 학습했던 적이 없었는데 이번 기회에 새로 알게되었고 트라이는 문자열 자동완성에서 활용된다는 점에서 매우 흥미로웠다👀

아직 TIL 중간중간 구현해야하는 코드와 과제를 마무리 하지 못했는데 완성되는대로 업데이트 해보자