[BOJ] DFS(백트래킹): N과 M(1) (15649)★

문제
자연수 N과 M이 주어졌을 때, 아래 조건을 만족하는 길이가 M인 수열을 모두 구하는 프로그램을 작성하시오.

1부터 N까지 자연수 중에서 중복 없이 M개를 고른 수열

입력
첫째 줄에 자연수 N과 M이 주어진다. (1 ≤ M ≤ N ≤ 8)

출력
한 줄에 하나씩 문제의 조건을 만족하는 수열을 출력한다. 중복되는 수열을 여러 번 출력하면 안되며, 각 수열은 공백으로 구분해서 출력해야 한다.

수열은 사전 순으로 증가하는 순서로 출력해야 한다.

입출력예시

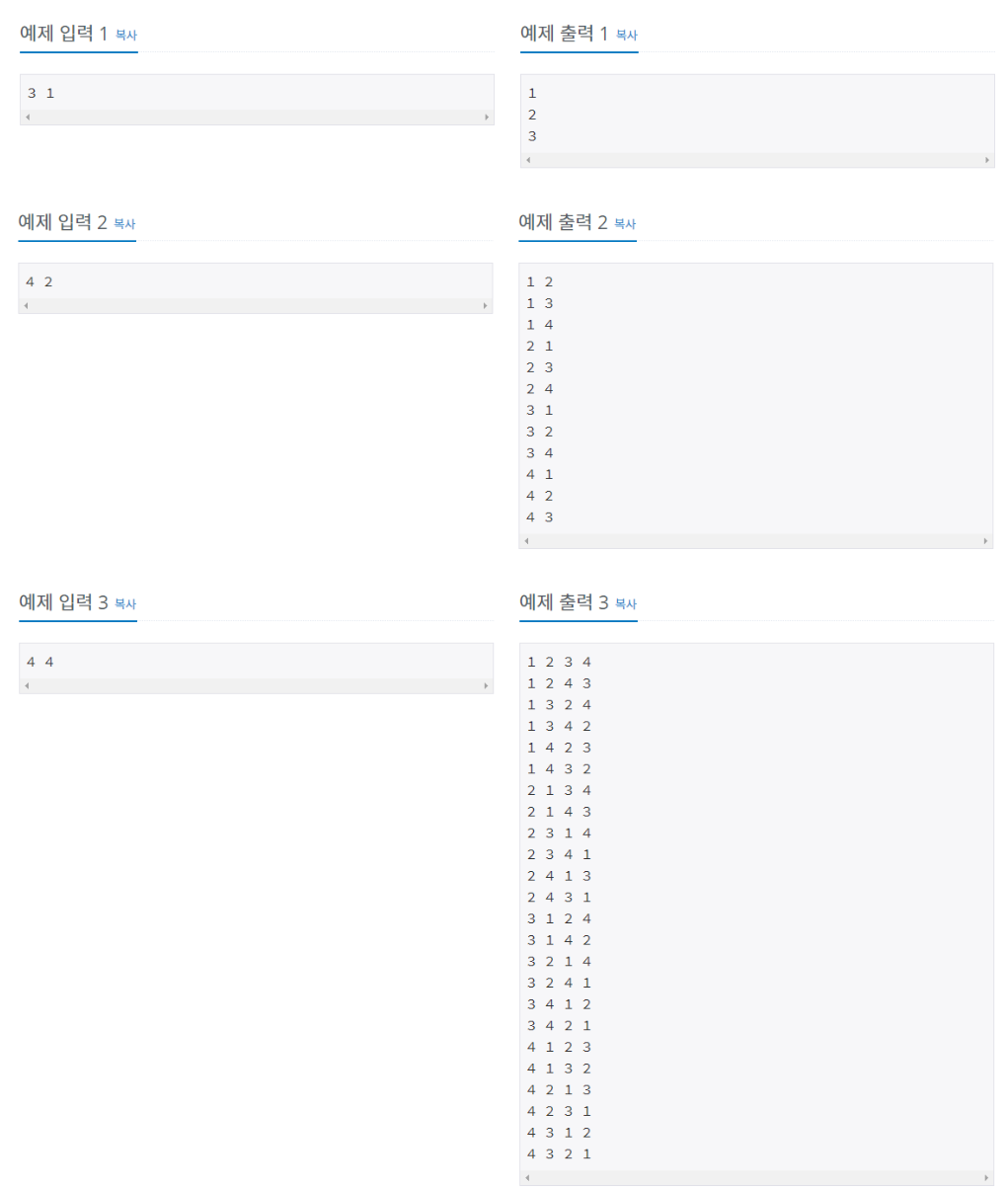
시도

• 정답은 나오지만 runtime error 발생

# itertools의 combination은 순서에 따라 중복X
# itertools의 permutations은 순서 상관없이 중복O

from itertools import permutations as p

n, m = map(int, input().split(' '))
n, m = 4, 2
lst = [x for x in range(1, n+1)]
for i in  p(lst,m):
    print(i[0], i[1])

정답코드1 : itertools 활용

from itertools import permutations as p

n, m = map(int, input().split(' '))
n, m = 4, 2

lst = [x for x in range(1, n+1)]
lst_p = list(p(lst, m))

for i in range(len(lst_p)):
    for j in range(m):
        print(lst_p[i][j], end = " ")
    print()

정답코드2 : 백트래킹 활용

n, m = 3, 2
def dfs():
    if len(lst) == m:
        print(' '.join(map(str,lst)))
        return
    for i in range(1, n+1):
        if i not in lst:
            lst.append(i)
            dfs()
            lst.pop()
dfs()

백트래킹은 DFS에 기반한 응용 알고리즘으로,
주어진 문제의 답을 구하기 위해 현재 상태에서 가능한 모든 후보군을 따라가며 탐색하는 알고리즘이다.
BOJ의 N과 M (1~9) 시리즈가 백트래킹 연습에 아주 적합하다.

• 백트래킹을 기반으로 재귀함수를 다시 이해하려 코드 수행 순서를 정리했다.

FIRST MAIN LOOP #############################################################

dfs1 : i == 1 : [1]     # append 1

dfs2 : i == 1 : ----------------

dfs2 : i == 2 : [1,2]   # append 2
dfs3 : return [1,2]
dfs2 : i == 2 : [1]     # pop 2

dfs2 : i == 3 : [1,3]   # append 3
dfs4 : return [1,3]
dfs2 : i == 3 : [1]     # pop 3

dfs1 : i == 1 : []      # pop 1

SECOND MAIN LOOP #############################################################

dfs1 : i == 2 : [2]     # append 2

dfs5 : i == 1 : [2,1]   # append 1
dfs6 : return [2,1]
dfs5 : i == 1 : [2]     # pop 1

dfs5 : i == 2 : ----------------

dfs5 : i == 3 : [2,3]   # append 3
dfs7 : return [2,3]
dfs5 : i == 3 : [2]     # pop 3

dfs1 : i == 2 : []      # pop 2

THIRD MAIN LOOP #############################################################

dfs1 : i == 3 : [3]     # append 3

dfs8 : i == 1 : [3,1]   # append 1
dfs9 : return [3,1]
dfs8 : i == 1 : [3]     # pop 1

dfs8 : i == 2 : [3,2]   # append 2
dfs10: return [3,2]
dfs8 : i == 2 : [3]     # pop 2

dfs8 : i == 3 : -----------------

dfs1 : i == 3 : []      # pop 3

#############################################################