[이코테] 투 포인터/구간합 ★

배열의 특정 연속된 구간을 처리하는 경우

• 문제에서 연속된 데이터 구간을 처리하기 원한다면

예시1

• 자연수로 구성된 수열에서 합이 x인 부분 연속 수열의 개수를 구하시오

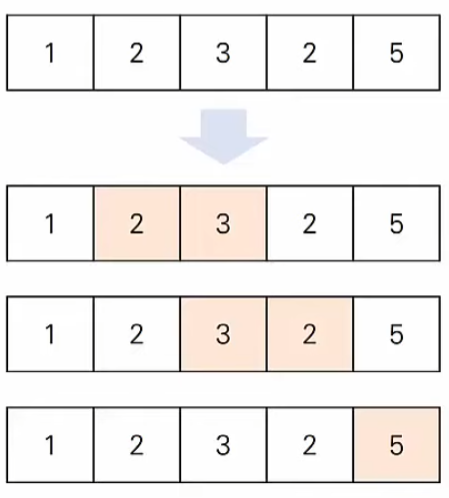
예시2

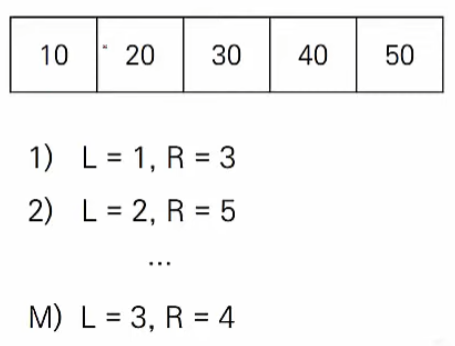
• N 개의 정수로 구성된 수열이 있다.
• [L, R]로 구성된 M개의 쿼리 정보가 주어졌을 때, 각 쿼리에 해당하는 데이터의 합을 모두 구하시오

두 예시 모두 일반적인 슬라이딩 윈도우나 중첩 loop를 사용하면 해결할 수 있지만, O(N^2) 의 시간 복잡도를 가진다.
아래 두 가지 기법을 활용하면 이러한 유형의 문제는 O(N)으로 해결이 가능하다.

문제 해결 기법(중요)
1. Two Pointers (투 포인터)
2. Interval Sum (구간 합)

Two Pointers

코드

• Two Pointers를 구현하는 코드는 다양하다. 두번 째 코드에서는 start와 end를 모두 제어할 수 있기 때문에 더 많은 경우에 활용이 가능한 것 같다.

• 첫번째 방법

n, m = 5,5
data = [1,2,3,4,5]

result = 0
temp_sum = 0
end = 0

for start in range(n):
	
    # 목표치(m)에 다다를때까지 end 증가시키기
    while temp_sum < m and end < n :
    	temp_sum += data[end]
        end += 1
        
    # 목표치에 도달
    if temp_sum == m:
    	result += 1
    
    # 다음 loop에 start가 한 칸 앞으로 오니 해당 숫자 빼주기
    temp_sum -= data[start]

2. 두 번째 방법

n, m = 5,5
data = [1,2,3,4,5]

result = 0
temp_sum = 0
start = 0
end = 0

# 리스트 길이보다 작은 경우
while end < n:
    
    # 데이터 추가
    temp_sum += data[end]
	
    # 목표치를 넘는 경우 가능할때까지 최소화
    while temp_sum > m:
        temp_sum -= data[start]
        start += 1
	# 목표치에 도달
    if temp_sum == m:
        result += 1
        
	# 다음 루프를 위해 데이터 추가
    end += 1

Interval Sum

• 접두사 합(Prefix Sum)을 활용하면 N(N+M)의 시간복잡도로 구현 할 수 있다.

코드

n = 5
data = [10, 20, 30, 40, 50]

# Prefix sum 계산
temp_sum = 0
prefix_sum = [0]
for d in data:
	temp_sum += d
    prefix_sum.append(temp_sum)

# Interval Sum 계산
left = 3
right = 4
print(predix_sum[right] - prefix_sum[left-1]

출처: 이코테 https://www.youtube.com/watch?v=rI8NRQsAS_s&list=PLRx0vPvlEmdAZ6xXAUyBbLQa2-Ideakb-