거리두기 확인하기

링크: https://www.acmicpc.net/problem/1149
문제분류 : 다이나믹 프로그래밍
난이도 : 실버1
풀이시간 : 30~40분
결과: 성공

회고

전형적인 DP문제였다. DP 안푼지 하도 오래되어 걱정이 됐는데, 풀다보니 익숙해졌다!
예전에 바킹독시리즈 따라가다가 백엔드 데브코스에 붙어서 바킹독 시리즈를 잠시 놓았다.
프로그래머스 문제와 바킹독 시리즈를 병행하는 기념으로 안푼 문제 중에 몸 풀기로 풀어보았다.
그래도 첫 제출에 한 번도 안틀리고 바로 정답을 찾아서 기분 좋았다.
한 번에 풀리니 기분은 좋았다. 알고리즘 푸는 거 다시 좋아하게 될지도...?

내 코드

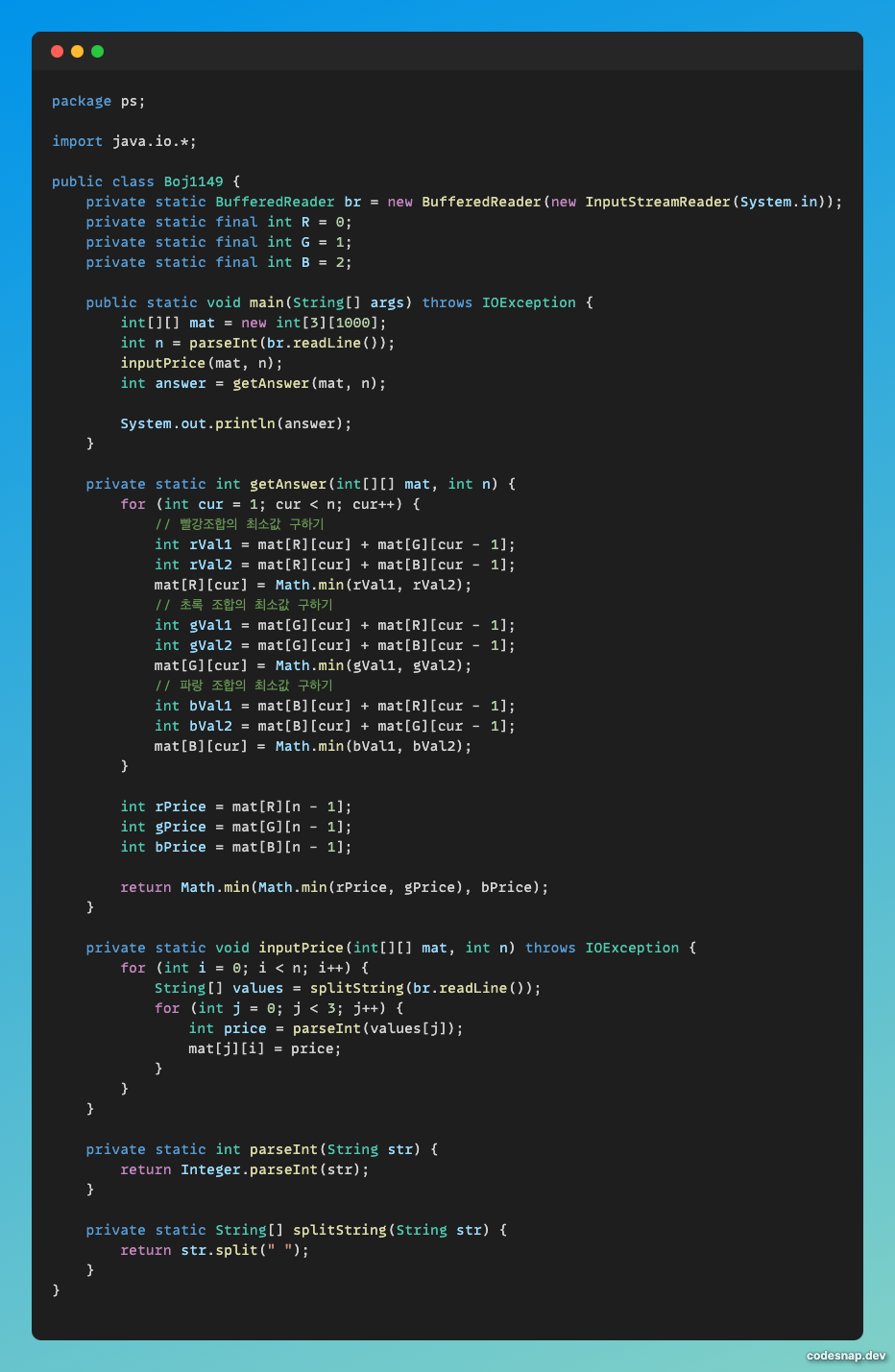
DP는 반복되는 점화식을 찾는 것이 관건인데, 이 문제는 금방 찾을 수 있었다.
우리의 목표는 규칙에 따라 최소비용을 찾는 것이다.
일반적으로 최소비용을 찾으려면 가장 적은 비용만 골라서(그리디하게) 더하면 되지만,
이 문제는 규칙이 있어 최소비용을 고르는데 제한 사항이 있다.
그렇기 때문에 그리디 알고리즘이 먹히지 않는다.
그렇다고 모든 조합을 다 따질 수 없다.
한 곳에 색칠할 수 있는 경우의 수는 3개이고 그 중 안되는 경우를 제외하면 된다.
하지만 이렇게 될 경우 시간 복잡도는 정수의 거듭제곱이 된다.

문제의 시간제한은 0.5초이고 1억을 1초라고 가정하자.
전체 길이는 최대 1000개이므로, 시간복잡도는 O(3^1000)이 된다.
이건 계산 안해봐도 1억은 가볍게 넘긴다. 따라서 완전탐색은 불가능하다.

이런 상황에서 가장 효과적인 방법은 DP이다.
처음 색을 칠하는 과정에서 하나씩 쌓아올려가며 가장 적은 비용을 찾아갈 수 있다.
처음 시작하는 색깔을 빨강, 초록, 파랑으로 놓고 비용을 찾는 규칙을 생각해봤다.

• 빨강 : 현재 칠하는 위치의 빨강의 비용 + 이전에 칠한 파랑의 비용 혹은 초록의 비용
• 초록 : 현재 칠하는 위치의 초록의 비용 + 이전에 칠한 빨강의 비용 혹은 파랑의 비용
• 파랑 : 현재 칠하는 위치의 파랑의 비용 + 이전에 칠한 빨강의 비용 혹은 초록의 비용

각 색깔 별로 2개의 비용이 나오는데 그 중 최소 비용을 찾으면 된다.
그 최소 비용을 가지고 같은 규칙으로 계속해서 쌓아 올려가면
결국 빨강, 초록, 파랑에서 나올 수 있는 조합의 총 최소비용이 나온다.
그리고 그 세 개의 최소 비용 중에 가장 작은 비용이 우리가 얻고자 하는 정답이다.

모범답안

모범답안 링크: https://github.com/encrypted-def/basic-algo-lecture/blob/master/0x10/solutions/1149.cpp

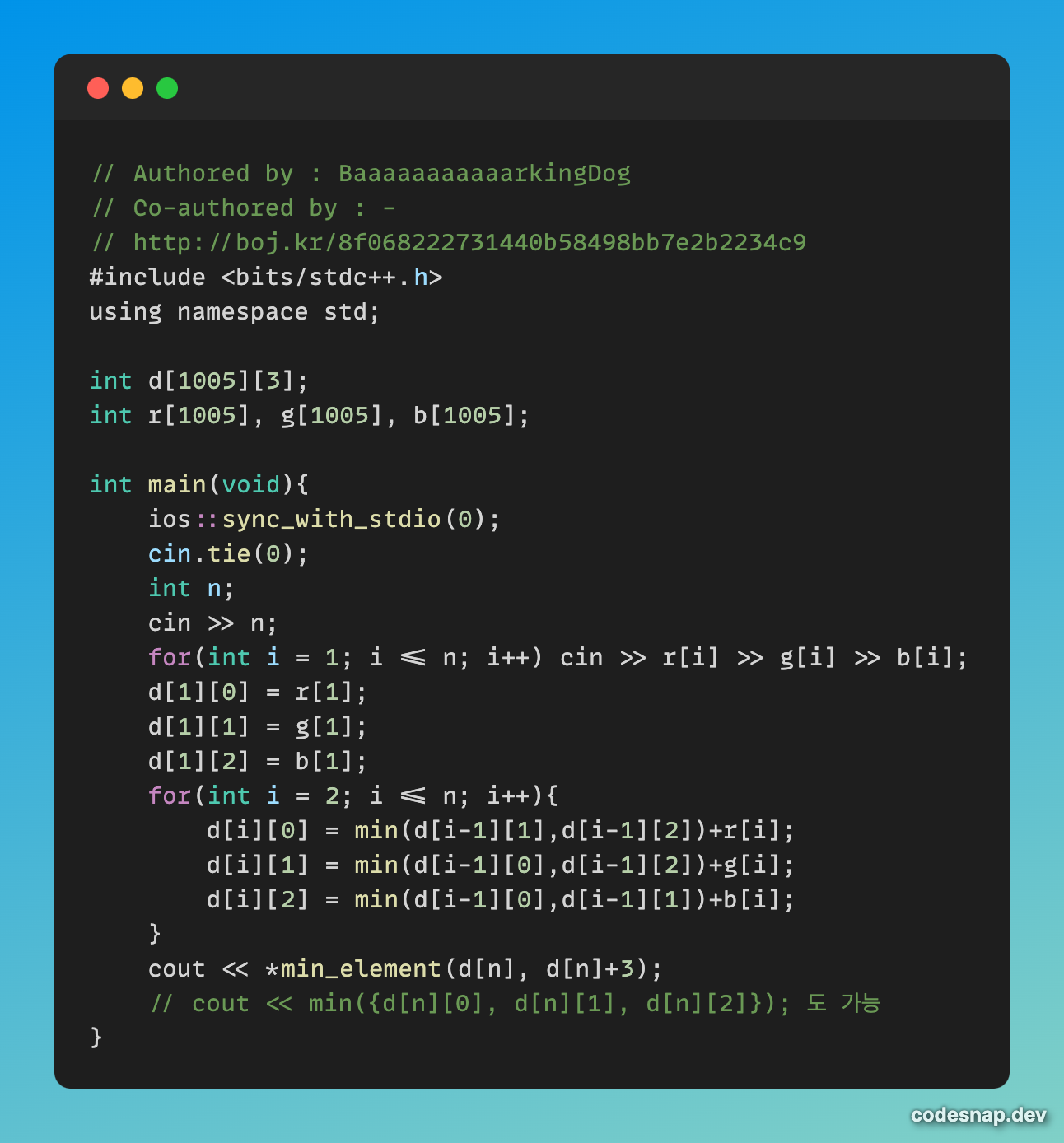
바킹독 시리즈는 C++코드를 기준으로 해답이 작성되었다.
나는 복수전공하면서 C계열 언어를 많이 썼기 때문에 익숙해서 상관 없지만
C/C++에 익숙하지 않은 분들은 어려울지도 모르겠다.

내 코드와의 차이점이 크게 없다.
굳이 찾아본다면 내 코드는 rgb배열을 따로 안만들고 하나의 2차원 배열을 재활용해서 사용했다.
여기서는 r, g, b 배열을 따로 만들어 주었고 최소비용 테이블은 d라는 2차원 배열을 만들어서 답을 구했다.

내가 작성한 코드보다 더 효율적인 부분은
min에서 이전 비용 두 개 중 최소비용을 찾은 후 현재 위치의 비용을 더해준 것이다.
확실히 이렇게 구하는 것이 중복된 부분을 줄일 수 있고 좀 더 논리적인 방법인거 같다. 기억해두자.