
순위
링크: https://school.programmers.co.kr/learn/courses/30/lessons/49191
문제분류 : 그래프
난이도 : Level 3
결과: 실패
회고
문제풀이에 어려웠던 점은 권투 선수 한 명의 대전 결과를 모를 때 어떻게 순위를 정할지였다.
처음에는 승리/패배에 관한 관계만 알고 있다면 순위를 정할 수 있을 거라 생각했는데,
이 생각에 갖히다보니 도저히 방법이 생각이나지 않았다. 결국 답지를 보았고 풀이방법을 이해했다.
그래프 문제를 정복할겸, 문제풀이 아이디어를 기억해놓을 겸 블로그에 기록하기로 했다.
모범 답안
문제풀이 아이디어
이 문제에서 누가 몇 등인지는 중요하지 않다.
중요한 건 그 사람의 순위가 정해질 수 있는지 여부다. 답이 될 수 있는 과정도 필요 없다.
순위가 정해질 수 있는 조건만 된다면 답에 추가하면 된다.
그렇다면 순위가 정해지는 경우는 언제일까?
승리 횟수(이긴 사람 수) + 패배 횟수(진 사람 수) + 1(본인) == 총 인원이다.
구체적으로 두 가지 경우로 나뉜다.
1) 한 명의 사람이 모든 사람들과 경기한 결과가 있을 경우 정확하게 순위가 결정됨
2) 모든 경우가 없더라도 사람들의 시합 결과로 상대적으로 정해질 수 있음
2번 케이스가 가능한 이유는 문제설명에
'만약 A 선수가 B 선수보다 실력이 좋다면 A 선수는 B 선수를 항상 이깁니다.'
라는 조건 때문이다.
예를 들어 만일 선수1이 선수2를 이기고 선수2가 선수3을 이겼다고 해보자.
여기서 선수 1은 무조건 선수 3을 이긴다는 것을 알 수있다.
왜냐하면 선수 1은 선수 2보다 실력이 좋아 선수 2를 이겼다.
선수 2는 선수 3 보다 실력이 좋아 선수 3을 이겼다.
따라서 선수1은 선수3보다 실력이 좋고 둘의 시합 결과가 나와있지 않아도
선수1이 선수3을 이긴다는 걸 알 수 있다.
그래서 문제풀이는 아래와 같이 진행된다.
1) 시합에 참여하는 사람들 사이에 승리, 패배 관계를 설정한다. 이때 그래프를 사용한다.
2) 설정된 관계(그래프)를 가지고 승리 횟수, 패배 횟수를 센다.
3) 승리 횟수 + 패배 횟수 + 1이 n과 동일한 경우 answer에 1을 더한다.
4) 선수 마다 1~3 과정을 반복한다.
여기서 승리,패배 횟수를 셀 때 2번 케이스에 관해서도 체크해야만 한다.
그래서 재귀를 사용하여 구현한다. 자세한 건 코드로 알아보자.
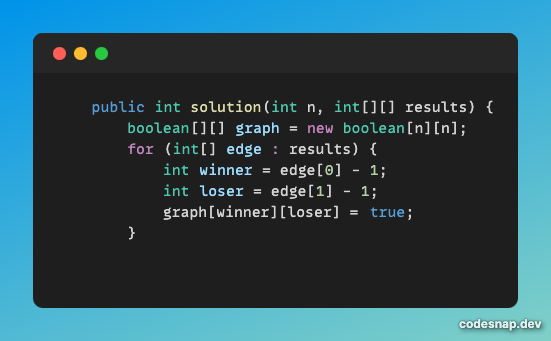
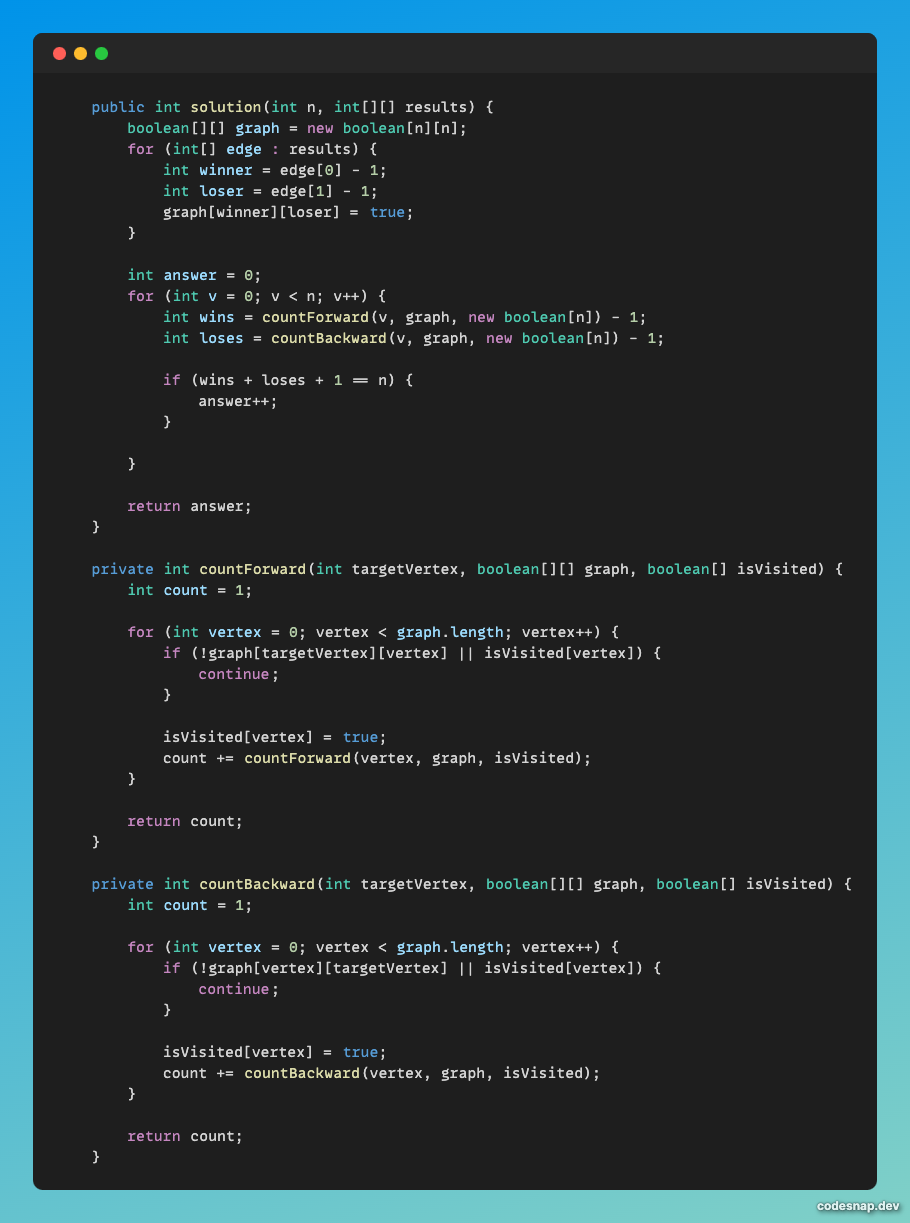
먼저 승리/패배 관계를 설정한다. 여기서는 인접행렬을 이용해 관계를 표현했다.
왜냐하면 복싱선수의 최대값이 100명으로 제한되어 있기 때문이다.
적은 데이터에 관해 쉽게 관계를 설정할 수 있는 인접행렬이 가성비 있는 구현방법이다.
관계는 2차원 배열 graph에 설정하였고,
row가 column에 승리했을 때를 true로 표현했다.
results의 0번은 승자, 1번은 패자이므로 위와 같은 코드가 나온다.
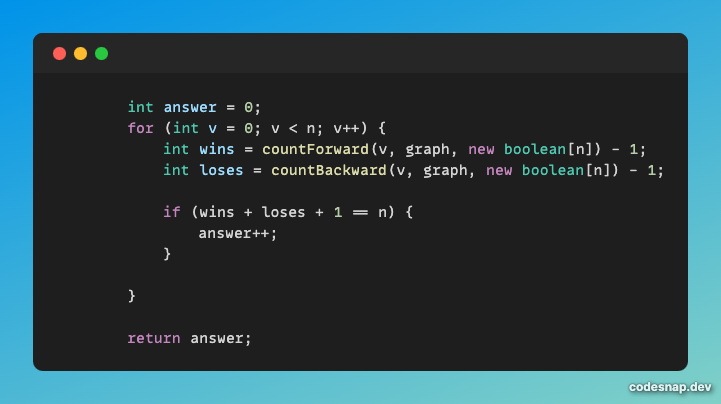
위의 코드는 유저간의 관계를 가지고 wins(이긴 횟수)와 loses(패배 횟수)를 체크하는 코드이다.
여기서 체크한 wins(이긴 횟수) + loses(패배 횟수) + 1(본인) == n일 경우 answer의 값을 1 올린다.
이 코드에서 countFoward메서드는 그래프 관계의 정방향 즉, 이긴 횟수를 체크,
countBackward메서드는 그래프 관계의 역방향 즉, 패배 횟수를 체크한다.
모든 복서들에 관해 탐색을 마치면 answer를 답으로 반환한다.
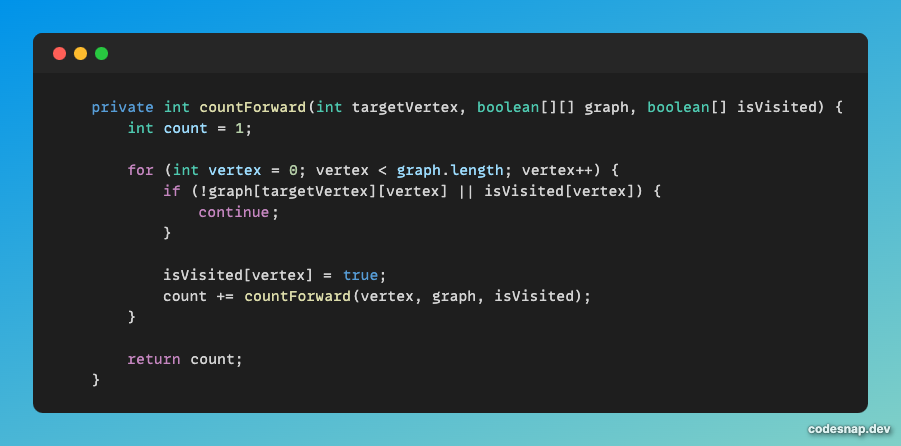
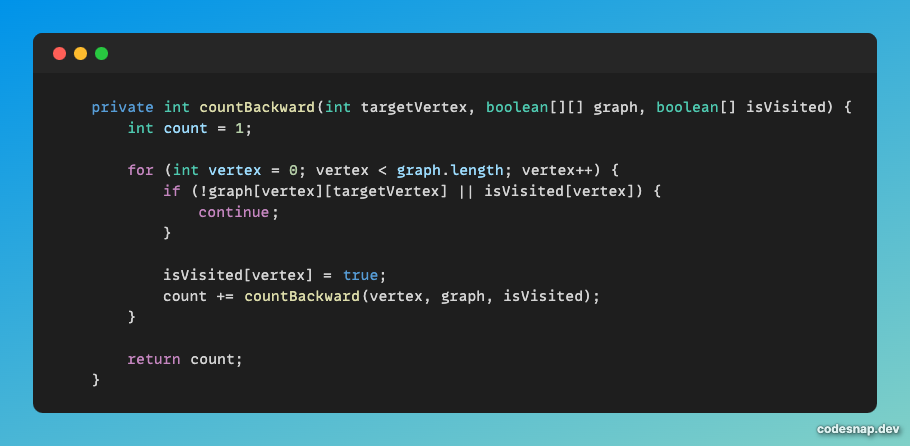
countFoward와 countBackward의 원리는 같다. 다만 방향만 다를 뿐이다.
그래서 countBackward를 기준으로 설명해보겠다.
아마 for 문에 관해서는 이해가 될거다. 한 명의 유저가 패배한 유저를 순서대로 체크한다.
isVisited를 true로 체크하는 건 한 번 체크한 유저와의 관계를 다시 체크하지 않기 위해서이다.
여기서 핵심은 재귀적으로 체크하는 로직이다.
재귀적으로 체크해야하는 이유는 상대적인 관계로 순서가 확정될 수 있는지 체크하기 위해서이다.
예제 테스트 케이스에서 5번은 2번에게 졌다. 2번은 1, 3, 4번에게 졌다.
따라서 승패의 절대적인 관계로 인해 5번은 1, 2, 3, 4번 모두에게 진 것이다.
5번은 승리횟수 0, 패배횟수 4이다.
따라서 승리횟수 + 패배횟수 + 1이 5이므로 정답 조건을 만족한다.
이 정도면 충분히 모든 코드를 이해했을 거라 생각한다. 전체적인 코드는 아래와 같다.
공부하면서 정리한 그래프에 관한 생각들
그래프가 필요한 순간
너무 당연한 말이지만, 스스로 정리해보았다.
그래프 자료구조는 데이터들 사이에 연관관계를 가지고 기능을 구현해야 할 때 사용한다.
인스타그램의 '함께 아는 유저'기능을 생각해보자.
인스타그램에서는 어떤 사람의 개인 페이지에 들어갔을 때,
함께 아는 유저가 있을 경우 어떻게 집계하면 될까?
1 ) 나의 팔로잉 리스트 가져온다.
2 ) 나의 팔로잉 리스트에 있는 한 명의 유저의 팔로잉 리스트를 가져온다.
3 ) 만일 그 팔로잉 리스트에 어떤 사람의 아이디가 있다면
즉, 어떤 사람을 팔로잉하고 있다면 '함께 아는 유저' 리스트에 넣는다.
4 ) 2와 3의 과정을 내가 팔로잉 하는 모든 유저에게 수행한다.이렇게 서로 연관되어 있는 유저들의 연관 관계를 저장해놓는다면, 쉽게 기능을 구현할 수 있다.
이뿐만 아니라 두 데이터 사이에 가중치를 줘야할 경우 사용한다.
두 데이터는 엣지를 통해 연결되기 때문에, 엣지에 가중치를 줄 수 있다.
대표적인 예는 네비게이션에서 도착지점까지의 최소비용 경로가 있다.
너무 대표적인 예시라 생략하겠다.
++ 인스타그램에서 '친한친구'에게만 스토리를 보여주는 기능에도 응용할 수 있을거 같다!
다른 자료구조와의 차이점
List는 관계 설정보다는 공통된 타입의 데이터들을 모아두는 방식이다.
물론 List도 그래프에 사용되지만 관련있는 데이터를 모으는데 사용된다.
관계에 관해서 디테일하게 설정해야할 경우 Edge가 필요하다.
Map은 특정 데이터를 빠르게 찾아야 할 경우 사용한다.
유니크한 데이터를 저장하고 빠르게 사용해야 할 경우(캐시성 데이터) 사용하면 좋다.
Set은 중복없이 데이터의 집합을 만들고 싶을 때 사용한다.
List와의 차이는 중복 데이터 저장 여부이다.
Tree도 물론 관계 설정에 사용할 수 있다.
하지만 루트 노드 혹은 특정 노드로부터 시작해 트리 레벨에 따라 접근을 한다는 점에서
양방향 관계 보다는 단방향, 하향식 관계를 설정하는데 좀 더 적합하다고 생각한다.
트리는 노드 사이에 순서가 존재한다. 그래서 데이터들을 연결하고 정렬할 경우 사용한다.
물론 엄밀히 말하면 특수한 그래프지만, 문제풀이를 할 때는 그래프와 구분하자.
TMI
나는 그래프 공포증(?)이 있다.
복수전공하면서 자료구조 수업에서 그래프를 처음 공부했다.
어디에 써야할 지 전혀 모르겠던 그래프를 C언어로 공부하고 구현하면서 많이 애먹었다.
결국 시험을 위해 자료구조의 목적을 잊은 채 전공서적의 코드를
아예 외워버렸던 기억이 난다.그래도 성적은 잘 받아야지요..ㅎㅎ
이러한 기억 덕분에 내게 '그래프' == '몰라 무서워 이게 뭐야'가 되었다.
그 후 취업준비를 위해 코딩테스트 문제를 풀 때도
문제를 취사선택하며 그래프가 나오는 문제를 요리조리 피해갔다.
이 문제를 블로그에 작성하고 회고하는 것을 계기로
부디 미래의 내가 그래프 자료구조와 관련된 알고리즘을 정복했길 바래본다!

부자시군요..