Problem Description
Given a directed acyclic graph (DAG) of n nodes labeled from 0 to n - 1, find all possible paths from node 0 to node n - 1 and return them in any order.
The graph is given as follows: graph[i] is a list of all nodes you can visit from node i (i.e., there is a directed edge from node i to node graph[i][j]).
Example
Example 1:
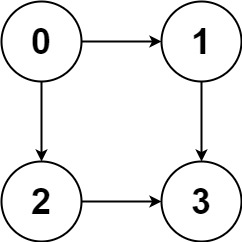
Input: graph = [[1,2],[3],[3],[]]
Output: [[0,1,3],[0,2,3]]
Explanation: There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.
Example 2:
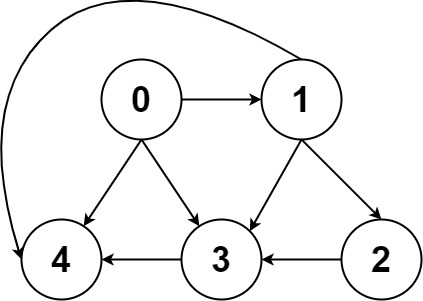
Input: graph = [[4,3,1],[3,2,4],[3],[4],[]]
Output: [[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]
Approach
For this problem, we want to start traversing from 0 until we reach the target node, which is equal to the size of the graph - 1. Hence, the base case would be when the last element of the curent collection is equal to the target node.
curr[-1] == (len(graph) - 1)
Then, we can enumerate through all the neighbor nodes of the current node. At the end of the iteration, we should reverse the choice by popping out the neighbor node from the path, so that we could start all over for the next neighbor node.
Solution
class Solution(object):
def allPathsSourceTarget(self, graph):
ans = []
def backtrack(curr):
if (curr[-1] == (len(graph) - 1)):
ans.append(curr[:])
return
nex = graph[curr[-1]]
for i in nex:
curr.append(i)
backtrack(curr)
curr.pop()
backtrack([0])
return ans