1027. Longest Arithmetic Subsequence

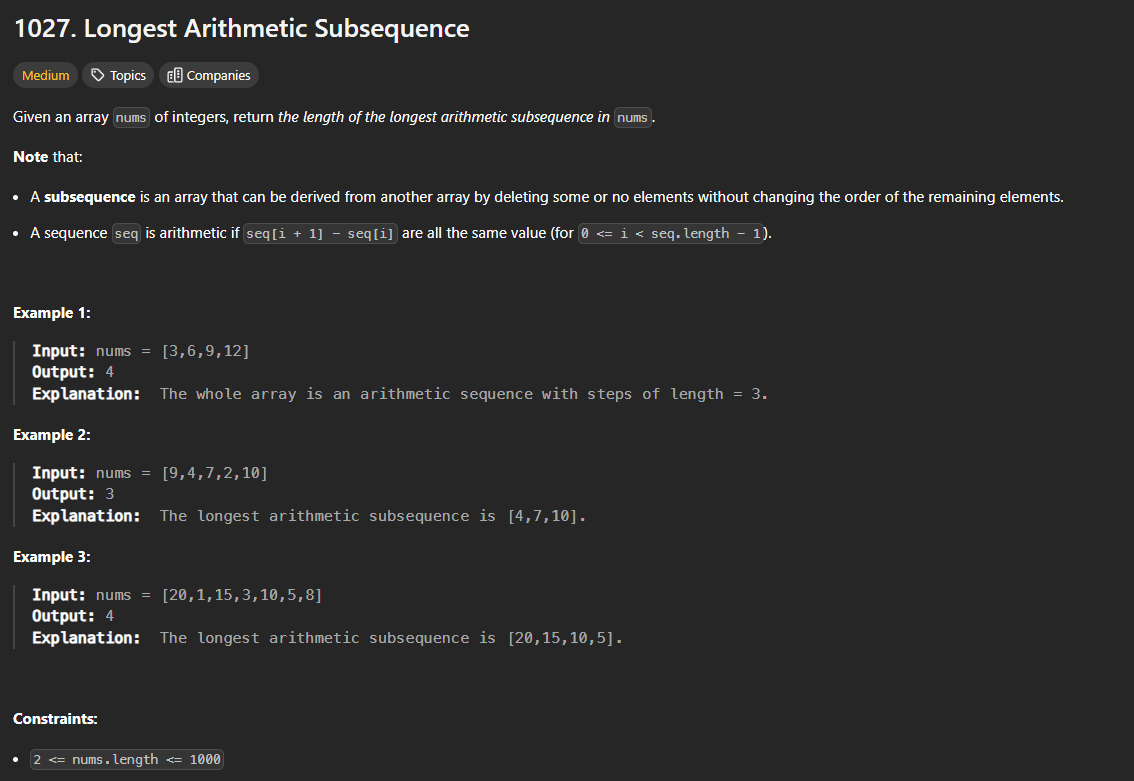
오늘도 어김 없이 DP 문제를 풀어봤는데 유독 이 문제는 잘 안풀려서 고민을 하였고 답을 보고도 잘 이해가 안갔기에 다시 풀 목적으로 기록을 해본다. 일단 Single DP 로도 풀 수 있지 않을까? 생각은 해봤는데 Single DP 로 풀경우에 테스트 케이스를 절대 다 통과하지 못했다. 왜 일까? 이유는 간단한데 Single DP 로는 필요한 값을 모두 저장하기 어렵기 때문이다.

의외로 유투브 영상에서 해답을 찾을 수 있었다. [9,4,7,2] 리스트가 있을 떄, longest difference 는 [4,7] 은 3이 될 수 있고 [9,7] 처럼 -2가 될 수 도 있다. 즉, 7의 인덱스에서 3이나 -2의 difference 를 전부 가질 수 있는 것이기 때문에 LIS 문제를 풀었던 것 처럼 내 앞에 있는 숫자가 가지고 있는 Longest difference 가능성을 전부 저장하고 합을 구해야지 최대 값이 나올 수 있다.

좀 어려운 문제라고 느꼈지만 그래도 패턴만 잘 익히면은 괜찮을 문제같기도 하다.

class Solution {
public:
    int longestArithSeqLength(vector<int>& nums) {
        map<int,map<int,int>> dp; 
        int max_ = 2; 
        for(int i = 1; i < nums.size(); i++){
            for(int j = 0; j < i; j++){
                int diff = nums[i] - nums[j]; 
                if(dp[j].count(diff)){
                    dp[i][diff] = max(dp[i][diff], dp[j][diff] + 1); 
                    max_ = max(max_, dp[i][diff]); 
                } else{
                    dp[i][diff] = 2; 
                }
            }
        }
        return max_; 
    }
};