All Paths from Source Lead to Destination

예전에 한참 못풀던 문제였는데 Topological Sort의 개념을 조금씩 이해하다보니 오늘 드디어 내 힘으로 풀 수가 있었다.

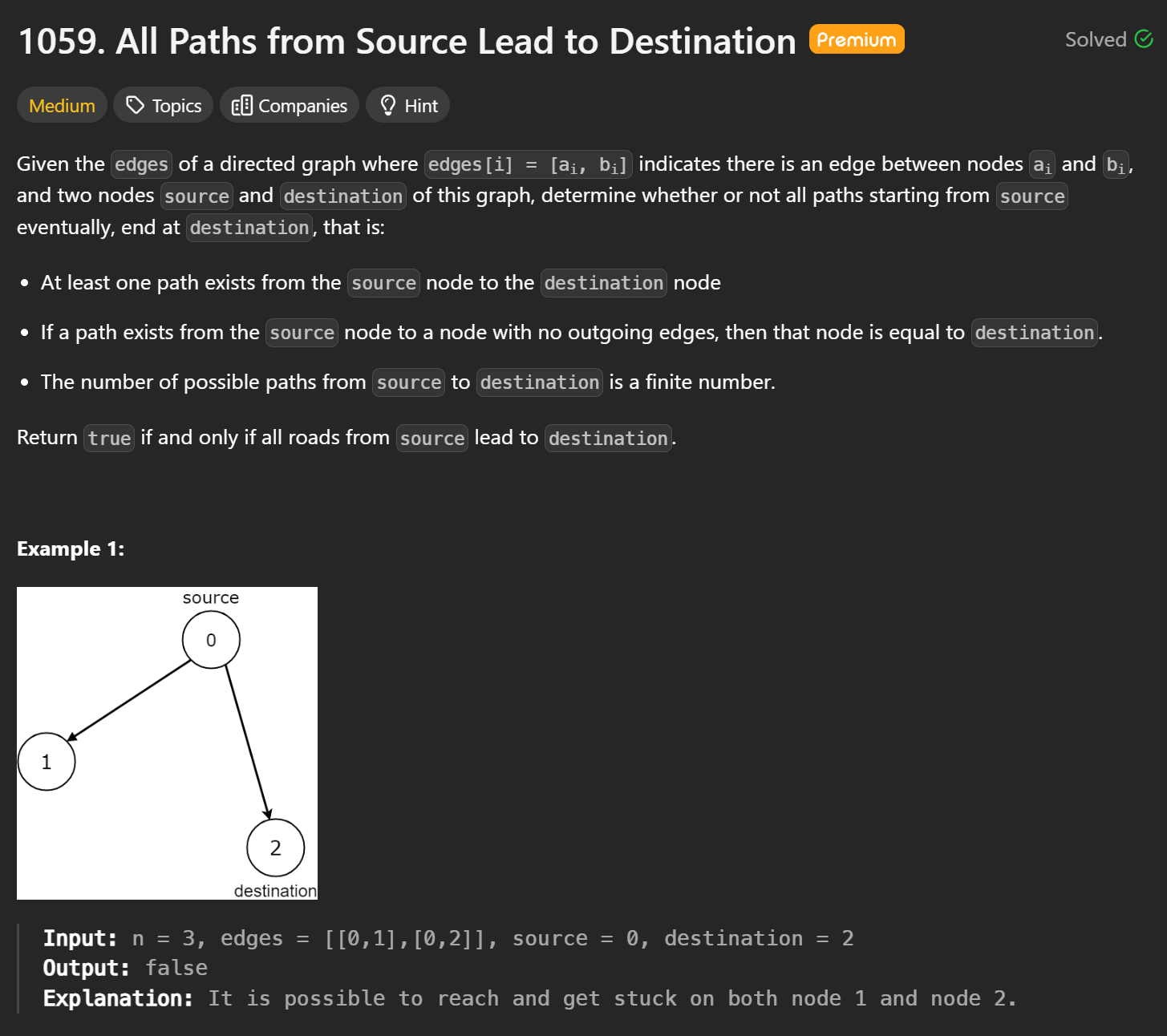
이 문제는 destination 으로 향하는 모든 노드의 path 가 존재하는지를 물어보는 문제였다.

destination 으로 가는 path 가 하나라도 존재할 시, 다른 모든 node도 path 가 존재해야 한다는 뜻이다.

이 과정에서, 만약에 중간에 cycle 이 나오거나 아니면 leaf 노드에서 destination이 아닌 노드에 있게 되면은 false 가 반환되야 한다.

Toplogical Sort 에서의 cycle detection 은 back edge 가 존재 하는지의 유무로 알 수 있다. 만약 내가 탐색 중인 노드가 한번 더 방문이 됐다하면은 cycle 이기 때문에 false 를, leaf 노드에 왔는데도 destination 이 아니면 falase 를 반환 해줬다.

class Solution {
public:
    int visited[10001]; 
    bool dfs(vector<vector<int>>& adj, int source, int destination){
        if(visited[source] == 2) return true; 
        if(visited[source] == 1) return false; 
        visited[source] = 1; 
        for(int next : adj[source]){
            if(!dfs(adj,next,destination)) return false; 
        }
        visited[source] = 2; 
        if(adj[source].empty() && source != destination) return false; 
        return true; 
    }
    bool leadsToDestination(int n, vector<vector<int>>& edges, int source, int destination) {
        vector<vector<int>> adj(n); 
        for(vector<int>& v : edges){
            int from = v[0], to = v[1]; 
            adj[from].push_back(to); 
        }

        bool res = dfs(adj,source,destination); 
        return res; 
    }
};