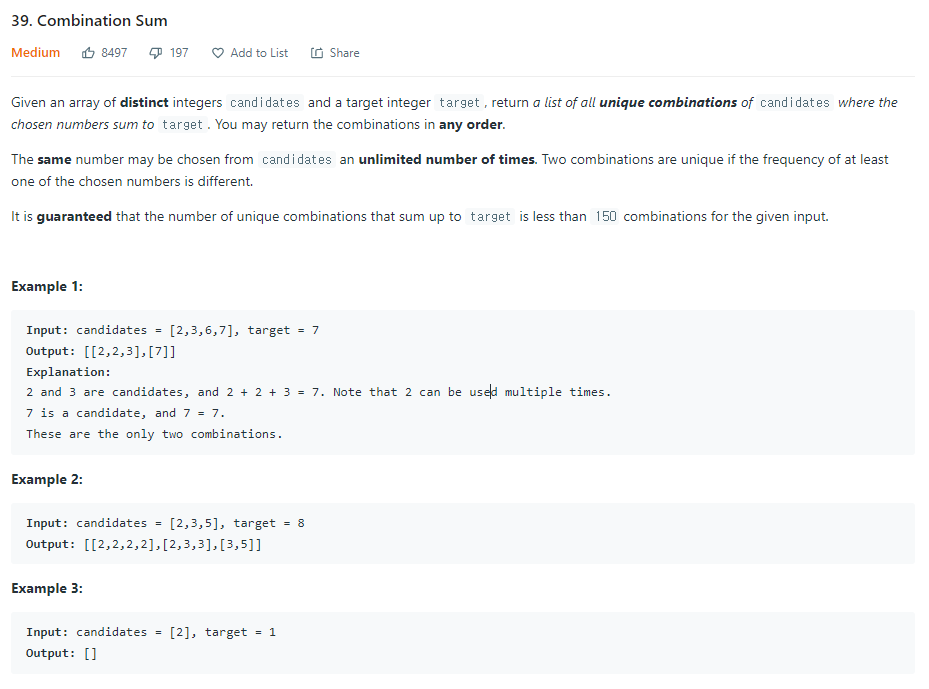
최근 가장 관심을 가지고 풀고있는 backtracking 문제이다. Subsets문제에서 자신감을 얻고 과감하게 도전 해봤지만 문제를 봤을때 어디서부터 시작해야할지 뇌정지가 와서 어버버 하다가 결국 예전에 풀었던 답과 다른사람의 풀이를 보고 나만의 코드로 다시 재해석 했다. Candidates 라는 벡터안에서 한 요소를 여러번 사용할수있다는 가정하에 타겟넘버에 도달할수있는 요소들의 유니크한 조합을 리턴해야하는 문제이다.
내가 멘붕이 왔던점 몇가지는 그냥 단순 for loop 을 이용한 backtracking 을 쓰게되면 어떻게 같은 요소를 여러번 쓰면서 타겟넘버에 도달할수있을까? 라는 안일한 생각이였는데 그냥 내가 backtracking원리를 잘 몰라서 나온 헛소리였다. 그래도 시도는 좋은법이기에 멋있게 시도해봤지만 역시 틀렸다.
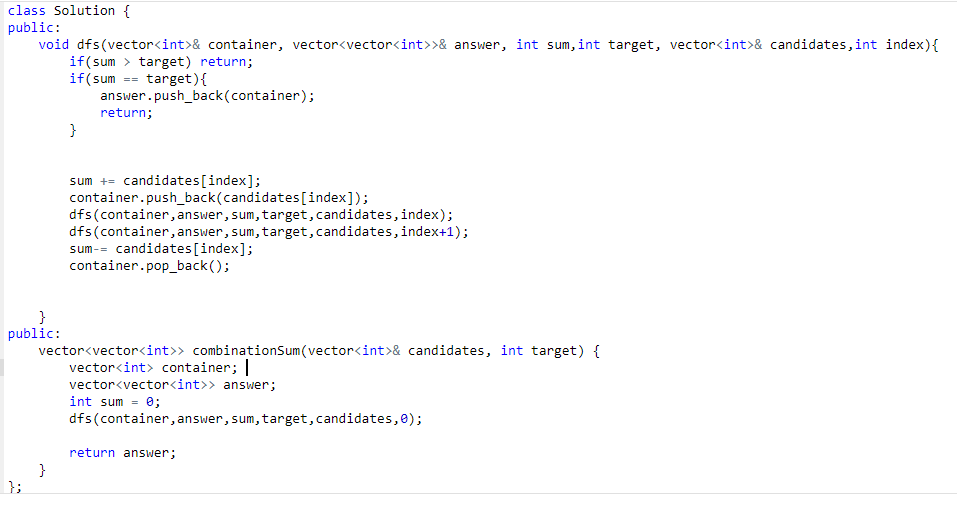
완전히 틀린 코드. 그래도시도는 좋았다고 생각하는 코드이다. 나는 dfs를 두번쓰게되면 뭐라도 나오지 않을까 싶었지만 말도안되는 소리였다. 아예 backtracking 의 원리를 이해 못한꼴.
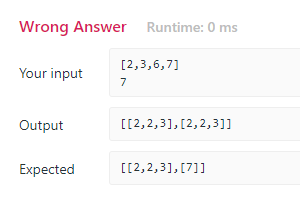
결국 벡터의 끝에도 못가고 그냥 2 하고 3만 주구장창 탐색한 샘이다. 이건 내 이해의 부족이었다고 생각하고 다른 사람의 풀이를 여러번 보고 풀어본 결과 드디어 답이 나왔다.
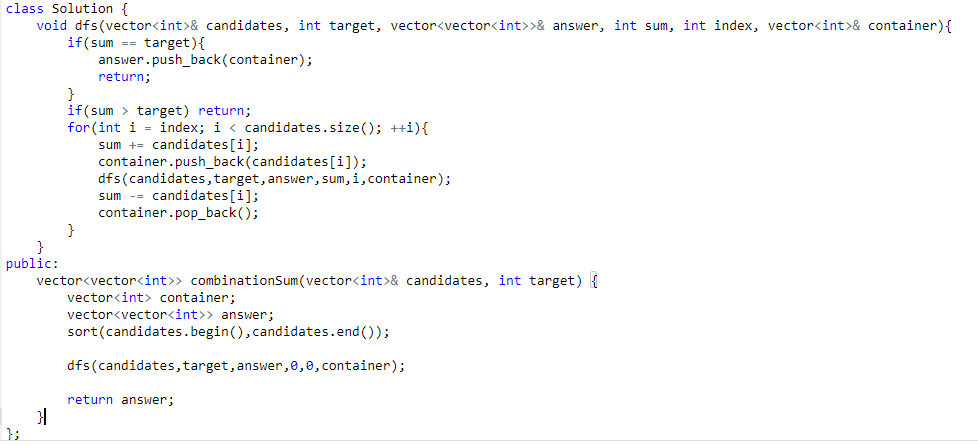
그렇다. 벡터를 끝까지 읽고 테스트 케이스를 전부검색하기 위해서는 for loop을 써야했었고 조합특성상 중복을 피하기 위해 i를 index값으로 설정하면됐었다. 그리고 이전에 있었던 Subsets 문제와는 달리 내가 dfs 콜을 할때 i+1 을 안해준건 같은 요소를 여러번 써야하는 조건이 있었기때문이다 계속 sum을 따라가주고 만약 sum이 타겟보다 크다면 리턴하고 같다면 답에 넣어주면 됐었다. 돌아오는 과정에서 pop_back() 이 되고 sum에서 마이너스 되고 재귀 콜이 끝난 순간부터 벡터의 끝까지 계산하기때문에 이게 맞는 답이었다. 보람을 느낀 문제였다.
배운점:
1. 혼자서 끙끙 될바에 빠르게 답을보고 내꺼로 만들자
2. 재귀를 사용할때는 계속 생각해보고 전에 풀었던 문제도 생각하면서 풀어보자.
