Maximum Length of Subarray With Positive Product

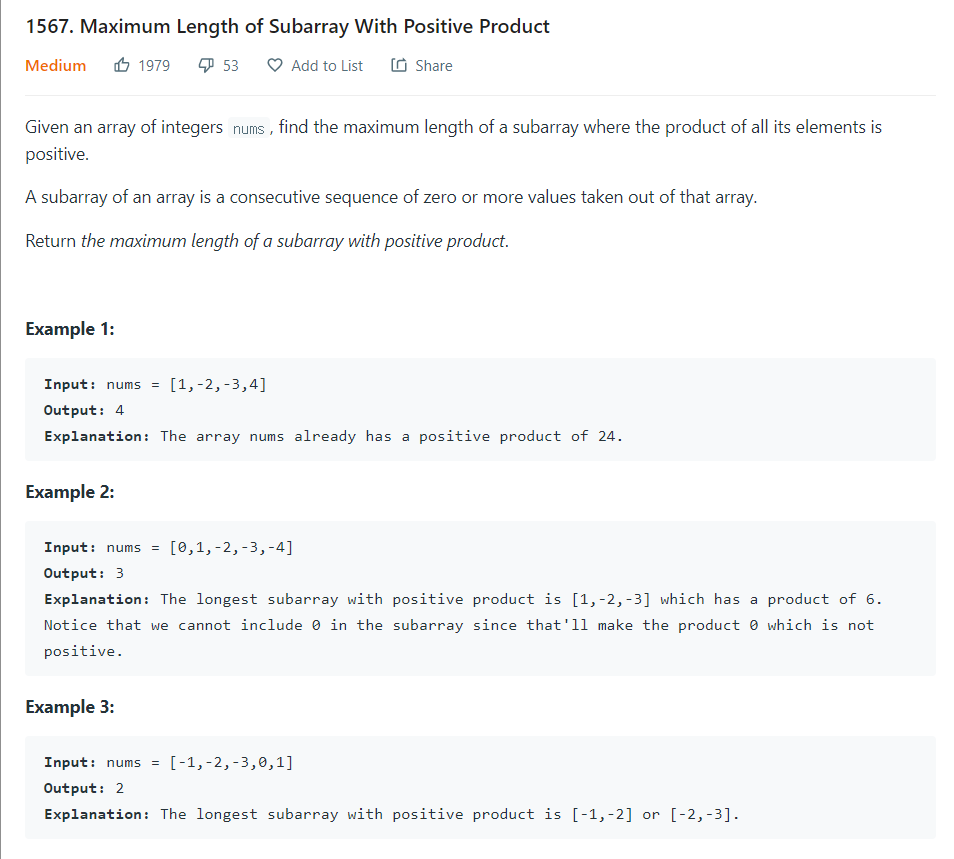
솔직히 계속 풀었던 DP문제 유형중에서도 가장 어려웠다고 느꼈다. 그래서 답을 참고했는데 다른사람들은 DP 방식으로 푼다기 보다 좀 더 Greedy하게 푸는 방향으로 풀어서 내가 원하는 풀이 방식을 계속 찾다가 이번 풀이가 가장 괜찮아 보였다. 이 풀이를 보고도 이해하느라 꽤 애먹었고 내가 직접 작성하면서 겨우 이해했다.

이번에 처음으로 DP를 2D 방식으로 설계했다. 그리고 특이하게 첫번째 [] 에는 Positive 값을 저장하는 이유로 사용하고 두번째 [] 에는 Negative 값을 저장하는 용도로 사용되었다. 마치 배열 문제를 풀때 x와 y의 값을 저장하는 것처럼 사용했는데 이유가 있었다. 이 문제는 가장 긴 Subarray 를 구해야 하는데 그 안에 값들이 전부 Positive 여야 한다. 그렇기 때문에 별 생각 없이 모든 값들을 DP테이블에 중첩시켜서 저장시키면은 답을 절대 구할 수 없다.

이 문제의 핵심으로 2가지만 이해하면 된다.

1. 만약 현재 값이 Positive면은 바로 전 단계에서의 Positive 최대값에 +1을 하면 된다 (왜냐? Positive * Positive 는 항상 Positive 이기때문)

2. 만약 현재 값이 Negative면은 바로 전 단계에서의 Negative 최대값을 보고 Positive 최대값에 +1을 해주면 된다. (왜냐? Negative * Negative = Positive 이기때문)

다만, 1하고 2에서 조심해야 하는 부분은 있다. 1에서 Positive 최대값에 +1을 해주고 난 후에 만약 바로 전 단계에서 Negative 값이 있다면 Negative 최대값도 업데이트 해줘야한다. 왜냐면은 Positive * Negative = Negative 이기 때문에 dp[i][1]은 전 단계의 최대 Negative 값 +1을 해줘야한다.

2에 경우 Negative Negative 로 인해 Positive를 업데이트 해주고 난 후에는 바로 전 단계의 Positive 값에서 +1 을 해줘야한다 왜냐면은 Positive Negative = Negative 이기때문. 결국 포인트는 dp[x][0] 에는 Positive의 최대값만, 그리고 dp[x][1]에는 Negative의 최대값만 가지고 있는 것이다.

class Solution {
    public int getMaxLen(int[] nums) {
        int[][] dp = new int[nums.length][2]; 
        if(nums[0] > 0) dp[0][0]++; 
        if(nums[0] < 0) dp[0][1]++; 
        
        int answer = dp[0][0]; 
        
        for(int i = 1; i < nums.length; i++){
            if(nums[i] != 0){
                if(nums[i] > 0){
                    dp[i][0] = dp[i-1][0] + 1; 
                    if(dp[i-1][1] > 0) dp[i][1] = 1+dp[i-1][1];
                }
                else{
                    if(dp[i-1][1] > 0) dp[i][0] = dp[i-1][1] + 1; 
                    dp[i][1] = dp[i-1][0] + 1; 
                }
            }
            answer = Math.max(answer,dp[i][0]); 
        }
        
        return answer; 
    }
}