Number of Operations to Make Network Connected (JAVA)

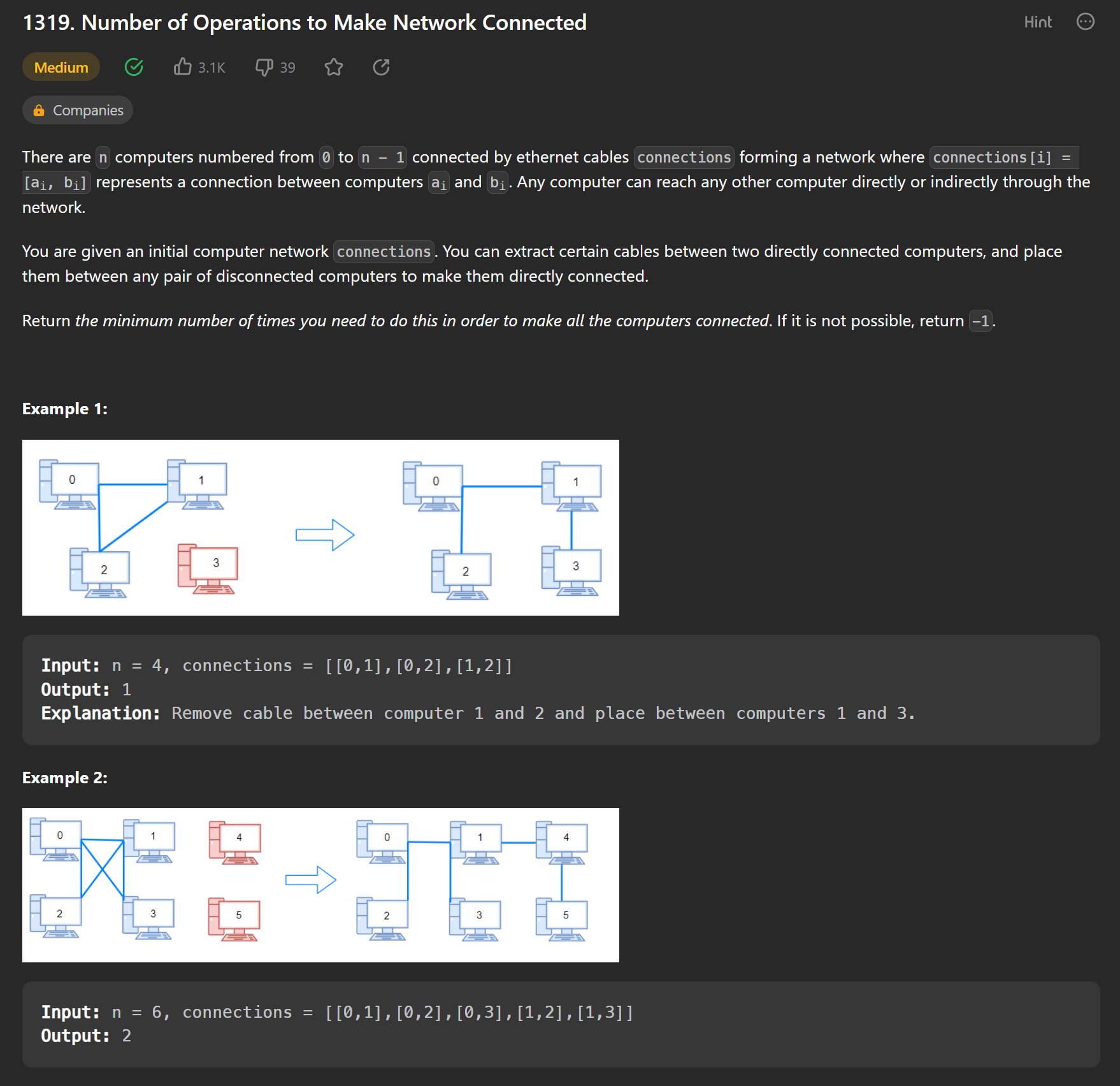
예전에 군대를 전역하고 풀었던 문제를 다시 도전해봤다. 그렇게 어려운 문제는 아니고 그냥 모둔 connected 그래프를 탐색해주고 연결이 되지 않은 그래프의 숫자를 가지고 오는 문제다. 이 문제를 어렵지 않게 풀었음에도 이렇게 다시 올리는 이유는 자바로 풀이를 했을때 같은 코드여도 TLE가 걸린 풀이와 걸리지 않은 풀이가 있어서 기록하고 싶었다.

보통 그래프 문제를 만들때는 adj 그래프라고 내가 임의로 그래프를 0번부터 N번까지 만들어야 하는 경우가 있는데 C++에서는 정말로 벡터를 만드는게 쉬워서 아무 문제 없이 했지만 자바에서 2D List 를 만드는거는 조금 더 많은 작업이 필요하다.

아래에 코드는 같은 로직에도 TLE가 걸린 코드고 잘 살펴보면은 adj 그래프에 계속해서 .add를 불러주고 있다. 그리고 2D List를 만들때 아래와 같이 List<List<... 형식으로 접근하는거는 생각보다 많은 시간이 걸리는거같다.

class Solution {
    int answer; 
    public void dfs(int node, List<List<Integer>> adj, boolean[] visited){
        
        visited[node] = true; 
        for(int paths : adj.get(node)){
            if(!visited[paths]){
                visited[paths] = true; 
                answer--; 
                dfs(paths,adj,visited); 
            }
        }
    }
    public int makeConnected(int n, int[][] connections) {
        if(connections.length < n-1) return -1; 
        List<List<Integer>> adj = new LinkedList<List<Integer>>();
        boolean[] visited = new boolean[n]; 
        answer = n-1; 
        for(int i = 0; i < n; i++){
            adj.add(new LinkedList<Integer>()); 
        }
        for(int[] path : connections){
            adj.get(path[0]).add(path[1]); 
            adj.get(path[1]).add(path[0]); 
        }
        
        for(int i = 0; i < n; i++){
            //dfs(i,adj,visited); 
            if(visited[i] == false){
                //System.out.println(i); 
                dfs(i,adj,visited); 
            }
        }
        
       
        return answer;  
    }

다른 사람의 풀이를 봤을때 생각보다 더 깔끔하다고 느껴서 기록하고 싶었다. 내가 딱 원했던 풀이고 앞으로 임의에 그래프를 만들 경우가 생길때 이 그래프를 참고해서 만들 생각이다. List<인터져>[] graph 로 만든 후에 각 index마다 ArrayList<>()를 배정해준게 되게 인상깊게 보이고 앞으로 좀 참고해야겠다.

class Solution {
    int answer; 
    public int makeConnected(int n, int[][] connections) {
        if (connections.length < n - 1) return -1; // To connect all nodes need at least n-1 edges
        List<Integer>[] graph = new List[n];
        for (int i = 0; i < n; i++) graph[i] = new ArrayList<>();
        for (int[] c : connections) {
            graph[c[0]].add(c[1]);
            graph[c[1]].add(c[0]);
        }
        //int components = 0;
        answer = n - 1; 
        boolean[] visited = new boolean[n];
        for (int v = 0; v < n; v++) dfs(v, graph, visited);
        return answer; // Need (components-1) cables to connect components together
    }
    void dfs(int u, List<Integer>[] graph, boolean[] visited) {

        visited[u] = true;
        for (int v : graph[u]){
            if(!visited[v]){
                dfs(v, graph, visited);
                answer--; 
            }
        }
    }
}