6. 확률론

유승우·2022년 5월 4일

딥러닝은 확률론 기반의 기계학습 이론에 바탕을 두고 있으며, 손실함수들의 작동원리는 데이터 공간을 통계적으로 해석해서 유도하기 때문에 분산 및 불확실성을 최소화하기 위해서는 확률론의 이해가 필요하다.

확률분포(probability distribution)

실제 데이터만 가지고 확률분포를 추론할 수 없기 때문에, 기계학습 방법을 통해 확률 분포를 추론한다.
데이터 공간에 정답 레이블이 있으면 $\chi$ x y 라 표기하고, 정답 레이블이 없다면 $\chi$ 으로 표기한다
확률변수
- 데이터 공간 상에서 관측 가능한 데이터들을 확률 변수라 한다
- 확률 변수는 함수로 이해하게 되는데 데이터를 추출할 때 이 확률 변수를 이용해 추출한다.
  
  ex ) 실수로 구성되어있는 데이터 공간에서 두 개의 데이터만 뽑는 확률 변수가 있으면 그것은 이산확률변수

이산확률변수 vs 연속확률변수

이산확률변수

\mathbb{P\mathbf{(X\in A)}} = \sum_{x\in A}P(X = x)

연속확률변수

\mathbb{P\mathbf{(X\in A)}} = \int_{A}P(x)dx

P(x)=\displaystyle \lim_{h \to 0}\frac{\mathbb{P}(x-h \leq X\leq x+h)}{2h}

결합 분포(Join distribution)

전체 데이터 X 와 Y가 주어져 있을 때의 분포를 결합 분포라 하며, 이를 통해 확률 분포를 모델링 할 수 있다
원래 확률 분포와 상관없이 결합 분포를 사용할 수 있으며, 원래 데이터의 확률 분포를 추출하는 D와 주어진 데이터에서 실증적으로 분포를 추정하는 분포는 다를 수 있다.
컴퓨터를 가지고 데이터를 분석하기 때문에 원래 확률 변수 분포 D와 다르다 할지라도 거기에 근사할 수 있는 방법을 알 수 있기 때문에, 주어진 데이터의 모양을 보고 적절하게 선택을 할 수 있다.

주변 확률 분포

X에 대한 주변확률 분포는 각각의 입력 X에 대해 y에 해당하는 것을 더해주거나 적분으로 유도할 수 있다. 또한, y에 대한 주변 확률 분포도 구할 수 있는데, 입력 X를 더해주거나 적분하는 것으로 얻을 수 있다.
아래의 히스토그램은 y값에 상관없이 x에 해당하는 점들의 빈도 수를 합하여 주변확률분포를 나타냈다.

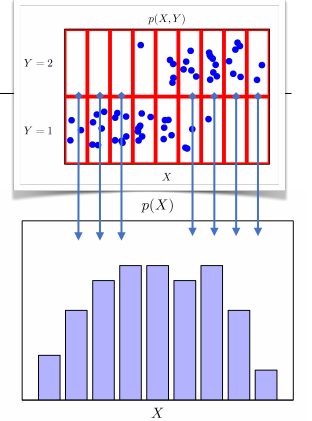
조건부 확률 분포

두 입력과 출력 사이의 통계적 관계를 모델링하거나 예측 모형을 세울 때 사용을 할 수 있다
주어진 class에 대해서 X의 분포가 어떻게 되어있는지 알고 싶을 때는 주변 확률 분포 보다는 조건부 확률 분포를 사용하는 것이 더 명확하게 알 수 있다.

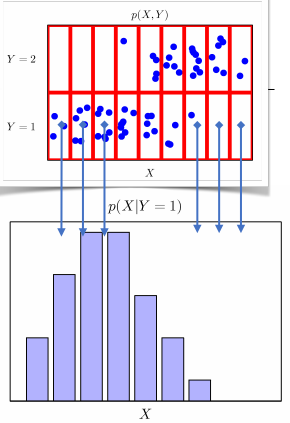
조건부확률
- $P(y|X)$ 는 입력변수 x에 대해 정답이 y일 확률을 의미하며, 연속형일 경우에는 확률 대신 밀도를 사용
- 분류 문제의 경우 로지스틱 회귀에서 사용했던 선형모델과 소프트맥스 함수의 결합으로 데이터에서 추출된 패턴을 기반으로 확률을 해석하는데 사용된다
- 회귀 문제의 경우 조건부기대값 $E[y|x]$ 을 추론하는데, L2-norm을 최소화 하는 함수와 일치한다는 증명이 되어 있기 때문에 사용한다

E_{y \sim P(y|x)}[y|x] = \int_{y}yP(y|x)dy

기대값

기대값은 데이터를 대표하는 통계량이면서 여러 통계적 범함수를 계산할 수 있다.
연속확률분포의 경우 주어진 함수에 확률밀도함수를 곱한 다음 적분을 하고, 이산확률분포의 경우 주어진 함수에 확률질량함수를 곱한 다음 급수를 취해 준다.

E_{x \sim P(x)}[f(x)] = \int_{x}fxP(x)dy , \\E_{x \sim P(x)}[f(x)] = \sum_{x\epsilon \chi }f(x)P(x)

V(x) = E_{x\sim P(x)}[(x-E[x])^2]

Skewness(x) = E\left [ \left ( \frac{x-E[x]}{\sqrt{V(x)}}^3 \right ) \right ]

Cov(x_1,x_2) = E_{x_1,x_2\sim P(x_1,x_2)}[(x_1 - E[x_1])](x_2-E[x_2])

몬테카를로 샘플링

기계학습의 많은 문제들은 확률분포를 명시적으로 모를 때가 대부분이고, 이 때 몬테카를로 샘플링 방법을 사용한다.
확률분포를 모를 때, 샘플링 하는 법을 알고 있다면, 적분이나 합 대신 샘플링을 통해 추출된 데이터들에 대해 산술평균을 취해주면 기대값에 근사한 값을 구할 수 있다
몬테카를로 샘플링은 독립추출만 보장된다면 대수의 법칙에 의해 수렴성을 보장한다.

E_{x\sim P(x)}[F(x)] \approx \frac{1}{N}\sum_{i=1}^{N}f(x^{(i)}) , x^{(i)}\sim ^{i.i.d} P(x)

몬테카를로 예제 : 적분 계산하기