1. 개념
- 배열을 앞부분과 뒷부분으로 나누어 각각 정렬한 후 병합하는 작업을 반복하여 정렬을 수행하는 알고리즘
- 전형적인 분할 정복 방법이 적용된 알고리즘
2. 과정
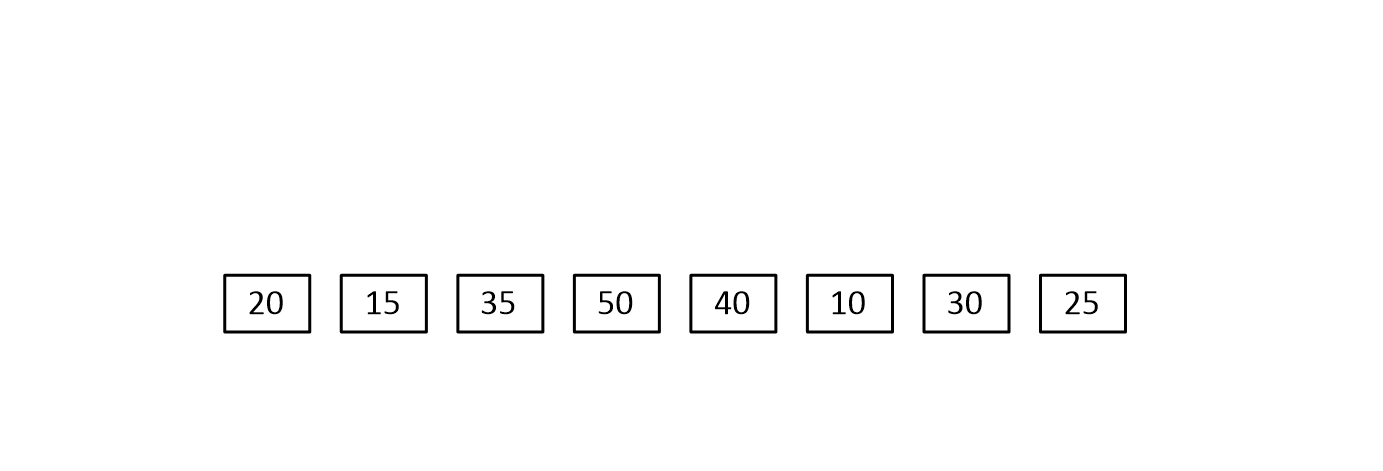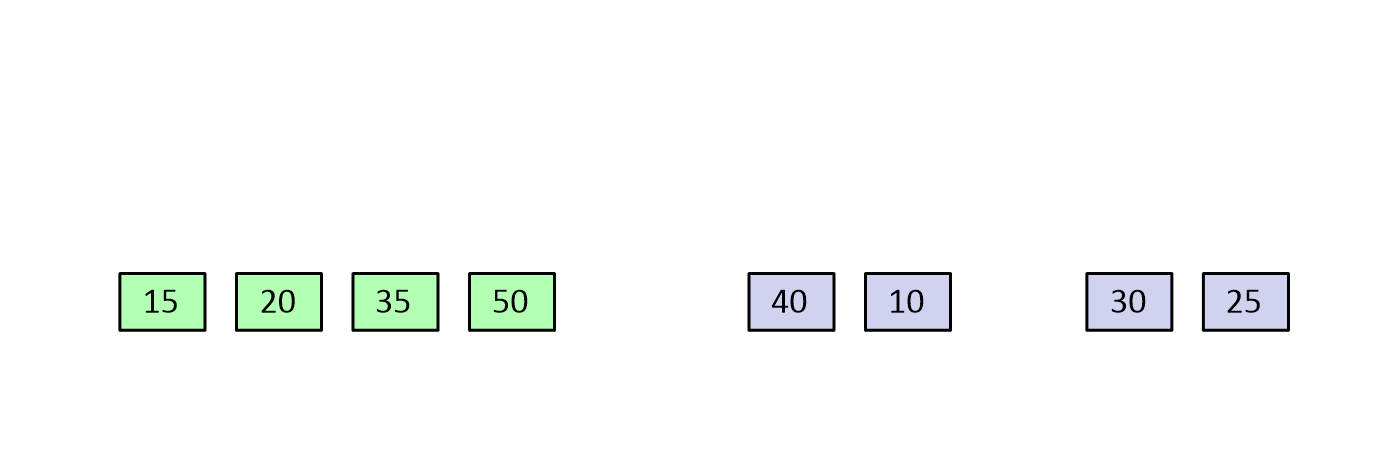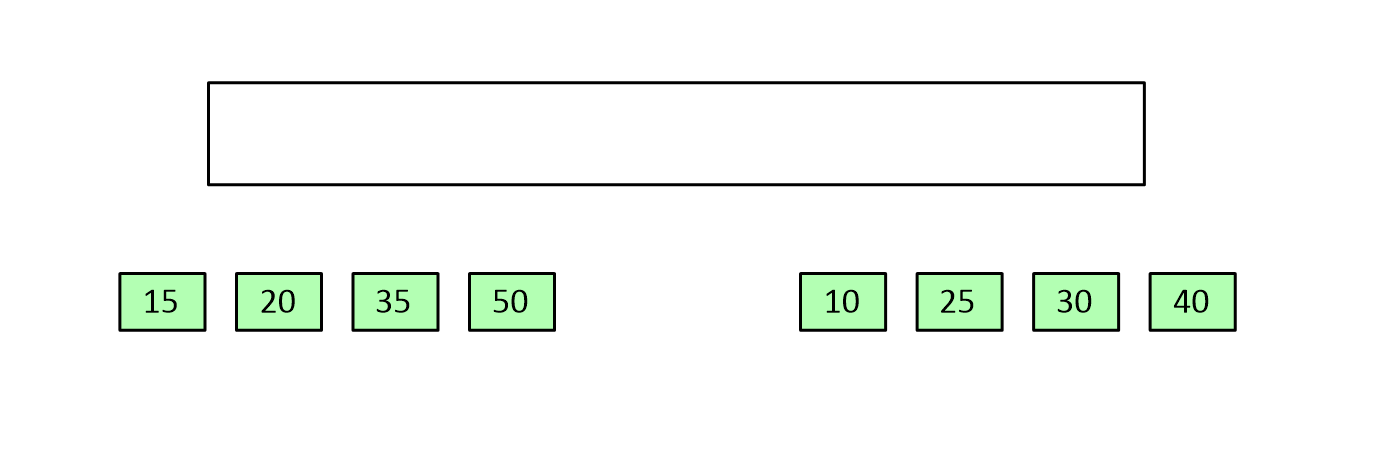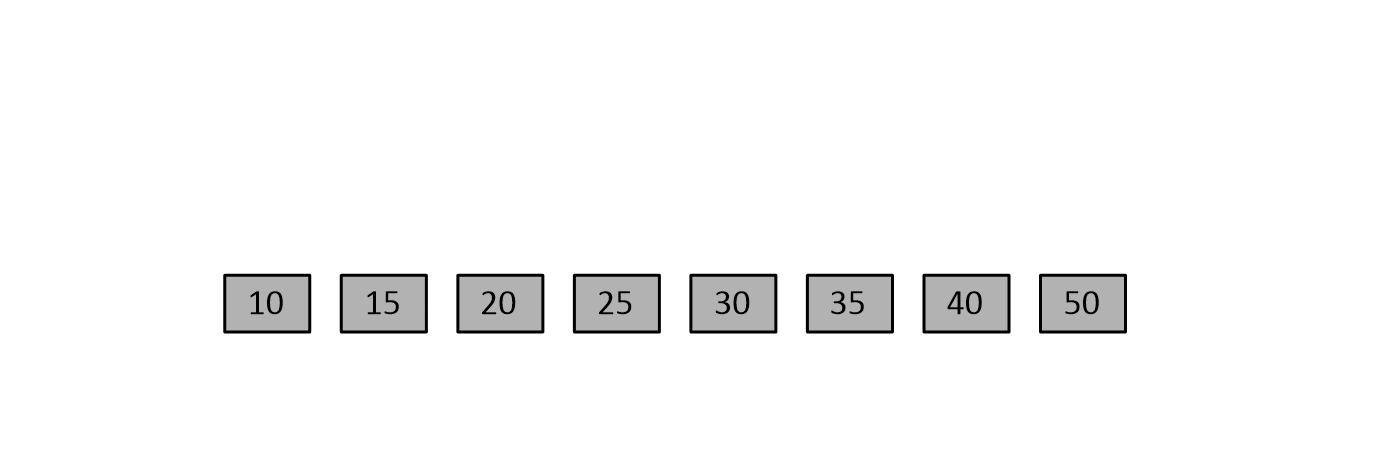
- 분할 : 배열을 동일한 크기의 두 개의 부분배열(n/2)로 분할한다.
- 정복 : 각각의 부분배열에 대해 합병 정렬을 순환적으로 적용하여 두 부분배열을 정렬한다.
- 결합 : 정렬된 두 부분배열을 합병하여 하나의 정렬된 배열을 만든다.
3. 구현
/* n: 배열의 길이 */
public class MergeSort {
static int[] buff; // 1. 작업용 배열
static void mergeSort(int[] arr, int n) {
buff = new int[n];
divideAndMerge(arr, 0, n-1); // 2. 배열 전체 병합 및 정렬
buff = null; // 7. 작업용 배열 해제
}
static void divideAndMerge(int[] arr, int start, int end) {
// 부분배열의 길이가 1이 아닌 경우
if (start < end) { // 3.
int mid = (start + end) / 2; // 3-1.
// 3-2.
divideAndMerge(arr, start, mid); // 왼쪽 부분배열 분할
divideAndMerge(arr, mid + 1, end); // 오른쪽 부분배열 분할
merge(arr, start, mid, end); // 3-3. 배열 병합 정렬
}
}
static void merge(int[] arr, int start, int mid, int end) {
// 4. 작업용 배열에 왼쪽 부분배열 복사
int leftArrIdx;
int leftArrToBuffIdx = 0;
for(leftArrIdx = start; leftArrIdx <= mid; leftArrIdx++) {
buff[leftArrToBuffIdx++] = arr[leftArrIdx];
}
// 5. 작업용 배열에 오른쪽 부분배열 복사
int rightArrIdx = start;
int rightArrToBuffIdx = 0;
while(leftArrIdx <= end && rightArrToBuffIdx < leftArrToBuffIdx) {
arr[rightArrIdx++] = (buff[rightArrToBuffIdx] <= arr[leftArrIdx]) ?
buff[rightArrToBuffIdx++] : arr[leftArrIdx++];
}
// 6. 작업용 배열에 남은 데이터를 원본 배열에 복사
while(rightArrToBuffIdx < leftArrToBuffIdx) {
arr[rightArrIdx++] = buff[rightArrToBuffIdx++];
}
}1. 병합한 결과를 일시적으로 저장할 작업용 배열 buff를 생성한다.
2. 실제로 정렬 작업을 수행할 divideAndMerge 메서드를 호출한다.
3. 부분 배열의 길이가 1이 아닌 경우(start < end), 분할-정렬- 병합을 수행한다. start = end라면, 부분 배열에 요소가 1개만 있는 상태로 배열 분할 및 정렬이 필요 없다.
3-1. 병합 정렬은 늘 동일한 크기로 배열을 분할하므로, 배열의 중간 위치를 피벗(mid)으로 지정한다.
3-2. 피벗을 기준으로 배열을 왼쪽(arr[start] ~ arr[mid], 피벗 포함)과 오른쪽(arr[mid+1] ~ arr[end])으로 나누어 분할한다.
3-3. 왼쪽 부분배열과 오른쪽 부분배열이 모두 분할하여 정렬된 상태라면 배열 전체를 병합 및 정렬하기 위해 merge 메서드를 호출한다.
4. 작업용 배열에 왼쪽 부분배열의 값들을 복사한다. 모든 값이 복사되면 버퍼의 커서(rightArrToBuffIdx)가 왼쪽 부분배열의 마지막 요소의 다음 위치와 동일한 위치에 오게된다. 즉, 작업용 배열의 커서는 mid+1에 위치한다.
5. 왼쪽 부분배열과 오른쪽 부분배열의 값 중 작은 값을 원본 배열에 복사한다. 이 작업을 오른쪽 부분배열의 커서가 마지막 위치를 벗어나기 전까지 반복한다.(rightArrToBuffIdx < leftArrToBuffIdx) 복사가 완료되면 작업용 배열의 커서가 오른쪽 부분배열의 길이만큼 이동된 상태가 된다.
6. 4.와 5.를 수행한 후 작업용 배열에 남은 데이터가 있다면 원본 배열에 값을 모두 복사한다.
7. 모든 작업이 완료되면 작업용 배열을 해제해준다.
4. 성능 분석
4-1. 병합 함수(merge()) 수행 시간
- 왼쪽 부분배열의 크기 : n/2
- 오른쪽 부분배열의 크기 : n/2
- 두 부분배열 간 비교횟수
n/2 ~ ((n/2) + (n/2) - 1 = n-1) → 최악
∴ Θ(n)
4-2. 병합 정렬(divideAndMerge()) 수행 시간
static void divideAndMerge(int[] arr, int start, int end) { // T(n)
if (start < end) {
int mid = (start + end) / 2;
divideAndMerge(arr, start, mid); // T(⌊n/2⌋)
divideAndMerge(arr, mid + 1, end); // T(⌊n/2⌋)
merge(arr, start, mid, end); // Θ(n)
}
}T(n) = T(⌊n/2⌋) + T(⌊n/2⌋) + Θ(n) (n>1), T(1) = 1
T(n) = 2T(⌊n/2⌋) + Θ(n)
∴ T(n) = O(nlogn)
5. 특징
- 분할 정복 알고리즘이다.
- 안정적 정렬 알고리즘이다.
- 작업용 배열이 필요하므로 제자리 정렬 알고리즘이 아니다.
- 여기서는 작업용 배열로
buff가 사용됨
- 여기서는 작업용 배열로
- 최선/최악/평균 수행 시간이 모두 O(nlogn)이다.
📖 참고
- Bohyoh Shibata. (2020). Do it! 자료구조와 함께 배우는 알고리즘 입문 - 자바편(강민 옮김). 이지스퍼블리싱
- 이관용. "알고리즘 4강. 분할정복 알고리즘 (2)" 방송통신대학교, 2022년.
- 이관용. "알고리즘 11강. 정렬 알고리즘 (2)" 방송통신대학교, 2022년.