Batch Normalization (배치 정규화)
Batch
✅ 일반적인 Gradient Descent
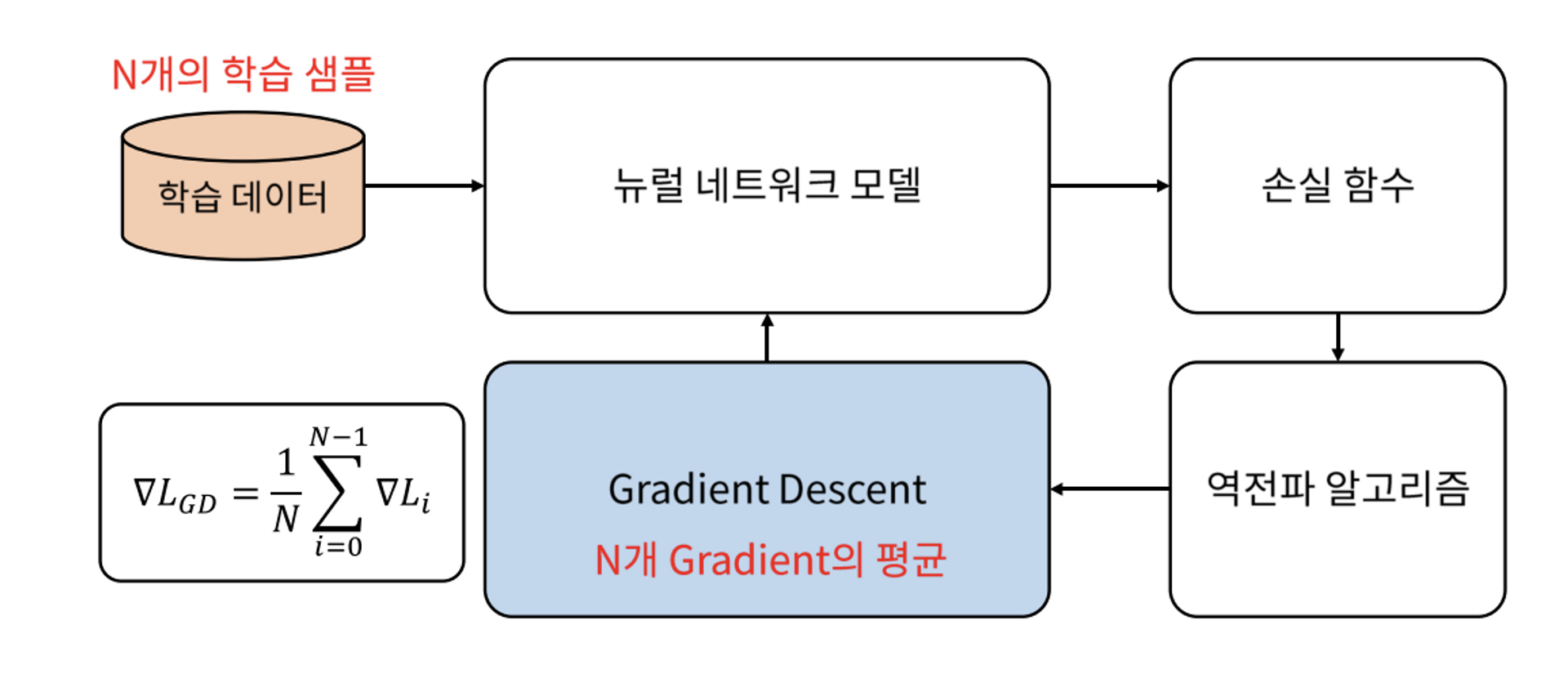
batch를 사용하지 않는 일반적인 gradient descent 방법에서는 gradient를 한 번 업데이트 하기 위해 모든 학습 데이터를 사용해야 한다.
즉, N개의 학습 데이터를 모두 모델에 넣고, 각각의 loss를 구하고, 이를 바탕으로 얻얻어진 N개 gradient의 평균으로 한번에 모델 업데이트를 하는 방식이다.
그러나 이런 방식으로 하면 대용량 데이터를 한 번에 처리하지 못한다는 단점이 있기 때문에 데이터를 batch 단위로 나눠서 학습하는 방법을 일반적으로 사용한다.
따라서, batch는 대용량 데이터의 Gradient Descent를 처리하기 위해 나누는 학습 데이터의 단위라고 할 수 있다.
✅ Stochastic Gradient Descent
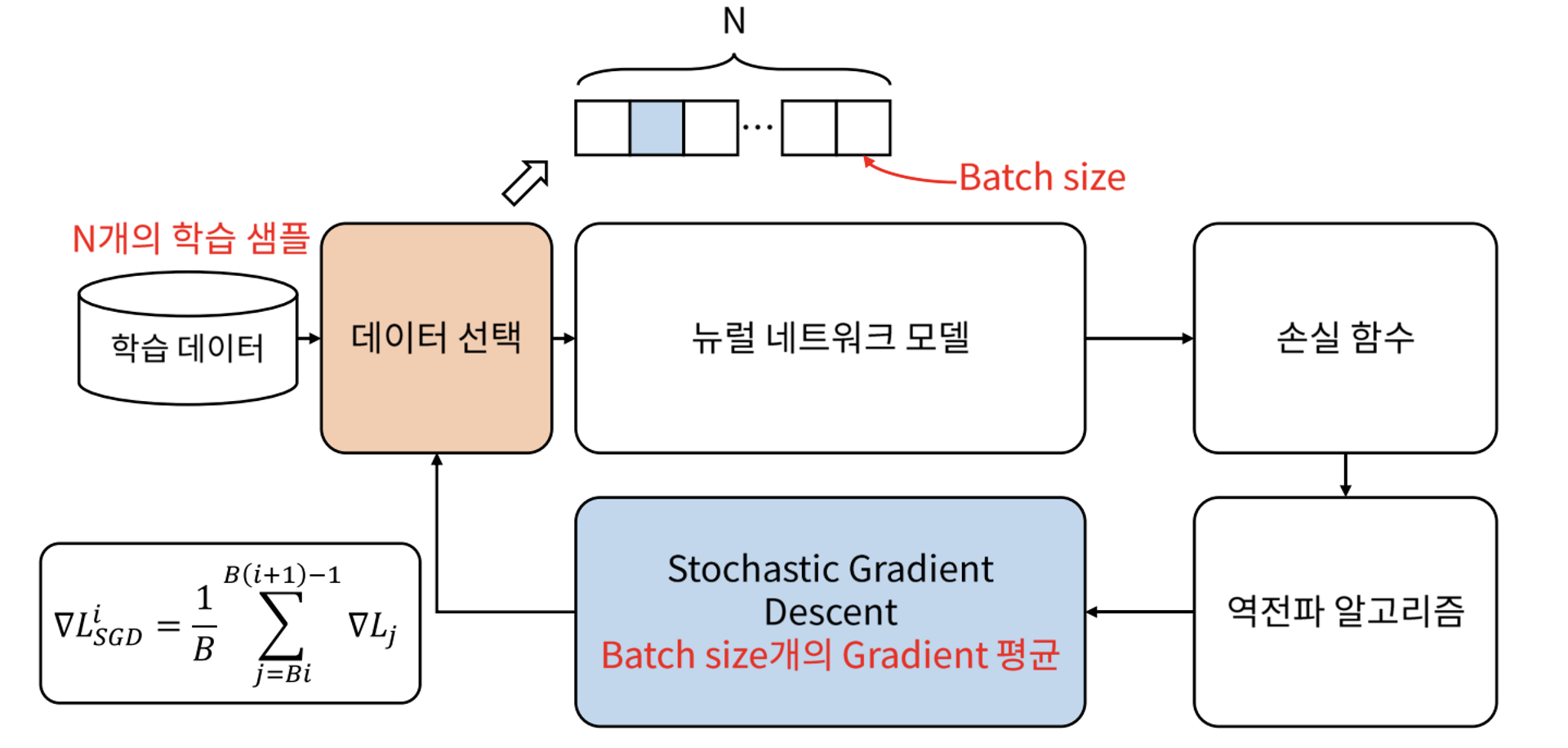
Stachastic Gradient Descent(SGD)에서는 gradient를 한 번 업데이트 하는 데에 batch size 만큼의 데이터를 사용한다.
즉, N개의 학습 데이터 중 batch size B개의 데이터의 loss를 구하고, 이를 통해 얻어진 B개 gradient만의 평균으로 모델을 업데이트하는 작업을 반복하는 방식이다.
batch size가 너무 커지면 batch를 나누는 의미가 없어지고, 너무 작아지면 학습 시간이 과도하게 길어질 수 있다. 따라서 적당한 크기의 batch size를 설정하는 것이 중요하다.
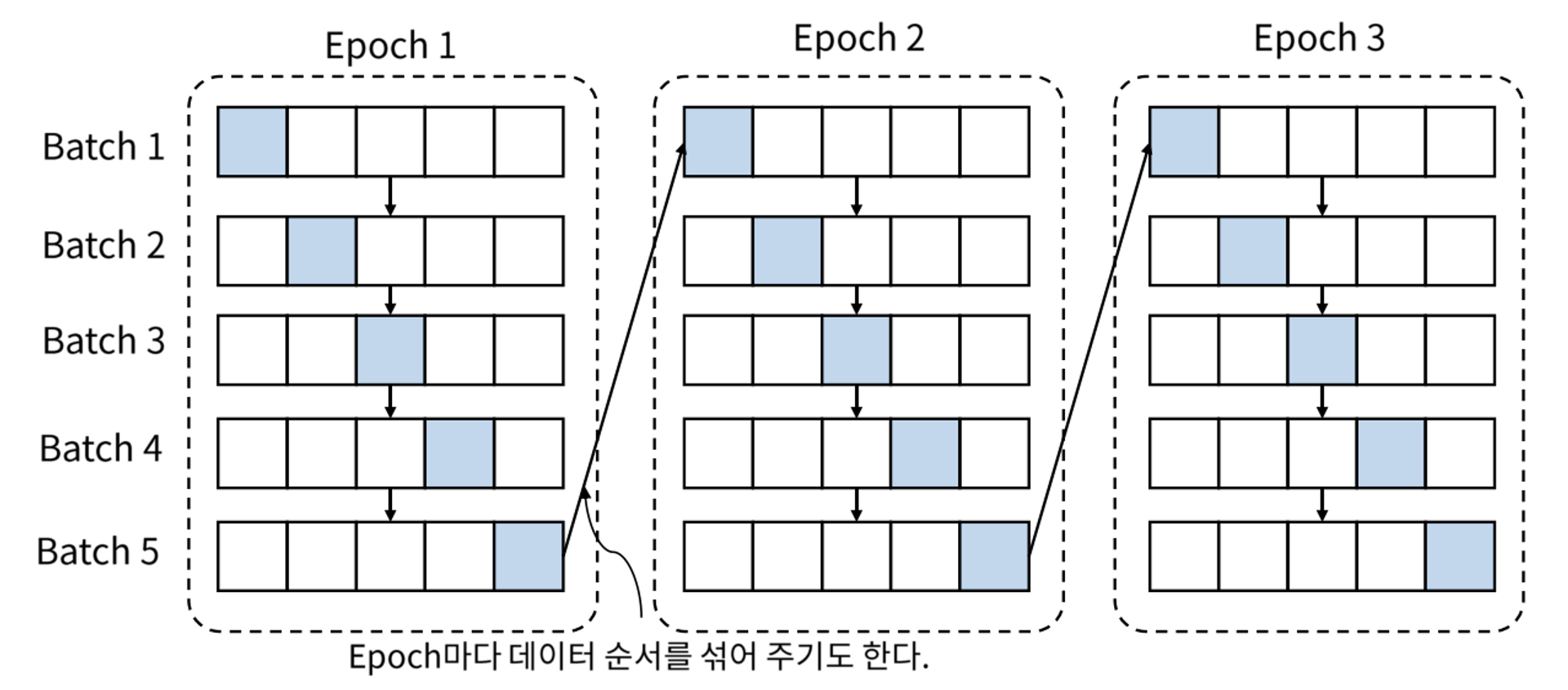
batch를 사용한 학습의 전체적인 흐름
Internal Covariant Shift
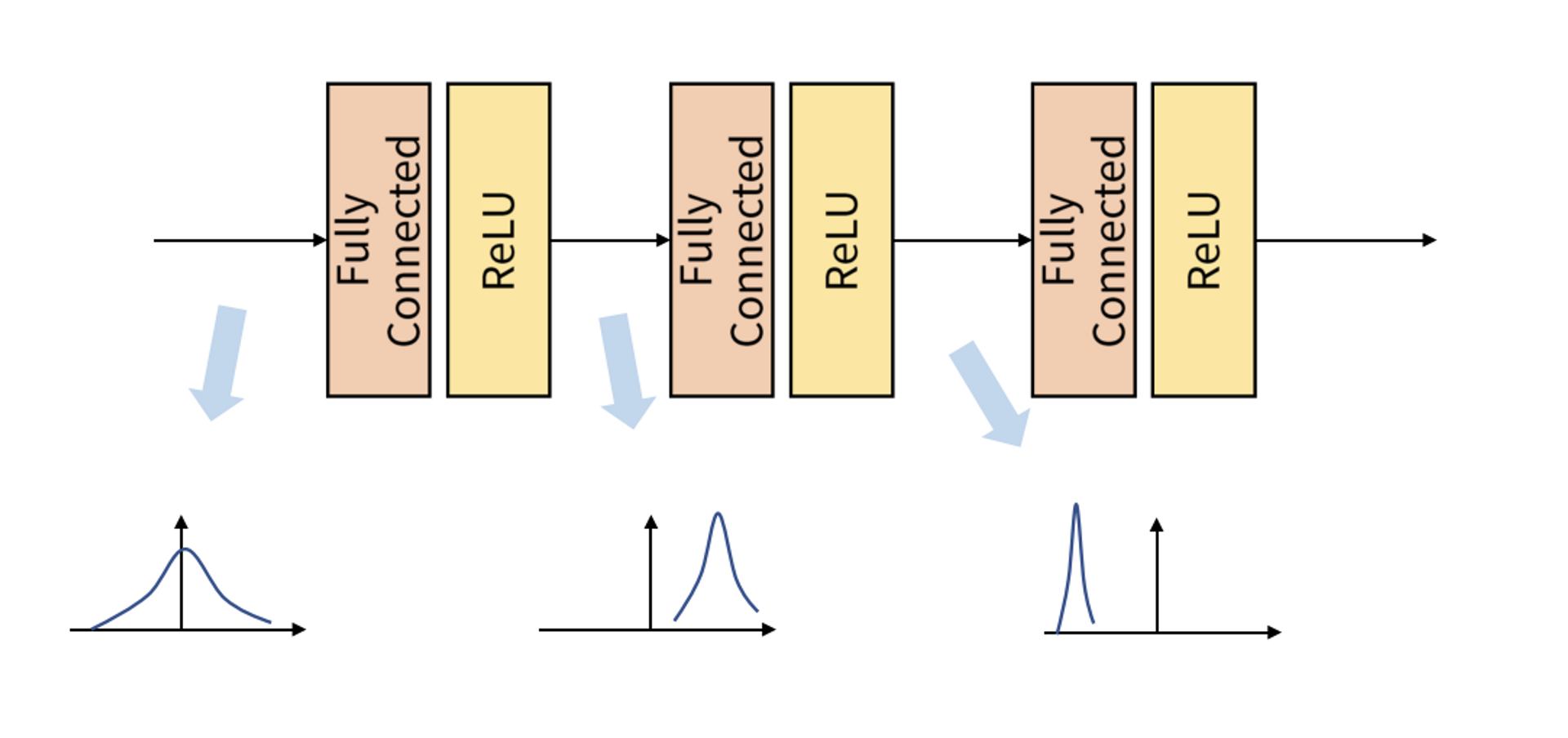
위 그림과 같이 학습 과정에서 layer를 거칠때마다 입력 데이터의 분포가 달라지는 현상을 Internal Covariant Shift라고 한다.
각 layer에서 입력 feature를 받아 convolution이나 fully connected 등의 연산을 거친 뒤 activation function을 적용하는데, 이 과정에서 연산 전/후의 데이터 분포가 달라지는 경우가 있기 때문에 이런 현상이 발생한다.
이와 유사하게 batch 단위로 학습을 진행할 때에도 각 batch 간의 데이터 분포에 차이가 발생할 수 있다.
즉, 각 batch마다 데이터가 상이해지며, 이것이 앞서 말한 Internal Covariant Shift 문제이다.
이 문제를 개선하기 위한 개념이 바로 Batch Normalization이다.
학습 단계의 Batch Normalization

✅ Batch 단위의 정규화
핵심은 각 batch 별로 정규화를 해주어야 한다는 것이다. batch마다 각각의 평균과 분산을 이용해 normalizaton을 적용해야 각 batch들이 표준 정규 분포를 각각 따르게 된다.
학습 단계에서의 batch normalization을 통해 모든 feature를 정규화 해주면 모든 feature가 동일한 scale을 갖게 되어 learning rate를 더 쉽고 효율적으로 결정할 수 있게 된다는 이점이 있다.
만일 각 feature의 scale이 제각각이면, gradient가 달라지며, 같은 learning rate에 대해 weight마다 반응하는 정도가 달라진다. 높은 gradient를 가진 weight에서는 gradient exploding이 발생하고, 낮은 gradient를 가진 weight에서는 gradient vanishin이 발생하는 것이다.
그러나 normalization을 통해 각 feature의 scale을 통일시켜 주면 gradient descent에 따른 weight들의 반응이 같아지기 때문에 학습에 유리해진다.
✅ 파라미터 의 역할
일반적으로 batch normalization은 layer 안에서 activation function 앞에 적용된다. 이 때, 정규화를 거쳐 weight 값의 평균이 0, 분산이 1인 상태로 ReLU function을 적용한다고 가정하면, 절반에 해당하는 y축 왼쪽 부분이 모두 0이 되어버린다. 정규화를 거친 의미가 없어져버리는 것이다.
따라서 를 정규화된 값에 곱하고 더해서 y축 왼쪽 부분이 모두 0이 되어버리지 않게 방지해준다. 물론 이 값들은 학습 과정을 통해 점차 최적의 값을 찾아간다.
추론 단계의 Batch Normalization
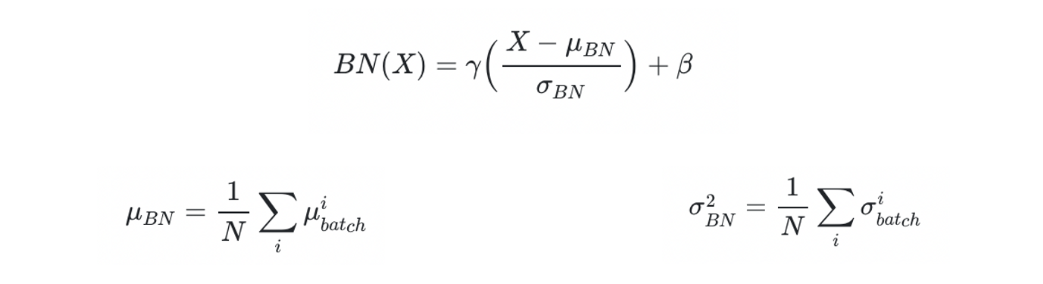
추론 과정의 batch normalization에 적용하는 평균과 분산은 고정값을 사용한다. 학습 단계에서처럼 데이터가 batch 단위로 들어오지 않기 때문에 학습 단계에서 저장된 batch 단위의 평균과 분산을 이용해 고정된 평균과 분산 값을 만들어 사용하는 것이다.
이 때 평균과 분산의 고정값은 학습 과정에서 이동 평균(moving average) 또는 지수 평균(exponential average)을 통하여 계산한 값이다. 이동 평균은 학습 시의 최근 N개의 데이터에 대한 평균과 분산값을 고정값으로 사용하고, 지수 평균은 전체 데이터에 대한 평균과 분산값을 고정값으로 사용한다. 또한, 이 때 사용되는 는 학습 과정에서 학습된 값이다.
이처럼 학습 과정과 추론 과정의 알고리즘이 다르므로, framework를 통해 구현할 때 옵션을 지정하여 평균과 분산값에 대해 moving average/variance를 사용하도록 설정해야 한다.
