그래프란?

정보를 정점과 간선으로 표현

1.Adjacency Matrix(인접 행렬)

int N = 6;
int[][] a = new int[N][N];

• N은 정점의 총수
• a[i][j] == 1 -> i와 j사이의 간선이 있다는 의미 (0의 없다는 의미)
• 간선에 방향이 없다면 i와j 사이에 간선이 있다는 의미임으로 a[i][j] == a[j][i]
• 간선에 방향이 있다면 a[i][j] == 1 or 0 이다.
• 간선에 3 가중치가 있다면 a[i][j] == 3이다.

2.Adjacency List(인접 리스트)

static final int N = 30; // 정점의 수 
ArrayList[] list = new ArrayList[N]; 
for (int i = 0; i < list.length; ++i) 
	list[i] = new ArrayList<Integer>(); 
    
a, b 사이 양방향 링크 추가
a, c 사이 양방향 링크 추가
list[a].add(b);
list[a].add(c);
list[c].add(a);
list[b].add(a);

N개의 링크드 리스트로 그래프를 표현한다.
N은 정점의 수이다.

3.Map으로 그래프 구현

가중치 없는 무향 그래프

public static Map<Character, String> createGraph1() {
		Map<Character, String> map = new HashMap<Character, String>();
		map.put('A', "BCD"); // A 정점에 인접한 정점 목록 등록
		map.put('B', "AC"); // B 정점에 인접한 정점 목록 등록
		map.put('C', "ABDE");
		map.put('D', "ACFG");
		map.put('E', "C");
		map.put('F', "DGH");
		map.put('G', "DFH");
		map.put('H', "FG");
		return map;
	}

가중치 없는 유향 그래프

public static Map<String, String[]> createGraph2() {
		Map<String, String[]> map = new HashMap<>();
		map.put("철수", new String[] { "영희", "동건", "준호", "승우" });
		map.put("영희", new String[] { "철수", "동건" });
		map.put("준호", new String[] { "철수", "승우" });
		map.put("승우", new String[] { "재상" });
		map.put("동건", new String[] { "영희", "재상" });
		map.put("재상", new String[] { "승우" });
		return map;
	}

가중치 있는 유향 그래프

class 인접정점 {
		public String 정점;
		public int 가중치;

		public 인접정점(String 정점, int 가중치) {
			this.정점 = 정점;
			this.가중치 = 가중치;
		}
	}
public static Map<String, 인접정점[]> createGraph3() {
		Map<String, 인접정점[]> map = new HashMap<>();
		map.put("철수", new 인접정점[] { new 인접정점("영희", 8), new 인접정점("동건", 7), new 인접정점("준호", 5), new 인접정점("승우", 6) });
		map.put("영희", new 인접정점[] { new 인접정점("철수", 9), new 인접정점("동건", 6) });
		map.put("준호", new 인접정점[] { new 인접정점("철수", 8), new 인접정점("승우", 5) });
		map.put("승우", new 인접정점[] { new 인접정점("재상", 1) });
		map.put("동건", new 인접정점[] { new 인접정점("영희", 9), new 인접정점("재상", 5) });
		map.put("재상", new 인접정점[] { new 인접정점("승우", 2) });
		return map;
	}
    

그래프 탐색 방법

너비우선탐색(BFS)과 깊이우선탐색(DFS)

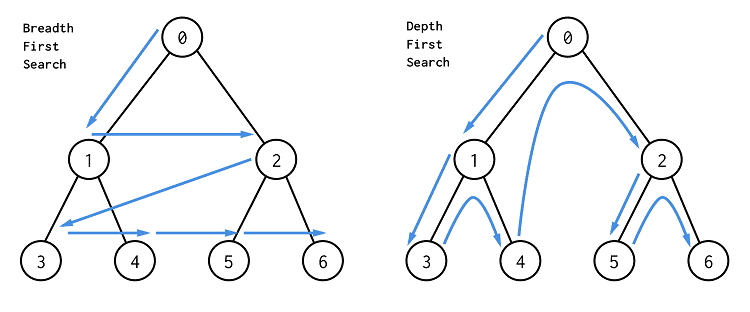
너비우선탐색(BFS)

시작점으로부터 시작해서
가까운 순서로 방문하는 것이다.

public static HashMap<Character, String> createGraph() {
		HashMap<Character, String> map = new HashMap<>();
		map.put('A', "BCD"); // A 정점에 인접한 정점 목록 등록
		map.put('B', "AC"); // B 정점에 인접한 정점 목록 등록
		map.put('C', "ABDE");
		map.put('D', "ACFG");
		map.put('E', "C");
		map.put('F', "DGH");
		map.put('G', "DFH");
		map.put('H', "FG");
		return map;
	}

public static void BFS(HashMap<Character, String> 그래프, char 시작정점) {
		HashSet<Character> 방문한정점 = new HashSet<>();
		Queue<Character> 다음에방문할정점목록 = new LinkedList<Character>();
		방문한정점.add(시작정점);
		다음에방문할정점목록.add(시작정점);
		while (다음에방문할정점목록.isEmpty() == false) {
			char 현재정점 = 다음에방문할정점목록.remove();
			System.out.printf("%c ", 현재정점);
			String 인접정점목록 = 그래프.get(현재정점);
			for (char 인접정점 : 인접정점목록.toCharArray())
				if (방문한정점.contains(인접정점) == false) {
					방문한정점.add(인접정점);
					다음에방문할정점목록.add(인접정점);
				}
		}
	}

public static void main(String[] args) {
		BFS(createGraph(), 'A');
	}

깊이우선탐색(DFS)

한쪽 경로로 갈수 있을 때까지 간 다음에
더 이상 못 가면 return 돌아오고
그 다음 경로를 시도하고 없다면 다시 return하는 방식이다.

public static HashMap<Character, String> createGraph() {
		HashMap<Character, String> map = new HashMap<>();
		map.put('A', "BCD"); // A 정점에 인접한 정점 목록 등록
		map.put('B', "AC"); // B 정점에 인접한 정점 목록 등록
		map.put('C', "ABDE");
		map.put('D', "ACFG");
		map.put('E', "C");
		map.put('F', "DGH");
		map.put('G', "DFH");
		map.put('H', "FG");
		return map;
	}

방법1) 재귀호출

static void DFS(HashMap<Character, String> 그래프, char 현재정점, HashSet<Character> 방문한정점) {
		방문한정점.add(현재정점);
		System.out.printf("%c ", 현재정점);
		String 인접정점목록 = 그래프.get(현재정점);
		for (char 인접정점 : 인접정점목록.toCharArray())
			if (방문한정점.contains(인접정점) == false)
				DFS(그래프, 인접정점, 방문한정점);
	}

실행결과 출력
A B C D F G H E

방법2) 반복문

public static void DFS(HashMap<Character, String> 그래프, char 시작정점) {
		HashSet<Character> 방문한정점 = new HashSet<>();
		Stack<Character> 다음에방문할정점목록 = new Stack<>();
		방문한정점.add(시작정점);
		다음에방문할정점목록.push(시작정점);
		while (다음에방문할정점목록.isEmpty() == false) {
			char 현재정점 = 다음에방문할정점목록.pop();
			System.out.printf("%c ", 현재정점);
			String 인접정점목록 = 그래프.get(현재정점);
			for (char 인접정점 : 인접정점목록.toCharArray())
				if (방문한정점.contains(인접정점) == false) {
					방문한정점.add(인접정점);
					다음에방문할정점목록.add(인접정점);
				}
		}
	}

실행결과 출력
A D G H F C E B

다음에 방문할 정점 목록을 Queue에 저장하면서 탐색하면 BFS 이고,
Stack에 저장하면서 탐색하면 DFS 이다.

실행결과가 다르지만 둘다 깊이 우선 탐색이 맞다.
출력 결과가 같을려면
인접한 노드 순서만 바꿔주면 된다.

public static HashMap<Character, String> createGraph() {
	HashMap<Character, String> map = new HashMap<>();
	map.put('A', "HFB"); // A 정점에 인접한 정점 목록 등록
	map.put('B', "FECA"); // B 정점에 인접한 정점 목록 등록
	map.put('C', "EDB");
	map.put('D', "EC");
	map.put('E', "DCB");
	map.put('F', "HGBA");
	map.put('G', "F");
	map.put('H', "FA");
	return map;
}