문제
가로 길이가 W cm, 세로 길이가 H cm인 직사각형 종이가 있다.
종이에는 왼쪽 위 꼭지점과 오른쪽 아래 꼭짓점을 연결하는 대각선이 그어져 있다
모든 격자칸은 1cm x 1cm 크기입니다.
대각선으로 직사각형을 자른다면 온전히 사용할수 있는 정사각형 개수를 구해라
가로의 길이 W와 세로의 길이 H가 주어질 때, 사용할 수 있는 정사각형의 개수를 구하는 solution 함수를 완성해 주세요.
제한사항
W, H : 1억 이하의 자연수
처음 문제보고는 멘붕이 였다.
알고리즘이란 불규칙해보이는 어떤것 안에서 패턴을 찾는거라고 생각하고
다른 분들꺼를 참고하고 또한 노가다로 패턴을 찾아보았다.
예를들어
W = 8
H = 12 인 직사각형이 있다면 그 안에는 96개의 정사각형이 있는데
대각선으로 자른다면 16개의 정사각형을 사용할수 없어 총 80개의 정사각형을 사용가능하다.
result = 80
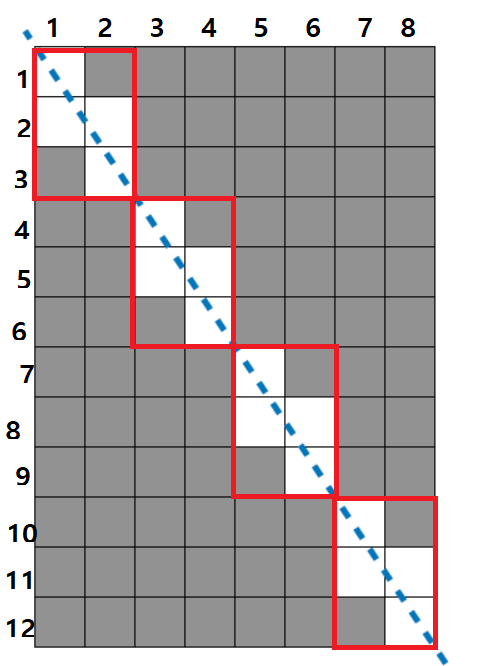
패턴을 찾아보자면 4번 같은 모양이 반복된다.
반복되는 패턴 직사각형의 꼭짓점 좌표를 구한다면
2/3
4/6
6/9
8/12
2, 4, 6, 8 은 2씩 증가하고
3, 6, 9, 12 는 3씩 증가한다.
각각 8은 2로 나누고 12는 3을 나눈다면 4라는 공통의 숫자가 나온다.
놀랍게도 4는 8과 12의 최대공약수이다.
최대공약수란..
8의 약수 : 1,2,4,8
12의 약수 : 1,2,3,4,6,12
공약수 : 1, 2, 4
최대공약수 : 4
그리고 패턴은 4번 반복되는데 최대공약수의 수와 같다.
이제는 저 패턴 직사각형안에서 버려야하는 정사각형을 어떻게 구할수 있을까?
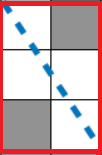
3*2에 버려야하는 정사각형은 4개이다.
규칙을 찾기위해서
예를 보자
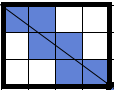
이것을 보자면
3*4에 버려야하는 정사각형은 6개이다.
3(N)+4(M)-1이다
규칙은 N+M-1이다
이제는 쉽다.
1. 두 변수(w,h)의 최대공약수를 찾는다.
2. 각각 두 변수를 최대공약수로 나눈다.
3. 하나의 패턴에 버려야할 정사각형의 수을 구한다.
4. 최대공약수와 버려야할 정사각형의 수을 곱한다.
5. w*h 값에다가 총 버려야할 정사각형의 수를 뺀다.
import java.math.BigInteger;
class Solution {
public long solution(long w, long h) {
long answer = 1;
long sum = w*h;
BigInteger b1 = BigInteger.valueOf(w);
BigInteger b2 = BigInteger.valueOf(h);
BigInteger gcd = b1.gcd(b2);
w=w/gcd.intValue();
h=h/gcd.intValue();
answer = sum-(w+h-1)*gcd.intValue();
return answer;
}주의! 에러가 난다면 w,h값이 크기 때문에 그런것이다. w,h를 long으로 타입를 바꾸자
