[딥러닝] 딥러닝 기초, 이진분류 XOR, 다중분류 MNIST, CNN, Scratch

Tensor Flow

머신러닝을 위한 오픈소스 플랫폼 - 딥러닝 프레임워크
구글이 개발, 코랩에는 기본으로 있음
Tensor : 벡터나 행렬
Graph : 텐서가 흐르는 경로 or 공간
Tensor Flow : 텐서가 그래프를 통해 흐른다
Keras는 텐서플로의 사용을 쉽게 해주기 위해 만들어짐

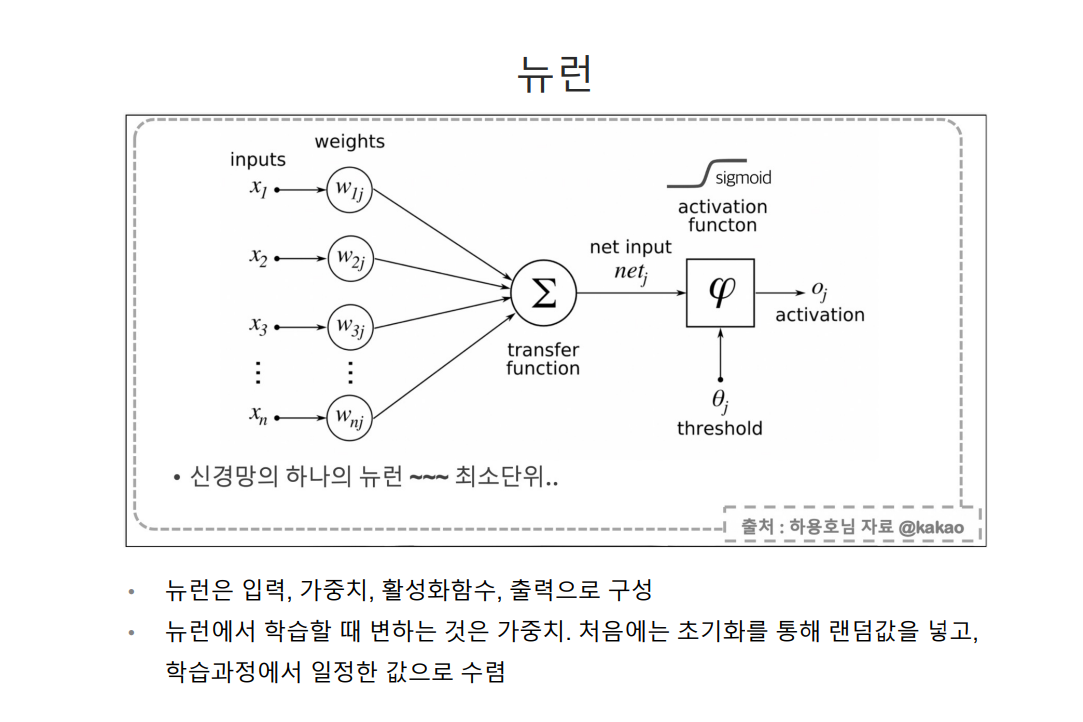
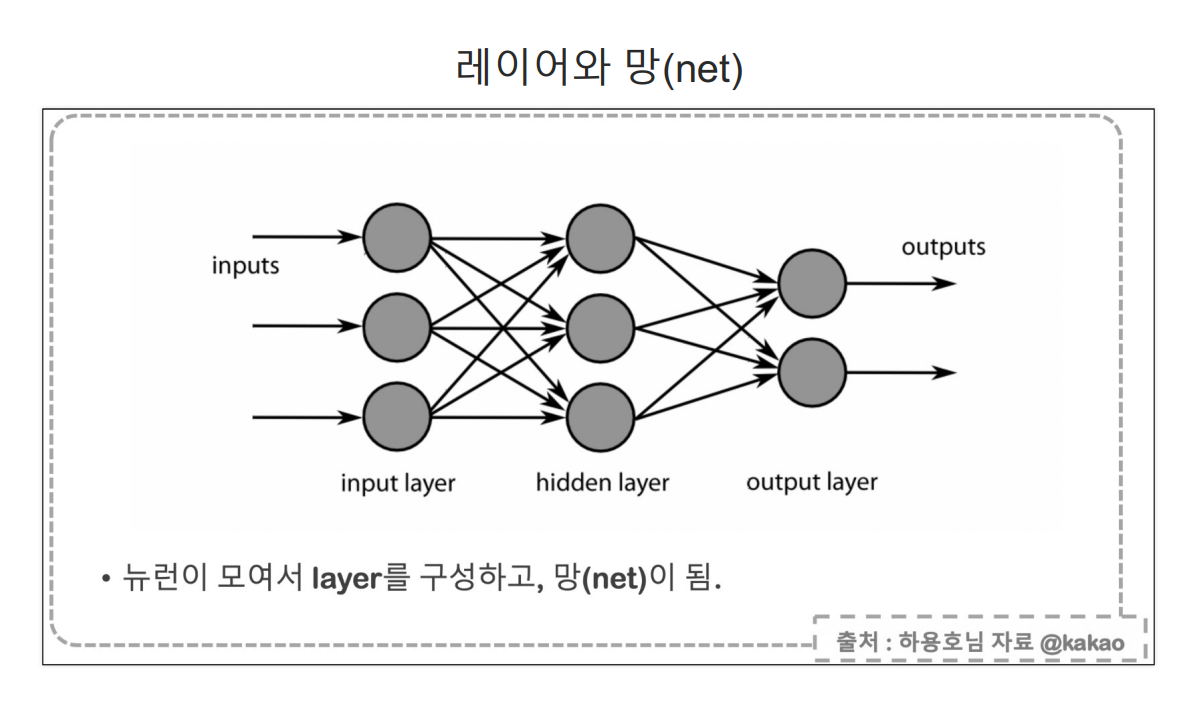
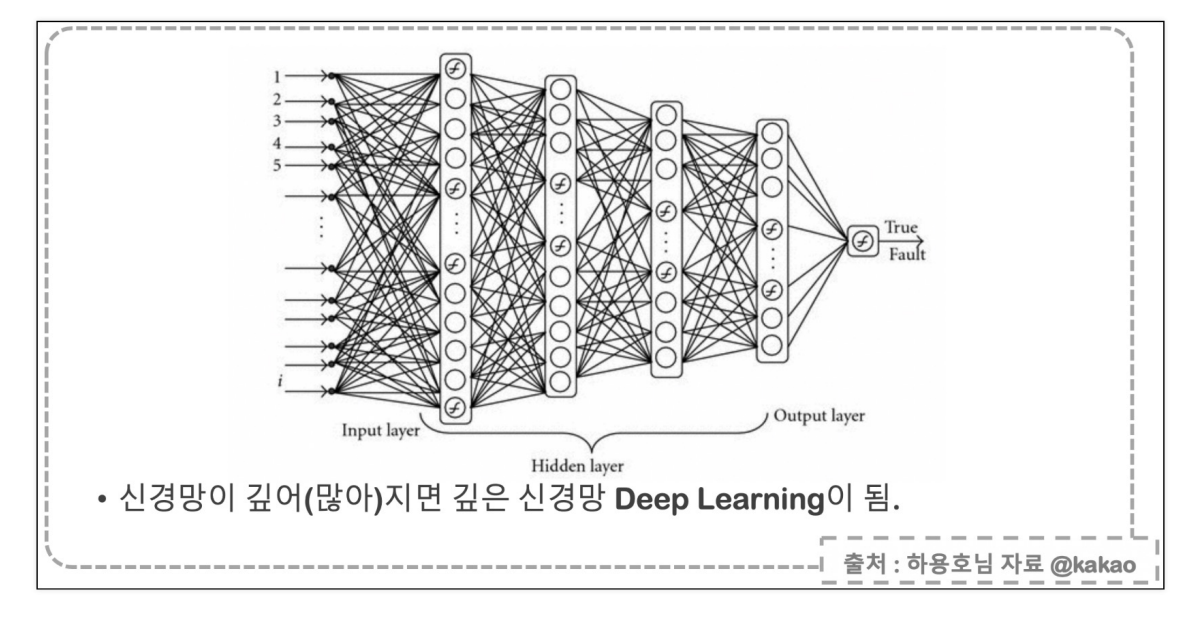
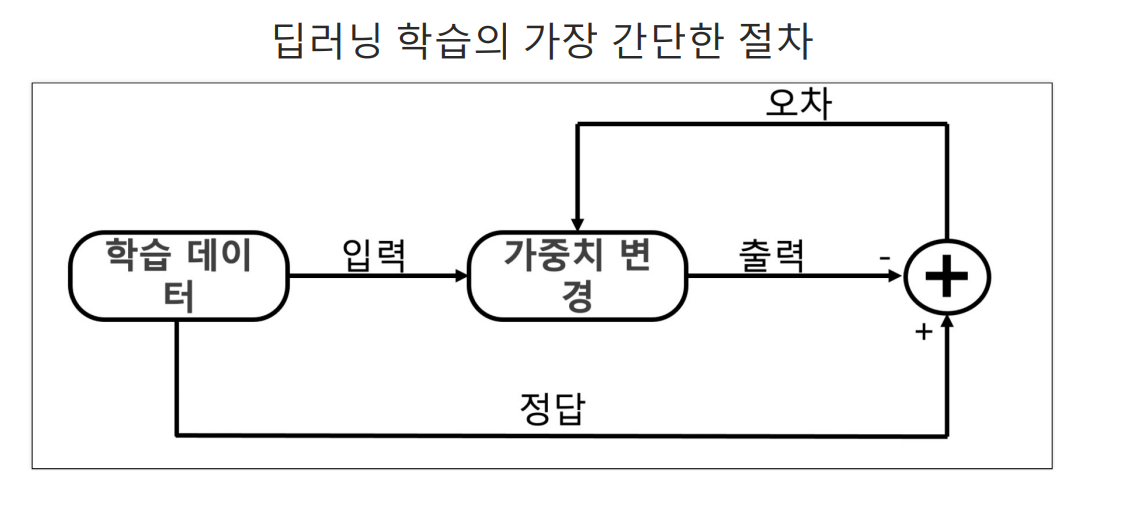
딥러닝이란?
어떤 모델을 선택할건지, 그 모델의 각 레이어들의 activation function은 뭘로 선택할지, 전체 레이어의 에러를 묘사하는 loss or cost function을 뭘로 잡을건지 / cost function을 최소화하는 그 길을 알려주는 최적화 방법을 뭘로 할건지, 학습을 몇번 돌릴지
이런 것들을 결정하는 절차를 거쳐가는 것

loss
loss(cost)함수는 정답까지 얼마나 멀리 있는지 측정하는 함수
mse:mean square error(오차 제곱의 평균)을 사용
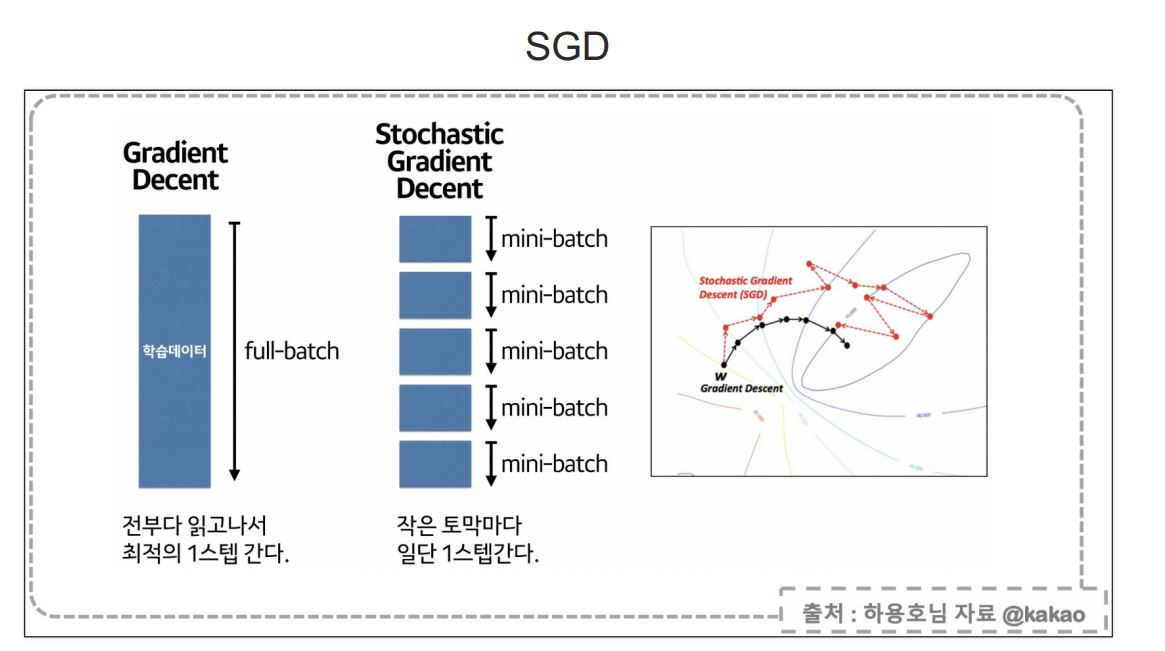
옵티마이저 선정(loss를 어떻게 줄일 것인지 결정하는 방법)

간단한 실습

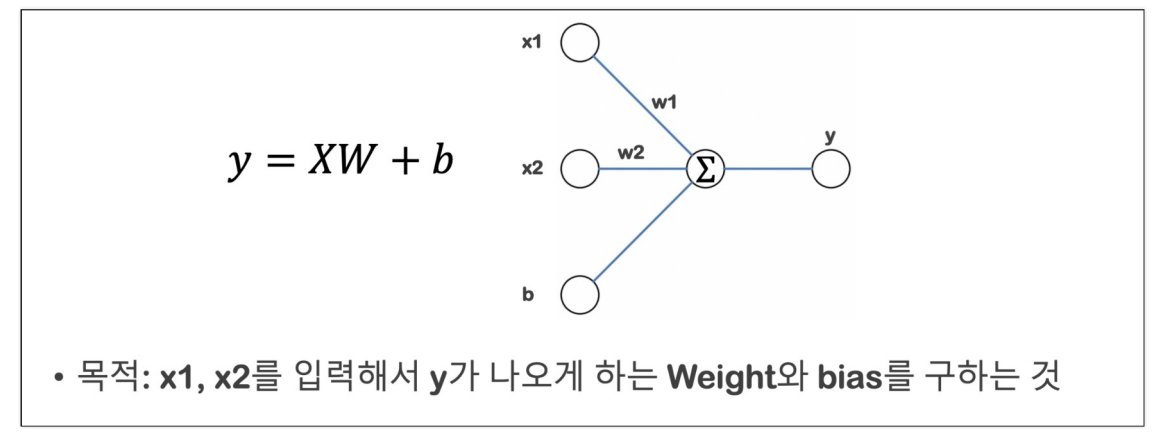
목표 : 나이와 몸무게를 알려주면 주어진 데이터 기준의 blood fat을 얻는 것 -> Linear Regression

blood fat을 추청하는 모델을 학습을 통해 얻는다.

• 모델 구성
• 모델의 loss function 선정
• loss 감소를 위한 optimizer 선정
• 학습
• predict

일단 데이터를 무작정 읽어보자

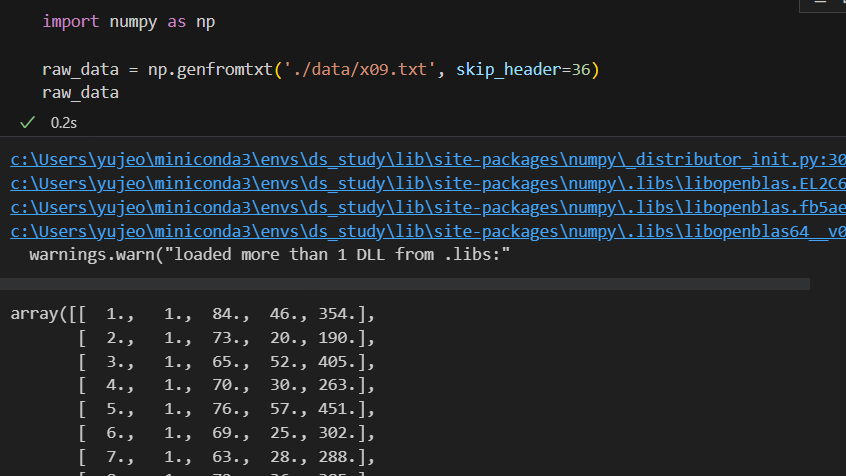
어떻게 생긴 데이터인지 확인

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt

xs = np.array(raw_data[:,2], dtype=np.float32)
ys = np.array(raw_data[:,3], dtype=np.float32)
zs = np.array(raw_data[:,4], dtype=np.float32)

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(xs,ys,zs)
ax.set_xlabel('Weight')
ax.set_ylabel('Age')
ax.set_zlabel('Blood fat')
ax.view_init(15,15)
plt.show()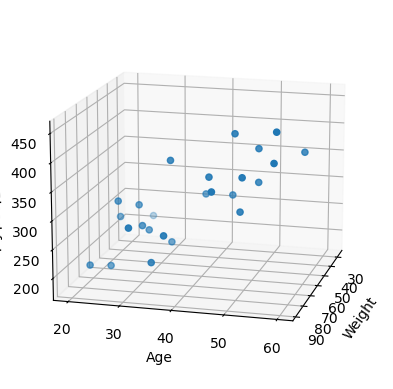

학습 대상 데이터를 추리고

x_data = np.array(raw_data[:,2:4], dtype=np.float32) #2,3번 컬럼이 feature data
y_data = np.array(raw_data[:,4], dtype=np.float32)

y_data = y_data.reshape((25,1))

원래 의도한 모델을 만들자

import tensorflow as tf

model = tf.keras.models.Sequential([
    tf.keras.layers.Dense(1, input_shape=(2,)) #1 : 출력이 하나, input_shape=(2, : 입력이 2개
])

model.compile(optimizer='rmsprop', loss='mse')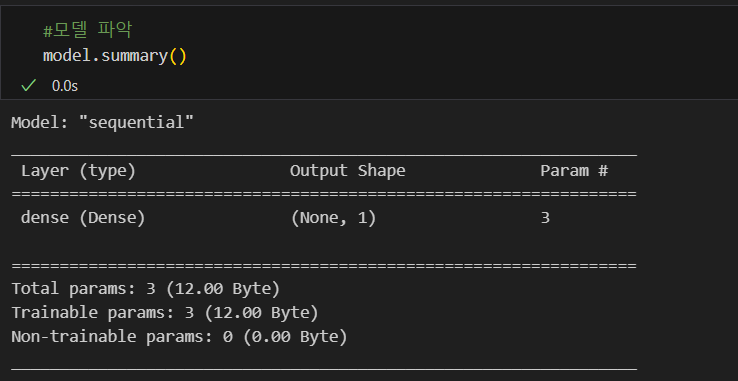

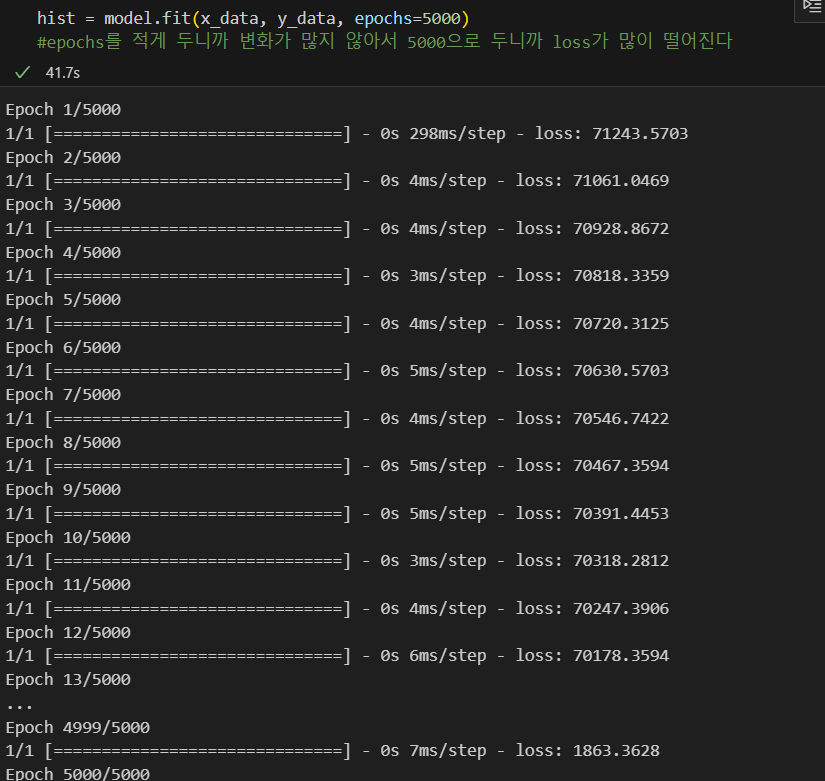
학습(fit)

확인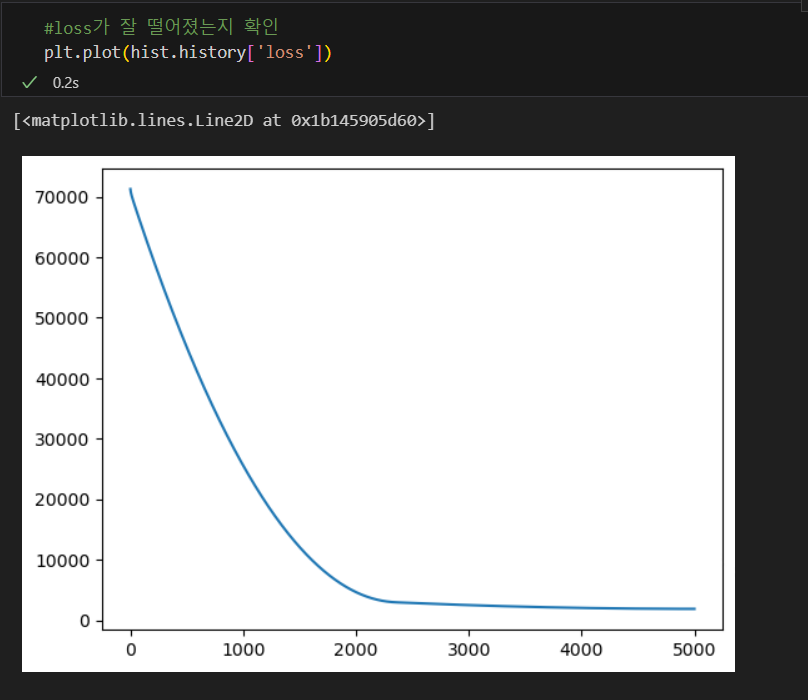
예측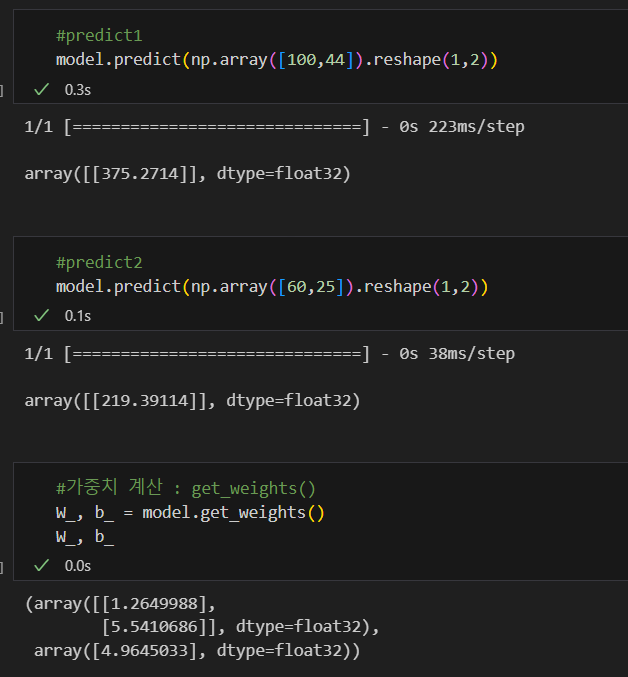

모델이 잘 만들어졌는지 확인하기 위해 데이터를 만들고, 그려보자

x = np.linspace(20,100,50).reshape(50,1)
y = np.linspace(10,70,50).reshape(50,1)

X = np.concatenate((x,y), axis=1)
Z = np.matmul(X,W_) + b_

fig = plt.figure(figsize=(12,12))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(xs, ys, zs)
ax.scatter(x,y,Z)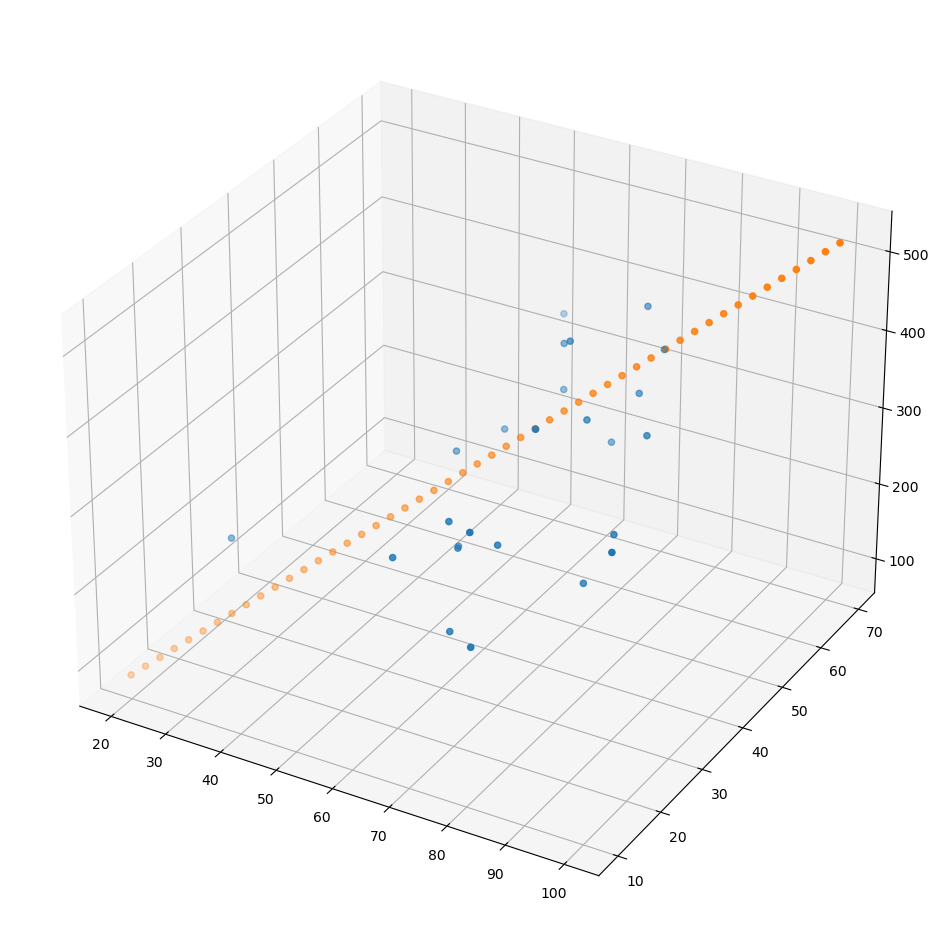

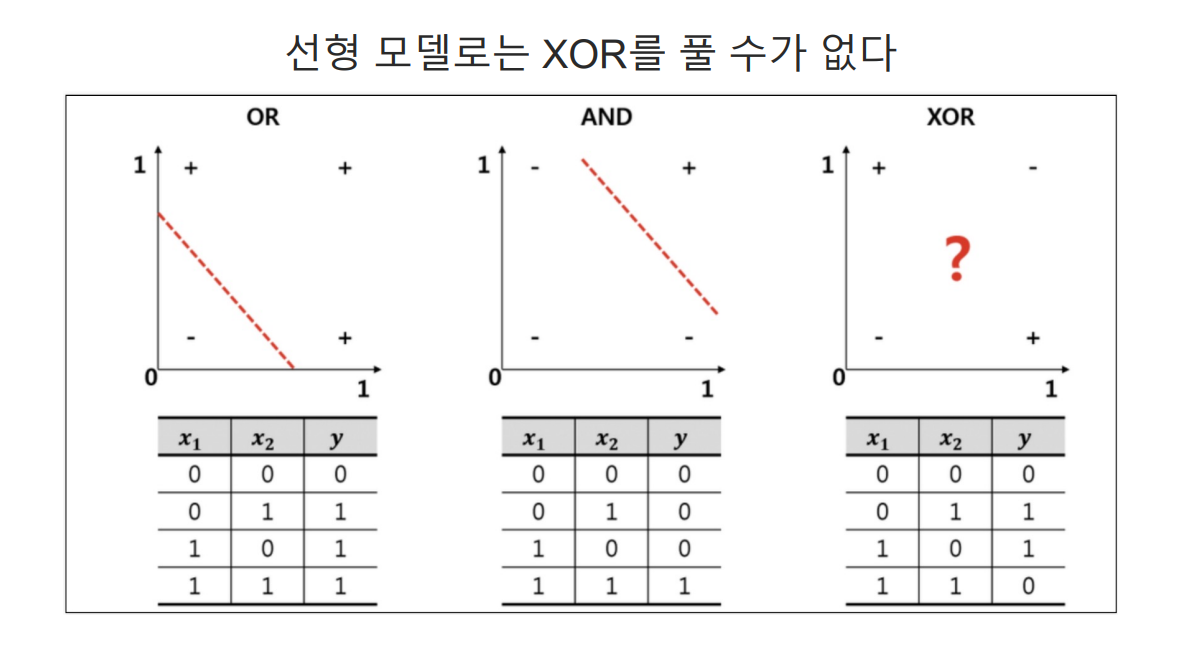
XOR

서로 다른 입력이 들어가면 출력이 1,
같은 입력이 들어가면 출력이 0으로 나온다

실습해보자

X = np.array([
    [0,0],
    [1,0],
    [0,1],
    [1,1]
])

y = np.array([[0], [1], [1], [0]])

model = tf.keras.Sequential([
    tf.keras.layers.Dense(2, activation='sigmoid', input_shape=(2,)),
    tf.keras.layers.Dense(1, activation='sigmoid')
])
# XOR 문제는 직선 하나로 해결할 수 없어서 직선 두 개를 사용
# 직선 두개를 합쳐서 또 선형이 되면 안되므로 비선형 함수 sigmoid를 통과시킨다

#model.compile
model.compile(optimizer=tf.keras.optimizers.SGD(lr=0.1), loss='mse')

모델을 그림으로 나타내면 아래와 같다

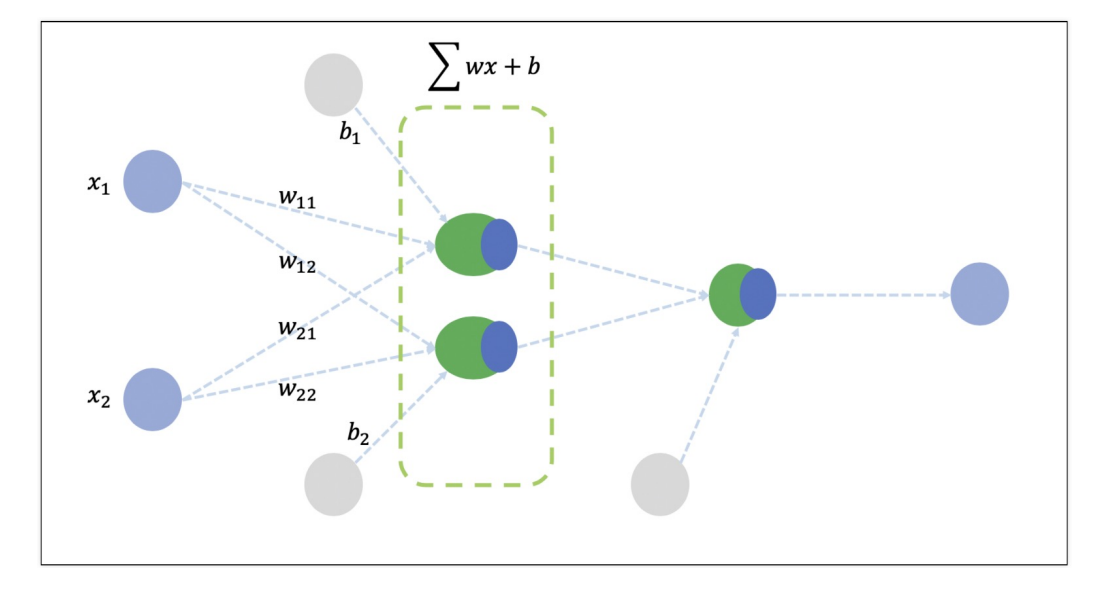
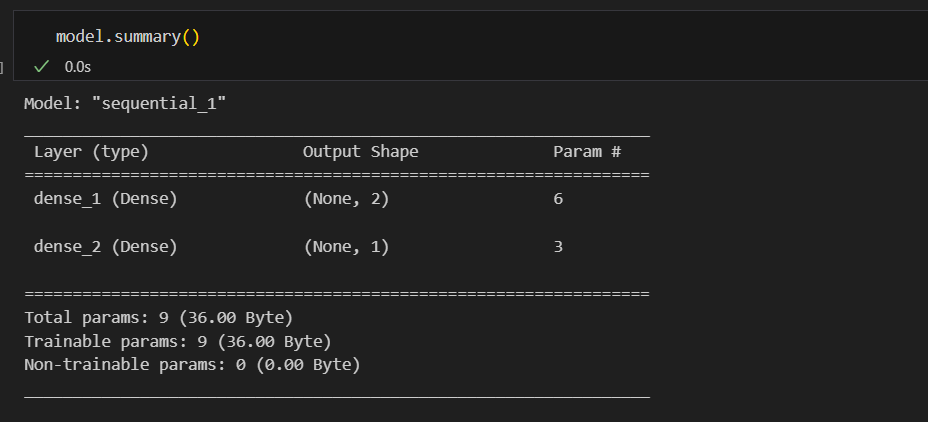
#학습
hist = model.fit(X, y, epochs=5000, batch_size=1) 
#epochs : 학습할 횟수
#batch_size 한번의 학습에 사용될 데이터의 수

학습 결과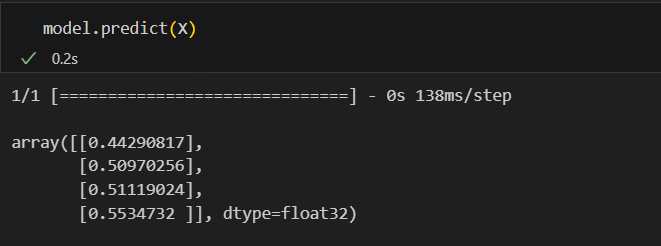
가중치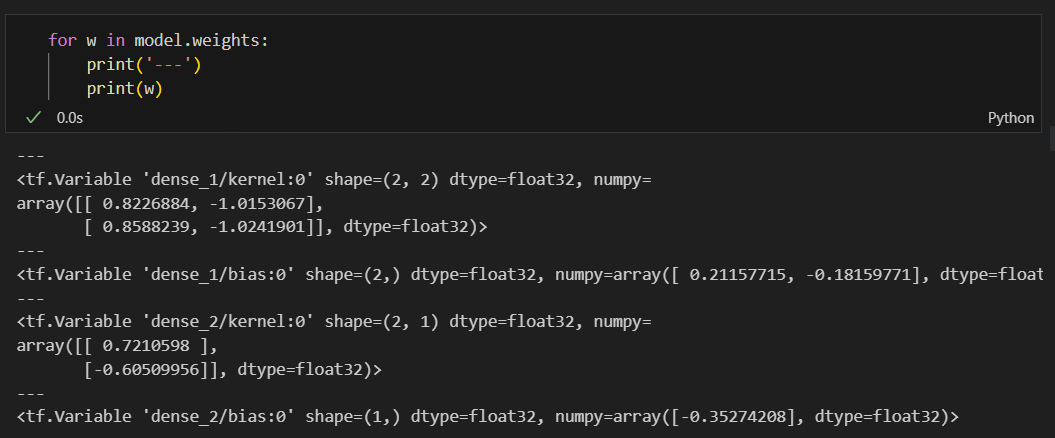

분류

iris 데이터

from sklearn.datasets import load_iris

iris = load_iris()

X = iris.data
y = iris.target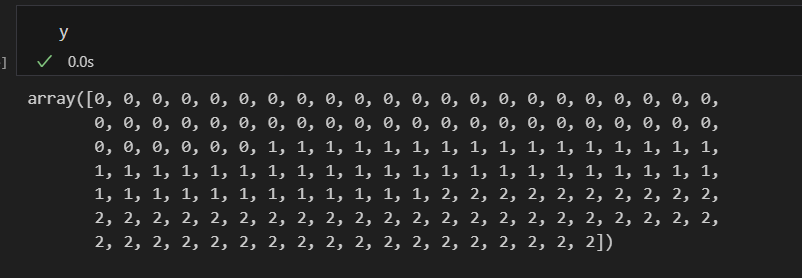

위와 같은 형태에서는
0이 답인데, 예측값이 0이라면 잘 맞춘것이지만
그런데 예측값이 1 이면 error는 1이고, 예측값이 2이면 error는 2라고 하는 것이 맞는 것인가?
이러한 문제를 해결하기 위해 one hot encoding 사용

sklearn의 one hot encoding

from sklearn.preprocessing import OneHotEncoder

enc = OneHotEncoder(sparse=False, handle_unknown='ignore')
enc.fit(y.reshape(len(y), 1))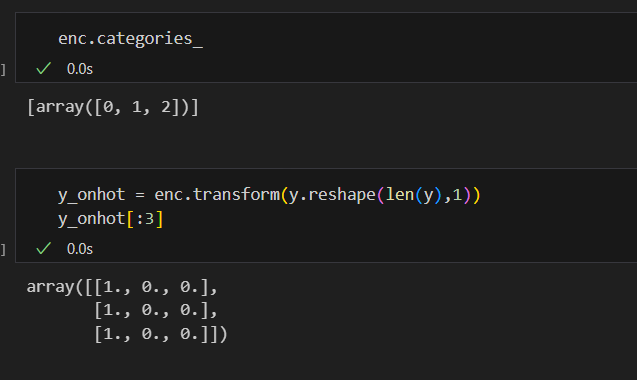

학습할 준비 완료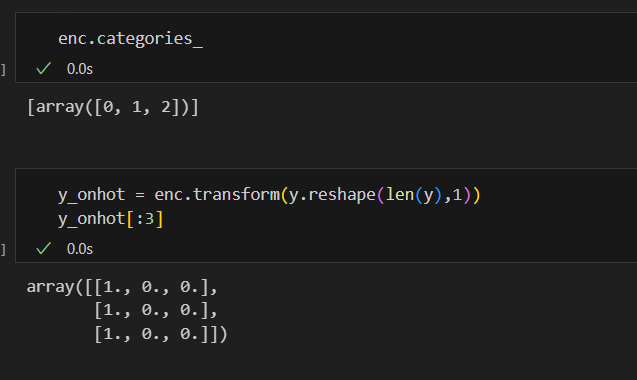

#데이터 나누기
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y_onhot, test_size=0.2, random_state=13)

#모델구성
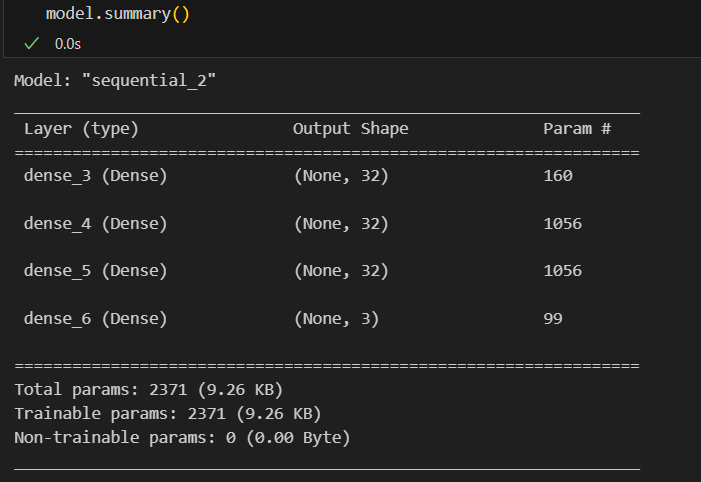
model = tf.keras.models.Sequential([
    tf.keras.layers.Dense(32, input_shape=(4,), activation='relu'),
    tf.keras.layers.Dense(32, activation='relu'),
    tf.keras.layers.Dense(32, activation='relu'),
    tf.keras.layers.Dense(3, activation='softmax')
])

#학습
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])

#fit
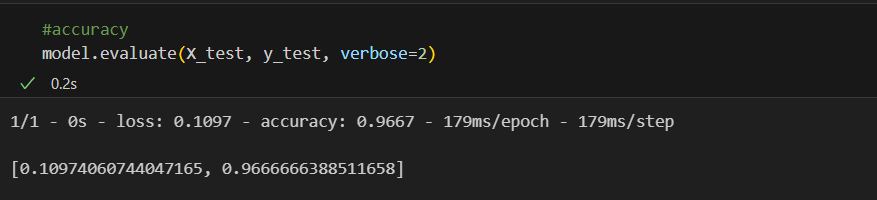
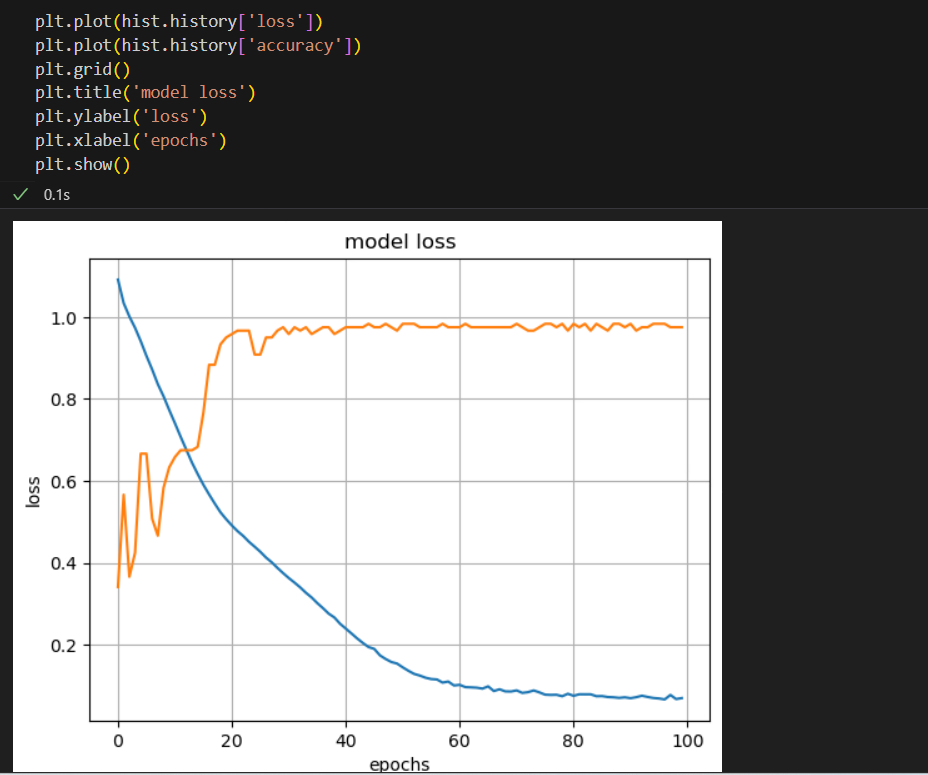
hist = model.fit(X_train, y_train, epochs=100)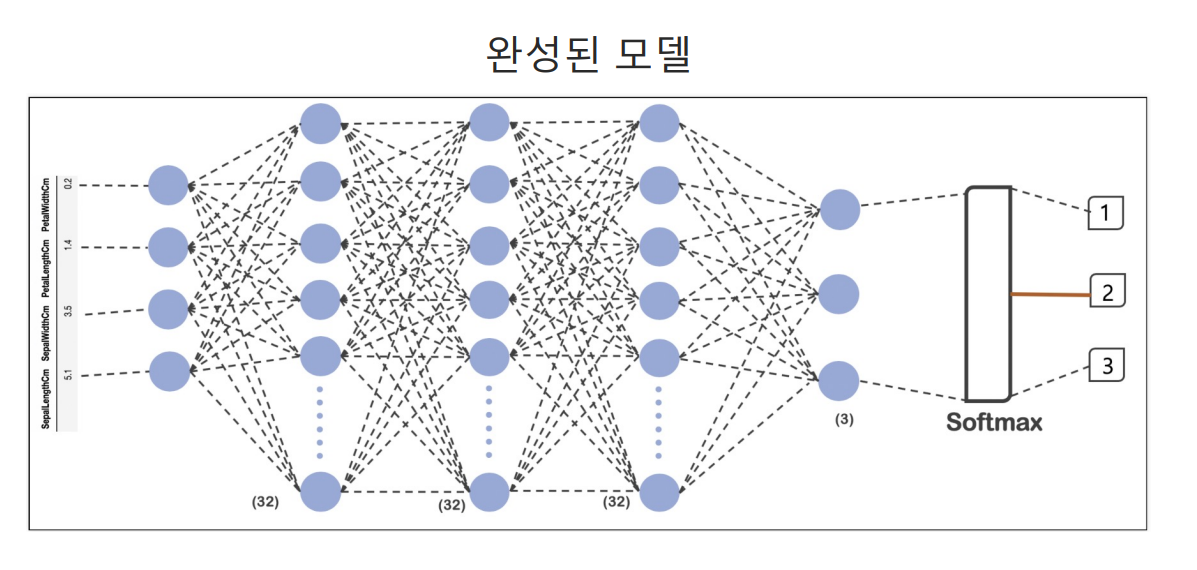

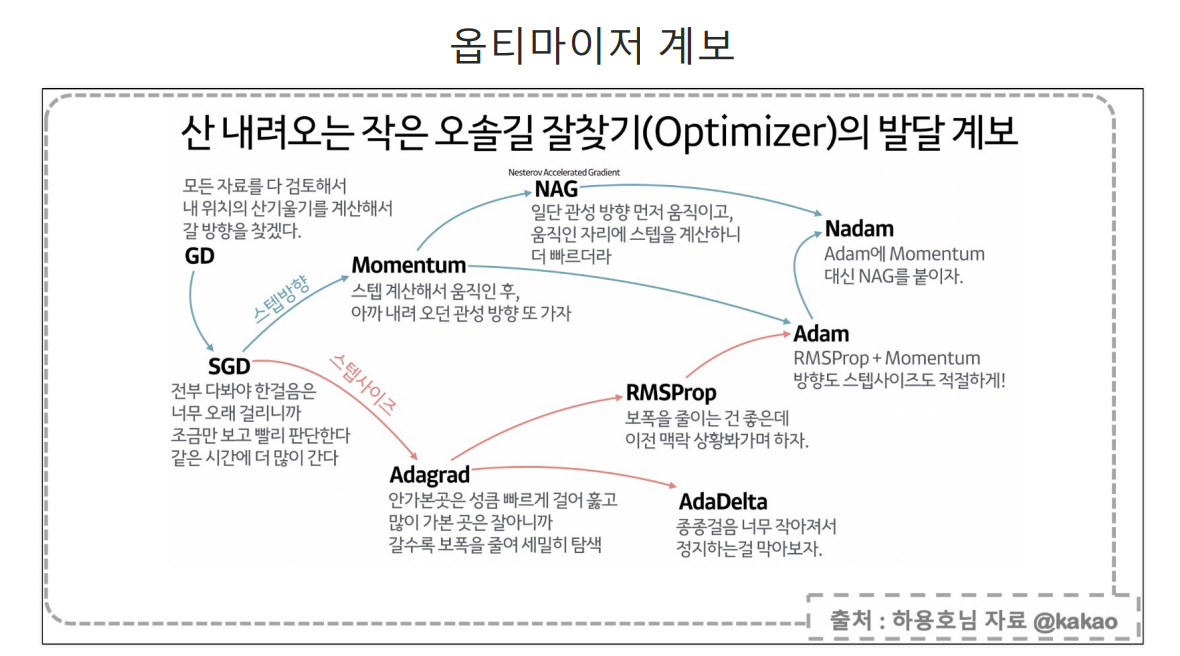
activation, SGD

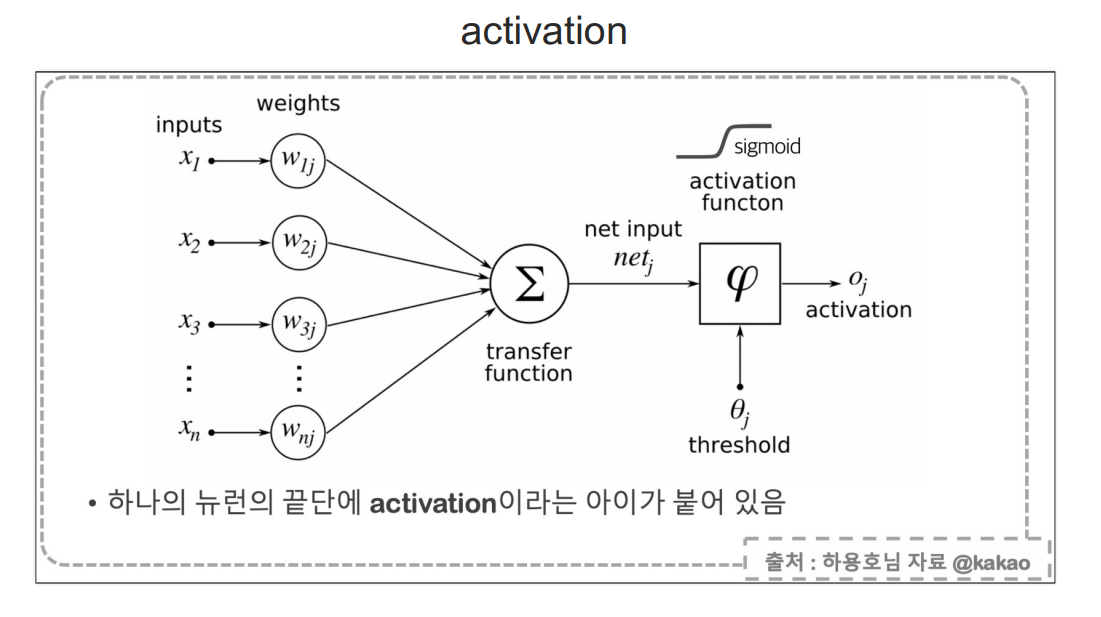
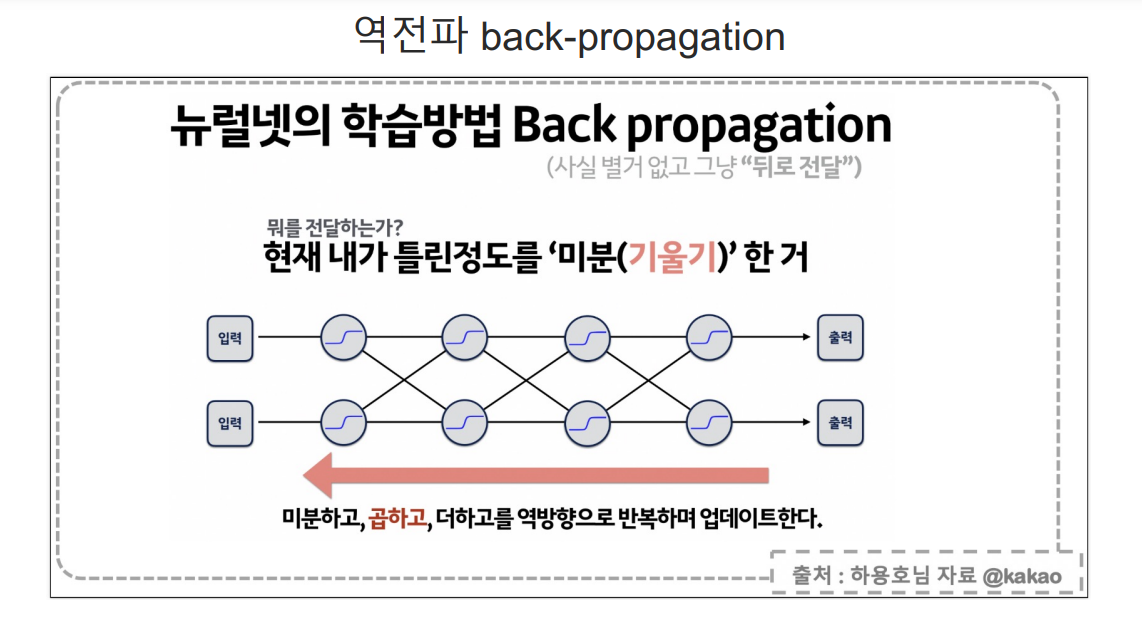
sigmoid는 layer가 깊을수록 역전파를 거치면 값이 매우매우 작아지는 문제가 있다.
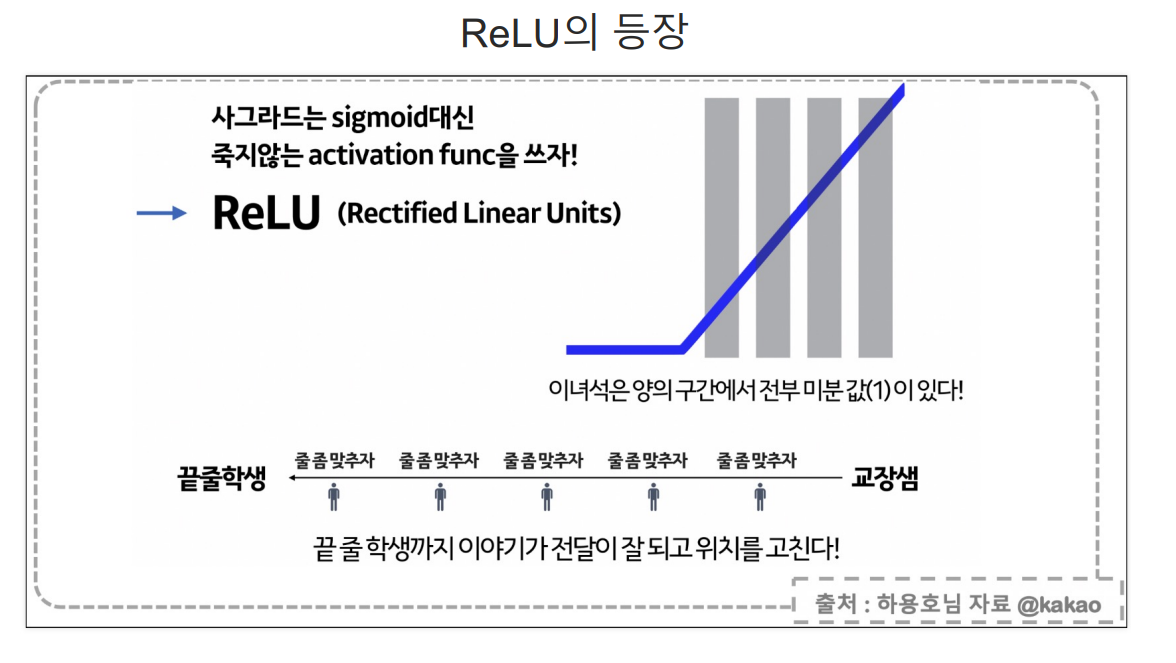
layer가 하나인 곳에서는 sigmoid는 문제가 없지만 layer가 많아지면 아래와 같은 문제가 발생한다.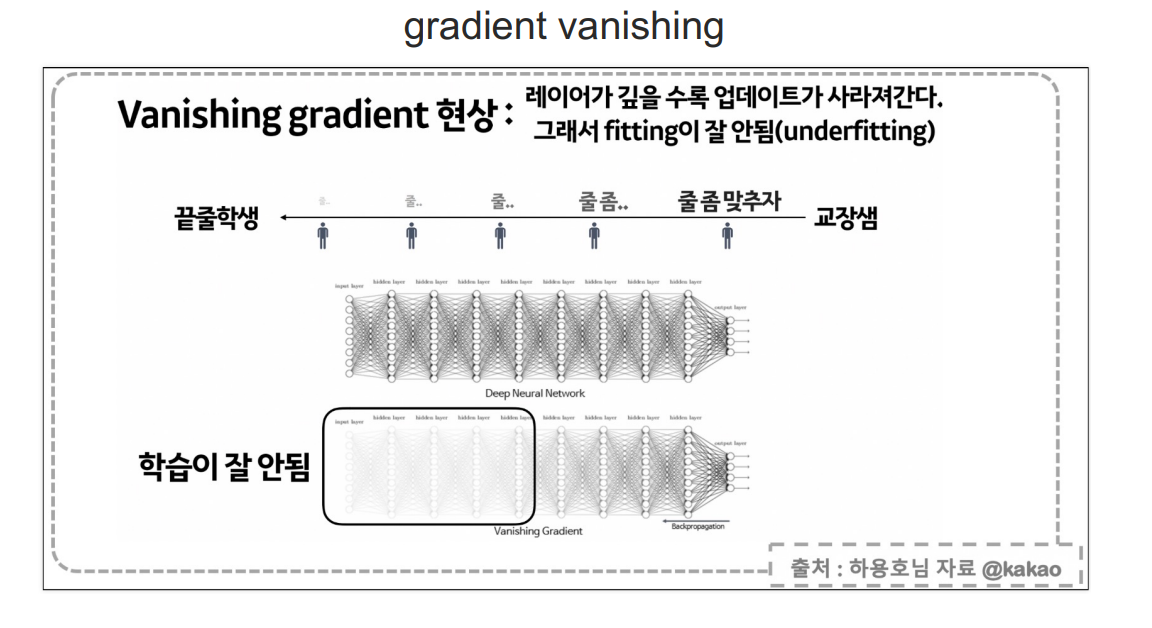sigmoid 대안으로 등장한 Relu

데이터가 복잡하거나 잘 모르겠으면 optimizer로 Adam을 써보자

딥러닝을 이용한 MNIST

데이터를 불러오자

import tensorflow as tf

mnist = tf.keras.datasets.mnist

(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train, x_test = X_train/255, X_test/255 #각 픽셀이 255값이 최댓값이어서 0~1사이의 값으로 조정 (일종의 min max scaler)

실습에 사용할 모델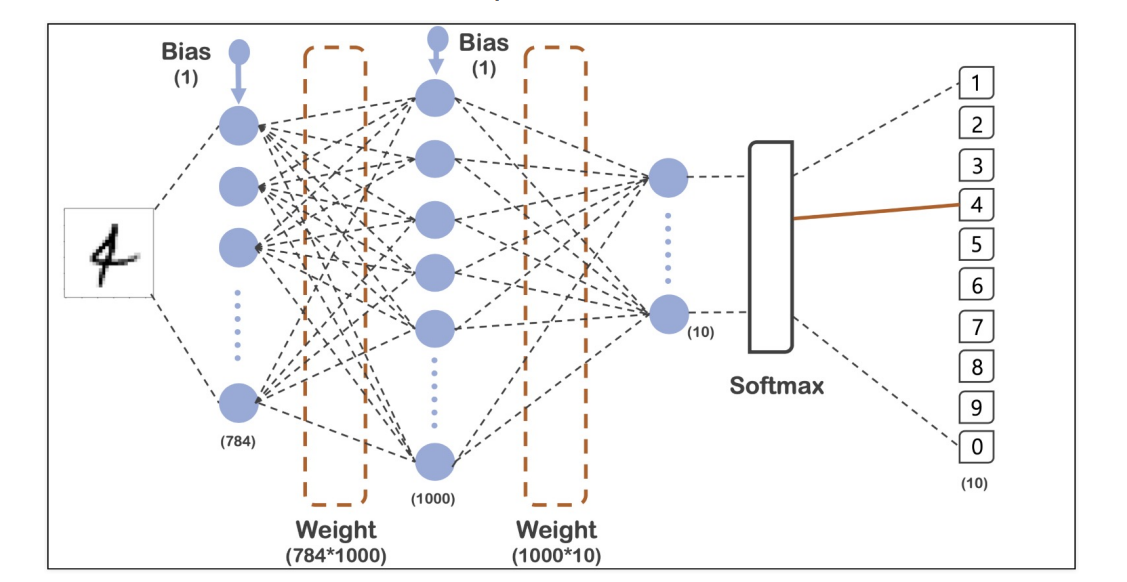

model = tf.keras.models.Sequential([
    tf.keras.layers.Flatten(input_shape=(28,28)), #Flatten : 일렬로 펼친다
    tf.keras.layers.Dense(1000, activation='relu'),
    tf.keras.layers.Dense(10, activation='softmax')
])

model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
#loss = 'sparse_categorical_crossentropy' : one-hot-encoding 효과
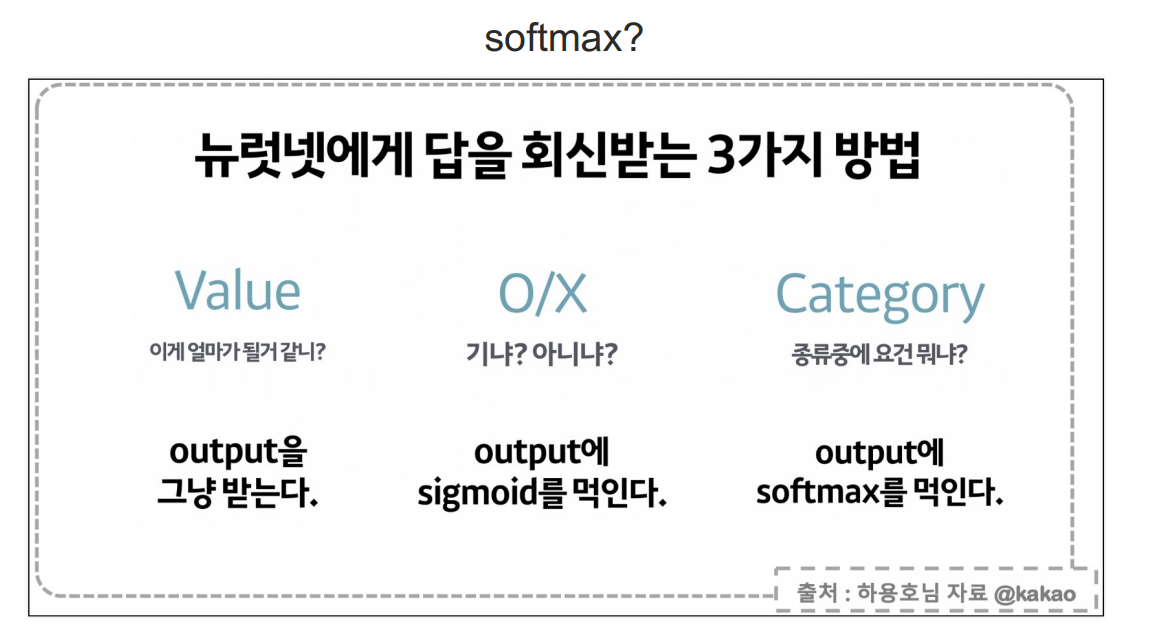
#softmax : 출력단이 여러개인 분류문제일때, 출력단의 합을 1로 만들어주고 제일 큰 값을
답이라고 하는 것

#fit
hist = model.fit(X_train, y_train, validation_data=(X_test, y_test), epochs=10, batch_size=100, verbose=1)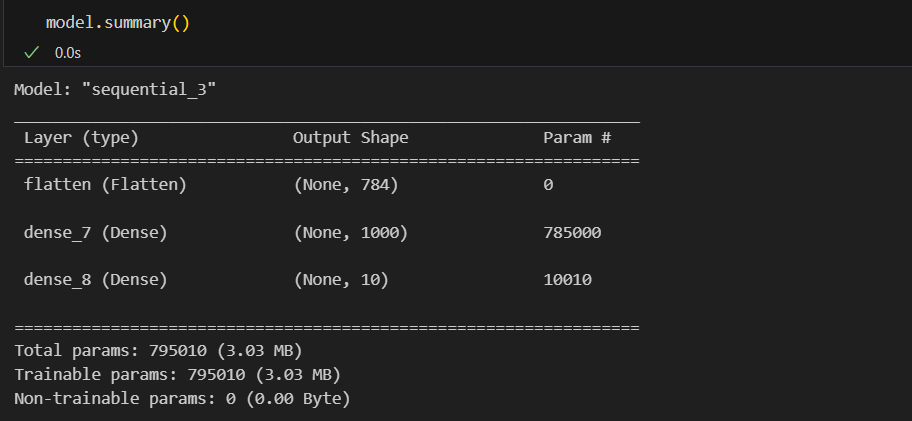

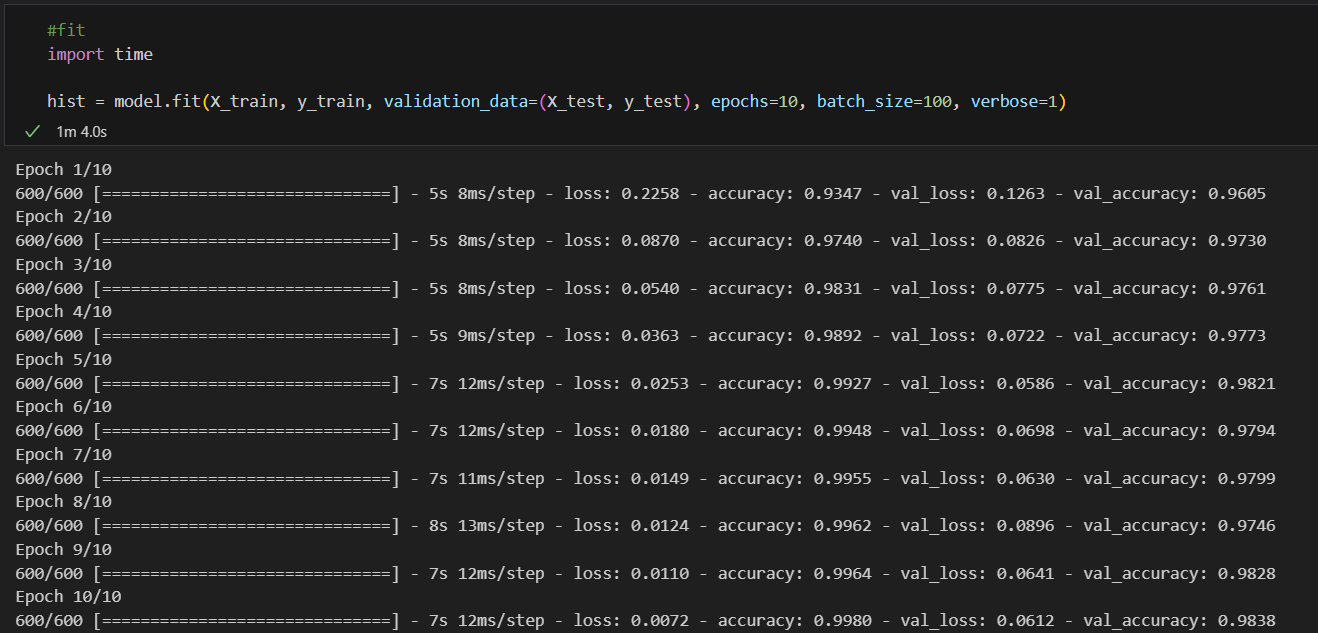
acc와 loss를 그려보자

import matplotlib.pyplot as plt

plot_target = ['loss', 'val_loss', 'accuracy', 'val_accuracy']
plt.figure(figsize=(12,8))

for each in plot_target:
    plt.plot(hist.history[each], label=each)

plt.legend()
plt.grid()
plt.show()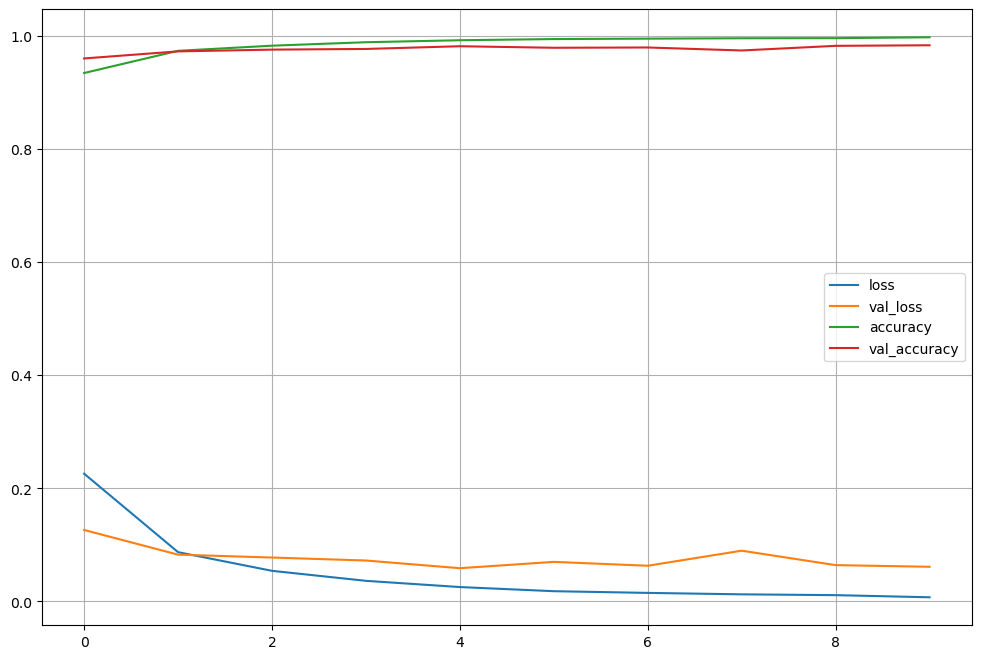

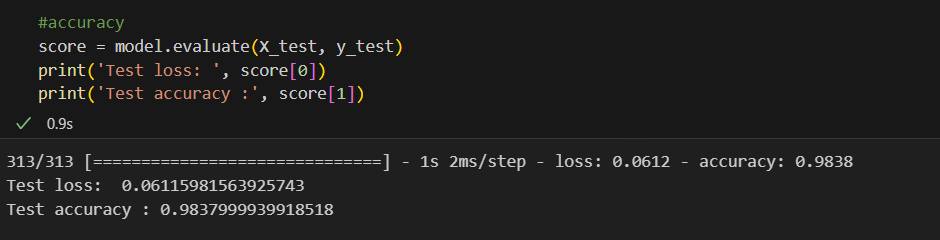머신러닝에서 93%쯤 나왔던 결과대비 5%쯤 향상되었다

뭐가 틀렸는지 확인해보자

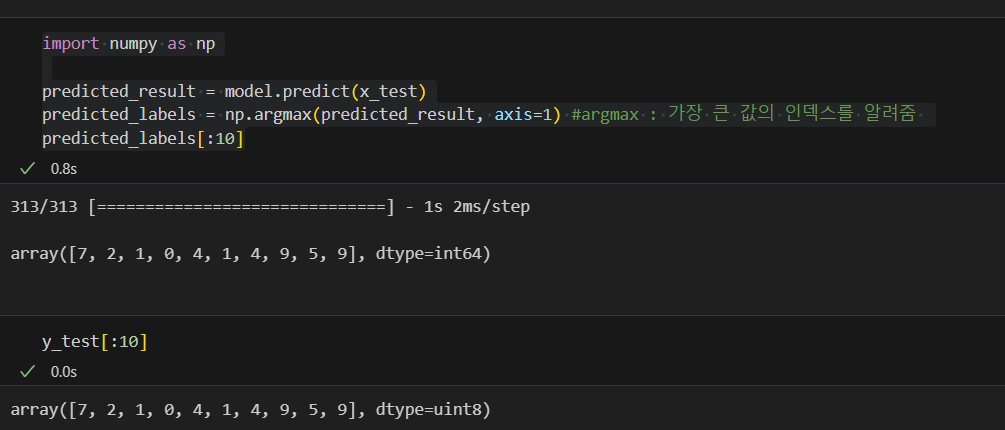
#틀린 데이터의 인덱스
wrong_result = []

for n in range(0, len(y_test)):
    if predicted_labels[n] != y_test[n]:
        wrong_result.append(n)

len(wrong_result)

#16개만
import random

samples = random.choices(population=wrong_result, k=16)

#확인
plt.figure(figsize=(14,12))

for idx, n in enumerate(samples):
    plt.subplot(4,4,idx+1)
    plt.imshow(x_test[n].reshape(28,28), cmap='Greys')
    plt.title('Label : ' + str(y_test[n]) + ' | predict : ' + str(predicted_labels[n]))
    plt.axis('off')

plt.show()

CNN

#데이터 받아오기
import tensorflow as tf

mnist = tf.keras.datasets.mnist

(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train, X_test = X_train/255, X_test/255

X_train = X_train.reshape((60000,28,28,1))
X_test = X_test.reshape((10000,28,28,1))

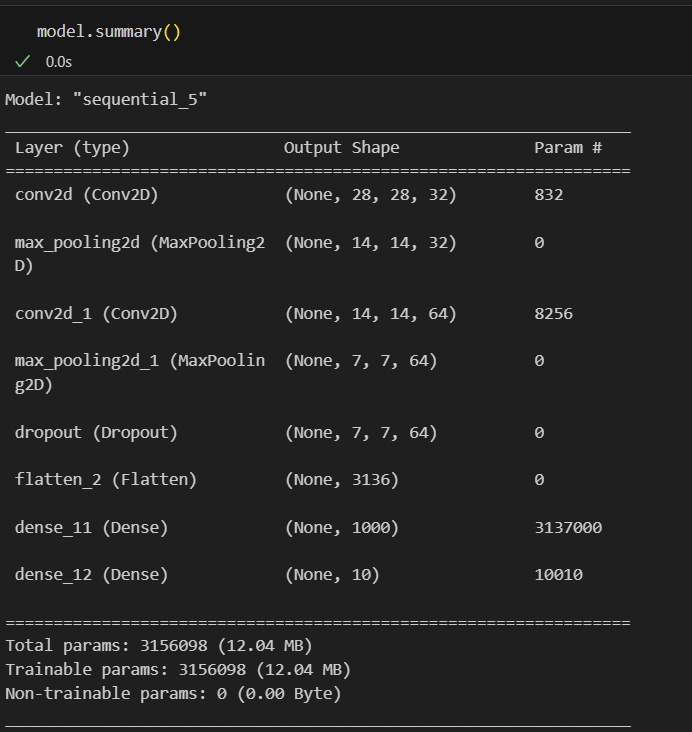
#모델 구성
from tensorflow.keras import layers, models

model = models.Sequential([
    layers.Conv2D(32, kernel_size=(5,5), strides=(1,1), padding='same', activation='relu', input_shape=(28,28,1)),
    layers.MaxPool2D(pool_size=(2,2), strides=(2,2)),
    layers.Conv2D(64, (2,2), activation='relu', padding='same'),
    layers.MaxPool2D(pool_size=(2,2), strides=(2,2)),
    layers.Dropout(0.25),
    layers.Flatten(),
    layers.Dense(1000, activation='relu'),
    layers.Dense(10, activation='softmax')
])

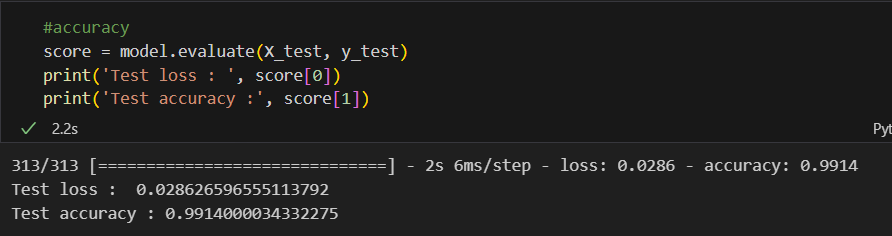
#학습
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])

hist = model.fit(X_train, y_train, epochs=5, verbose=1, validation_data= (X_test, y_test))

#학습 확인
import matplotlib.pyplot as plt
%matplotlib inline

plot_target = ['loss', 'val_loss', 'accuracy', 'val_accuracy']
plt.figure(figsize=(12,8))

for each in plot_target:
    plt.plot(hist.history[each], label=each)

plt.legend()
plt.grid()
plt.show()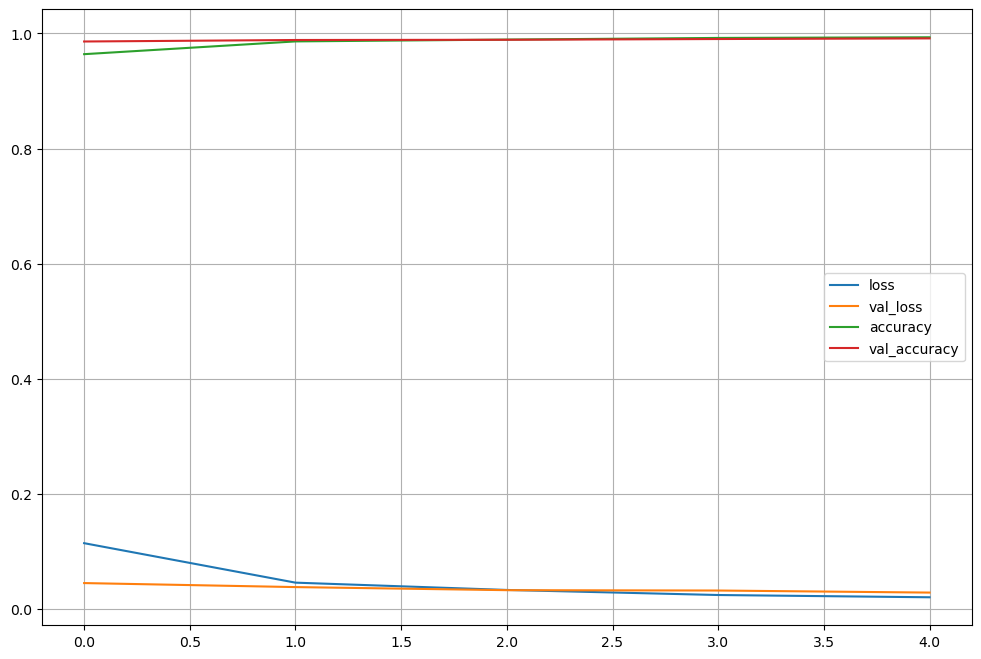

#모델 저장
model.save('MNIST_CNN_model.h5')

scratch

딥러닝을 numpy만으로 쌩으로 이해해보자

#데이터
import numpy as np

X = np.array([
    [0,0,1], #세번째에 있는 1은 b
    [0,1,1],
    [1,0,1],
    [1,1,1]
])

#시그모이드를 활성화 함수로
def sigmoid(x):
    return 1.0 / (1.0 + np.exp(-x))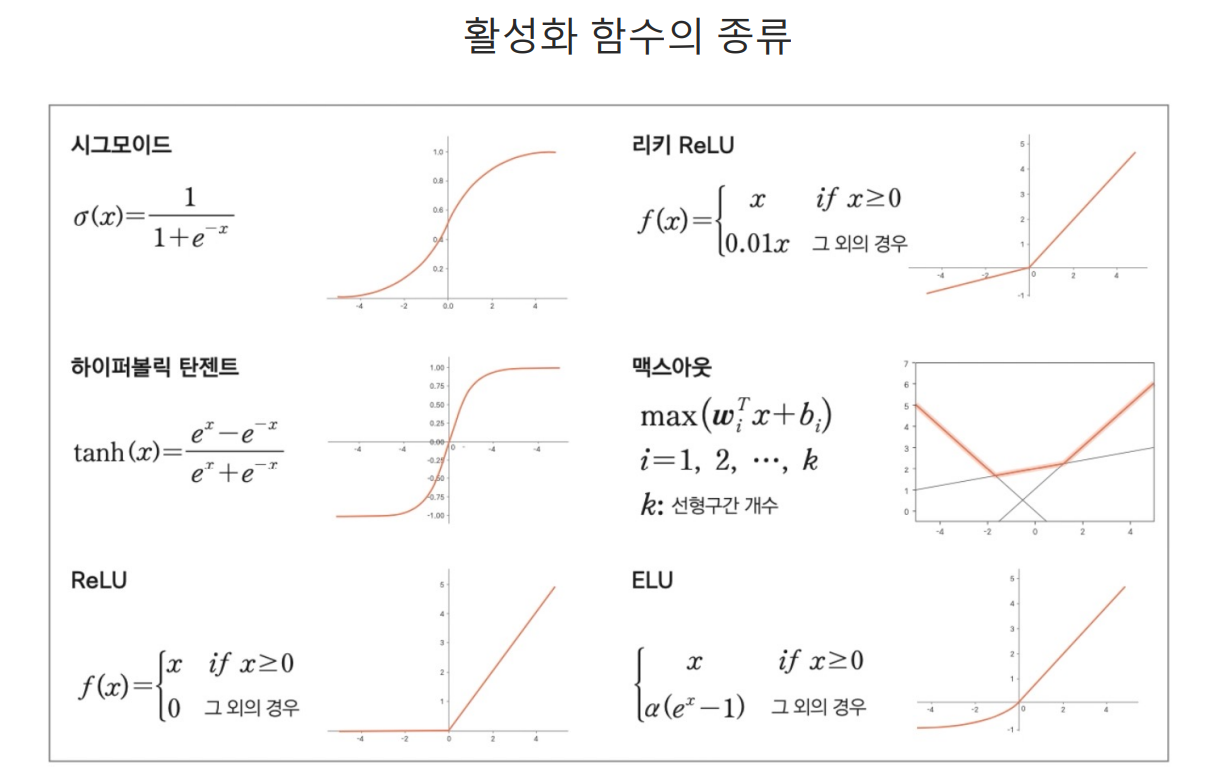

가중치를 랜덤하게 선택(원래는 학습이 완료된 가중치를 사용해야 한다)

#랜덤으로 가중치 선정
W = 2*np.random.random((1,3)) - 1 
#np.random.random((1,3))이 값은 항상 양수라서 음수도 나오도록 2를 곱하고 1을 빼줌

#추론결과
#순방향연산
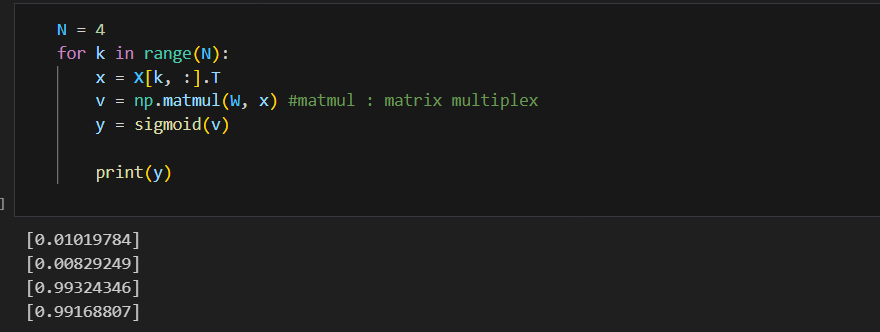
N = 4
for k in range(N):
    x = X[k, :].T
    v = np.matmul(W, x) #matmul : matrix multiplex
    y = sigmoid(v)

    print(v)

#np.matmul(W, X[0])
#np.matmul(W, X[1])
#np.matmul(W, X[2])
#np.matmul(W, X[3])

(결과)
[0.01019784]
[0.00829249]
[0.99324346]
[0.99168807]

가중치가 이제 정답을 맞추도록 학습을 시켜야 한다

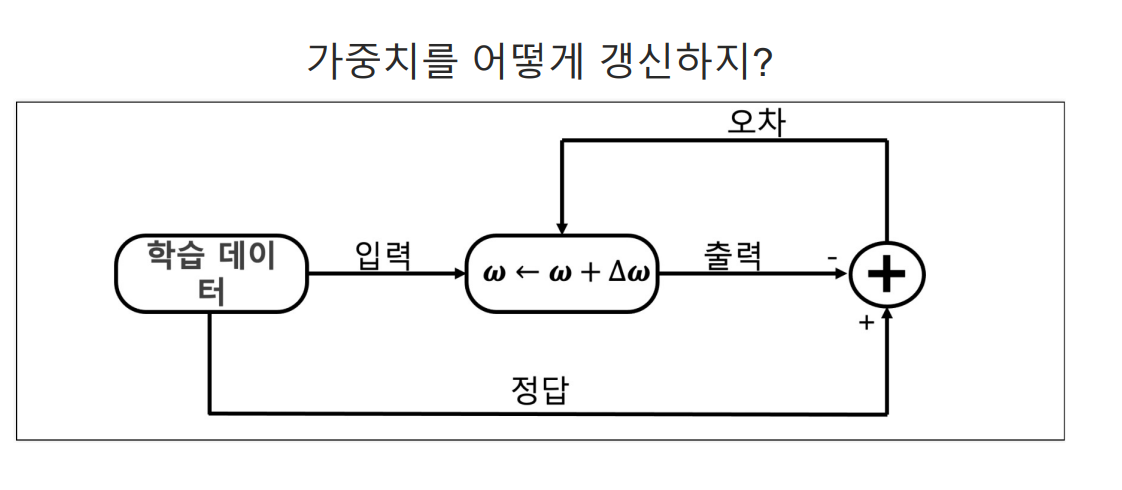
일단 정답을 주자 - AND

D = np.array([
    [0], [0], [1], [1]
])

#모델의 출력을 계산하는 함수(순방향 연산을 하는 추론과정)
def calc_output(W, x):
    v = np.matmul(W, x)
    y = sigmoid(v)

    return y
    
#오차 계산
def calc_error(d,y): #d:정답, y:추론값
    e = d - y #오차
    delta = y * (1-y) * e #y * (1-y) : 활성화 함수의 미분값

    return delta

시그모이드 함수 미분

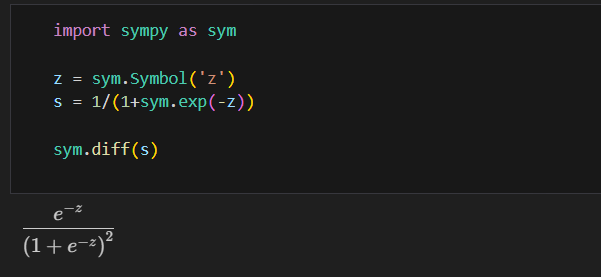
#한 epoch에 수행되는 W 계산
def delta_GD(W, X, D, alpha):
    for k in range(4):
        x = X[k, :].T
        d = D[k]

        y = calc_output(W,x)
        delta = calc_error(d, y)

        dW = alpha*delta*x
        W = W + dW
    
    return W

#가중치를 랜덤하게 초기화, 학습
W = 2*np.random.random((1,3)) - 1

alpha = 0.9
for epoch in range(10000):
    W = delta_GD(W, X, D, alpha)
    print(W)

<가중치가 변화가는 과정>

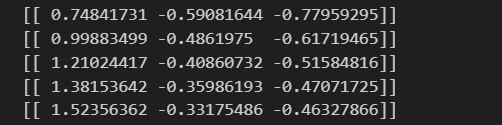
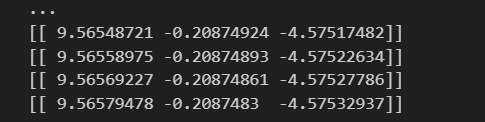
결과 확인

XOR

#XOR 데이터 다시 던져주고
X = np.array([
    [0,0,1], #세번째에 있는 1은 b
    [0,1,1],
    [1,0,1],
    [1,1,1]
])

D = np.array([[0], [1], [1], [0]])

W = 2*np.random.random((1,3)) - 1

#학습
alpha = 0.9
for epoch in range(10000):
    W = delta_GD(W, X, D, alpha)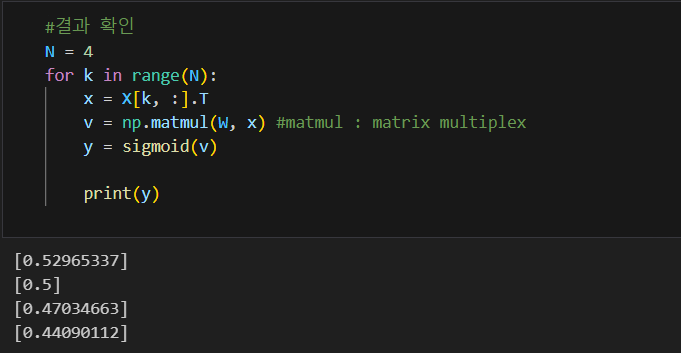

0 1 1 0이 답인데 1 1 0 0 정도로 나온 것.. 결과는 엉망인 셈

단층은 정답과 현재값의 오차를 계산하여 가중치를 갱신할 수 있지만,
다층의 경우 정답을 모르니까 1,2차 은닉층의 경우 오차를 계산할 수 없어서 가중치를 갱신할 수 없다.

따라서 역전파(Backpropagation)개념이 개발됨먼저 출력층의 오차 계산
출력층 가까이 있는 은닉층의 가중치와 델타 계산
다시 그 전 은닉층으로 계산

#output 계산 함수
def calc_output(W1, W2, x):
    v1 = np.matmul(W1, x)
    y1 = sigmoid(v1)
    v = np.matmul(W2, y1)
    y = sigmoid(v)

    return y, y14
    
#출력층의 델타 계산
def calc_delta(d,y): #d:정답, y:추론값
    e = d - y #오차
    delta = y * (1-y) * e #y * (1-y) : 활성화 함수의 미분값

    return delta
    
#은닉층의 델타 계산
def calc_delta1(W2, delta, y1):
    e1 = np.matmul(W2.T, delta)
    delta1 = y1*(1-y1)*e1

    return delta1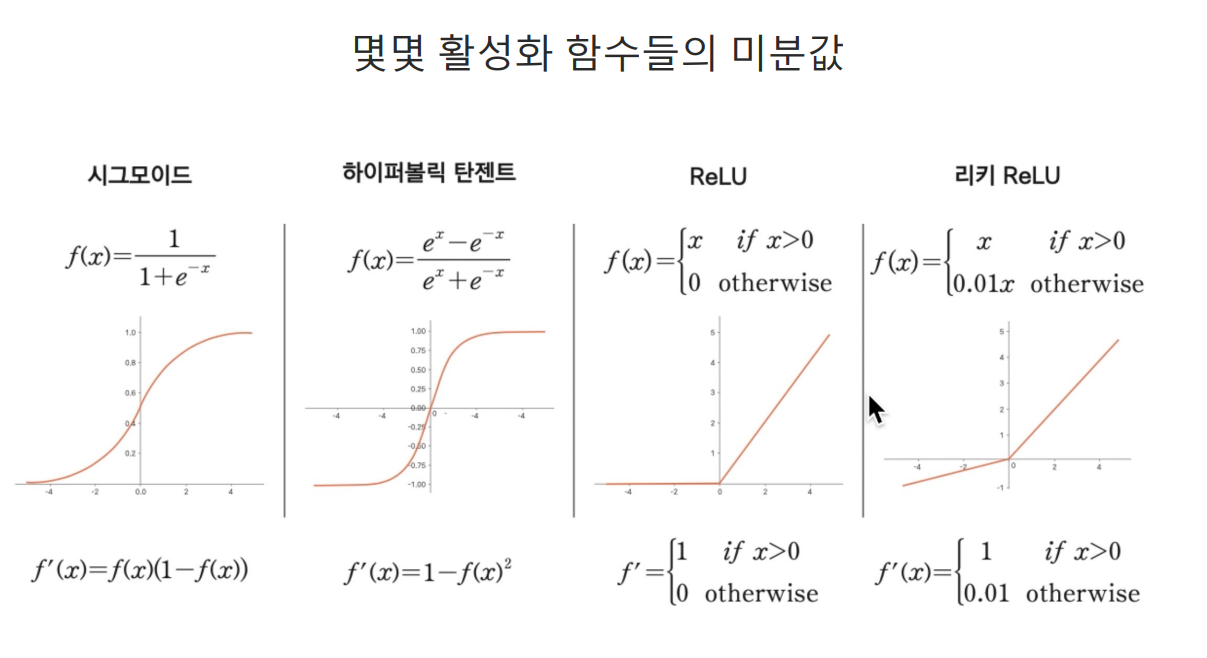    

#역전파
def backprop_XOR(W1, W2, X, D, alpha):
    for k in range(4):
        x = X[k, :].T
        d = D[k]

        y, y1 = calc_output(W1, W2, x)
        delta = calc_delta(d, y)
        delta1 = calc_delta1(W2, delta, y1)

        dW1 = (alpha*delta1).reshape(4,1)*x.reshape(1,3)
        W1 += dW1

        dW2 = alpha * delta * y1
        W2 += dW2 
    
    return W1, W2
    
#데이터를 준비하고 가중치를 랜덤하게 초기화
X = np.array([
    [0,0,1], #세번째에 있는 1은 b
    [0,1,1],
    [1,0,1],
    [1,1,1]
])

D = np.array([[0], [1], [1], [0]])

W1 = 2*np.random.random((4,3)) - 1
W2 = 2*np.random.random((1,4)) - 1

#학습
alpha = 0.9
for epoch in range(10000):
    W1, W2 = backprop_XOR(W1, W2, X, D, alpha)
    
#결과
N = 4
for k in range(N):
    x = X[k, :].T
    v1 = np.matmul(W1, x) #matmul : matrix multiplex
    y1 = sigmoid(v1)
    v = np.matmul(W2, y1) #matmul : matrix multiplex
    y = sigmoid(v)

    print(y)
    
[0.00678143]
[0.98975111]
[0.98662317]
[0.0166425]

loss 함수를 교체해보자

#cross_entropy의 델타
def calcDelta_ce(d,y):
    e = d- y
    delta = e

    return e
#cross entropy함수를 사용하면 델타는 오차와 같다

#은닉층에서
def calcDelta1_ce(W2, delta, y1):
    e1 = np.matmul(W2.T, delta)
    delta1 = y1*(1-y1)*e1

    return delta1

#역전파
def BackpropCE(W1, W2, X, D, alpha):
    for k in range(4):
        x = X[k, :].T
        d = D[k]

        y, y1 = calc_output(W1, W2, x)
        delta = calcDelta_ce(d,y)
        delta1 = calcDelta1_ce(W2, delta, y1)

        dW1 = (alpha*delta1).reshape(4,1) * x.reshape(1,3)
        W1 += dW1

        dW2 = alpha * delta * y1
        W2 += dW2

    return W1, W2
    
#학습
W1 = 2*np.random.random((4,3)) - 1
W2 = 2*np.random.random((1,4)) - 1

alpha = 0.9
for epoch in range(10000):
    W1, W2 = BackpropCE(W1, W2, X, D, alpha)
    
#결과
N = 4
for k in range(N):
    x = X[k, :].T
    v1 = np.matmul(W1, x) #matmul : matrix multiplex
    y1 = sigmoid(v1)
    v = np.matmul(W2, y1) #matmul : matrix multiplex
    y = sigmoid(v)

    print(y)
    
[3.52545677e-05]
[0.9998873]
[0.99976132]
[0.00035861]