사용 목적
▶ 최솟값이나 최댓값을 빠르게 찾아내기 위해서 ( 완전 이진 트리를 기반)
최대힙 : 부모노드 값 > 자식 노드
최소힙 : 부모노드 값 < 자식노드
시간 복잡도
▶ O(N * log N)
: 한 번 자식 노드로 내려갈 때마다 노드의 갯수가 2배씩 증가한다는 점 (ex 데이터의 갯수가 1024개라면 대략 10번만 내려가도 됨)
메모리 측면
▶ 효율적
: 별도로 추가적인 배열이 필요하지 않다는 점에서 몹수 효율적. 힙 정렬이 우위긴 하지만 단순히 속도면에서는 퀵정렬이 빠르기에 힙정렬이 많이 사용되지는 않음.
자료구조 Heap 이란?
- 완전 이진 트리의 일종으로 우선순위 큐( 가장 우선순위가 높은 데이터 삭제) 를 위하여 만들어진 자료구조.
- 힙은 일종의 반정렬 상태(느슨한 정렬 상태) 를 유지한다.
- 큰 값이 상위 레벨에 있고 작은 값이 하위 레벨에 있다 = 최대힙 구조
출처 : https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html
힙정렬을 공부하기전 이진트리란?
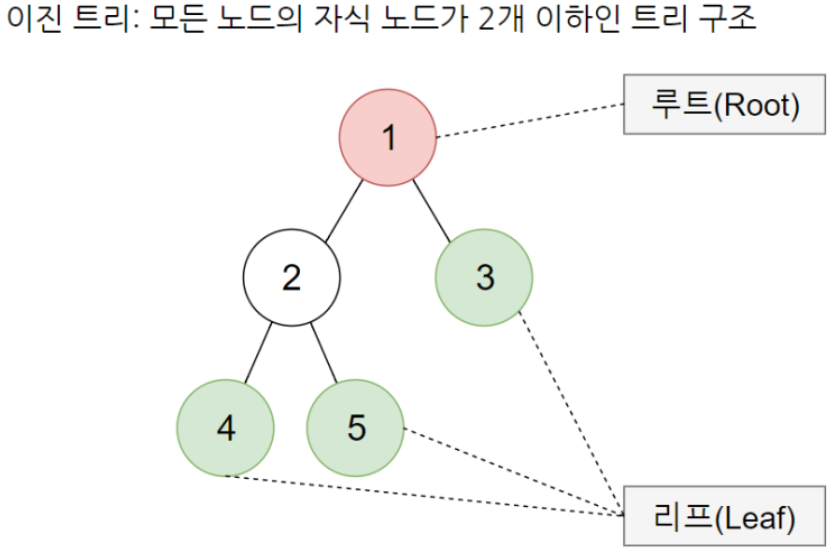
- 이진트리란 컴퓨터 안에서 각 노드에 담은 데이터(부모노드) 뒤에 노드를 두 개씩 이어붙이는(자식 노드) 구조다
- 모든 노드의 자식노드가 2개 이하인 노드.
- 나무의 형태처럼 가지를 뻗어나가는 것 같이 데이터가 서로 연결돼있음.
완전 이진 트리란?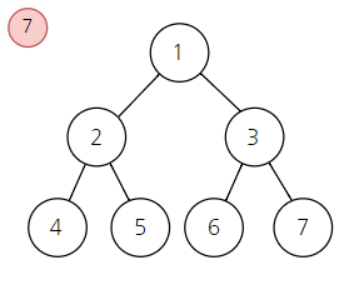
데이터가 첫 인덱스(루트) 노드부터 자식노드가 왼쪽, 오른쪽으로 차근차근 들어가는 구조. 즉 ,중간에 비어있는 곳 x
정렬
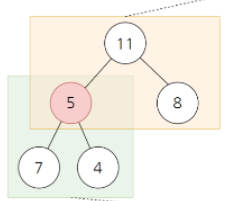
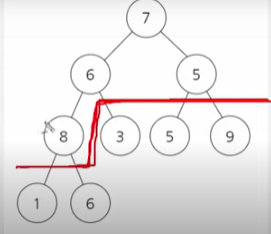
트리에서 최대 힙을 만족하고 싶지만 그렇지 않을 경우(위 사진처럼) 힙 정렬 수행 => 힙 생성 알고리즘을 사용
힙생성 알고리즘
- 특정한 노드의 두 자식 중에서 더 큰 자식과 자신의 위치를 바꾸는 알고리즘 = 최대힙
- 힙 생성 알고리즘은 특정한 하나의 노드에 대해서 수행
- 하나의 노드를 제외하고는 최대 힙이 구성되어 있는 상태 (위 사진처럼)
- 특정 노드가 아닌 데이터를 정렬하려면 전체 개수 / 2 의 내림수 만큼만 힙 생성알고리즘 적용하면 됨. ( 전체 개수 / 2 의 내림수 부터는 모두 마지막 자식들 - 아래 사진 처럼)
출처 : 동빈나 블로그
PYTHON heapq 모듈
- min heap을 사용하면 원소들이 항상 정렬된 상태로 추가되고 삭제
- 최소힙 구조
- 내부적으로 min heap 내의 모든 원소(k)는 항상 자식 원소들(2k+1, 2k+2) 보다 크기가 작거나 같도록 원소가 추가되고 삭제
모듈 임포트
▶ import heapq
기존 리스트를 힙으로 변환
▶ heapq.heapify(리스트)
최소 힙 생성
▶ 리스트와 별개의 자료구조가 아님.
▶ 따라서 heapq 모듈의 함수를 호출할 때 마다 이 리스트를 인자로 넘겨야함.
▶ 힙 생성할 거면 그냥 빈 리스트 생성하면 됨.
▶ 파이썬에서는 heapq 모듈을 통해서 원소를 추가하거나 삭제한 리스트가 그냥 최소 힙
힙에서 원소 추가
▶heapq.heappush(리스트, 넣을 값)
- 내부적으로 이진 트리에 원소를 정렬하며 추가
힙에서 원소 삭제
▶ heapq.heappop(리스트)
- 원소를 삭제할 대상 리스트를 인자로 넘기면, 가장 작은 원소를 삭제 후 리턴
최소값 삭제하지 않고 얻기
▶ print(heap[0])
-
힙의 구조상 인덱스 1에 두번째로 작은 원소가 있다는 것은 아니다.
-
따라서 두번째로 작은 원소를 얻으려 heappop()을 통해 가장 작은 원소를 삭제 후, heap[0]를 통해 새로운 최소값에 접근. (heap[1] x)
