❓ 다이나믹 프로그래밍(DP)이란?

큰 문제를 작은 문제로 쪼개어 작은 문제들을 해결, 저장 하여 큰 문제를 해결한다.
즉, 한번 푼 문제는 다시 풀지 않음
-> 메모이제이션(memoization) : 계산한 결과는 배열에 저장.

❓ 언제 사용할까?

1. 특정 조건을 충족하기 위해 시퀀스에서 요소를 재배열하는 방법의 수
2. 한 정접에서 다른 정점으로의 경로 수같은 것을 계산할 때
   ㄴ 특정 값이나 수량을 최적화
3. 무언가 가능한지 확인
   ㄴ ex) 주어진 숫자 집합이 대상 값과 정확히 동일한 요소의 합을 가진 하위 집합이 있는지 확인

   greedy가 작동하지 않는 상황이면 일반적으로 DP가 올바른 방법
   
   

❗ 반복과 재귀의 차이

반복	재귀
일반적으로 서로 내포된 몇개의 for 루프를 작성	순진한 솔루션이나 역추적 구현, 다음 메모제이션 추가 -> 쉬움
속도	쉬운 접근
오버헤드 작-> 실행시간 작	단일 문제에서 방문할 스테이트 수가 더 적음
쉬운 복잡도	상태의 순서 중요하지 않음
어려운 기술 구현가능

❗ 다이나믹 프로그래밍(DP) 사용조건

1) 동일한 작은 문제들이 반복하여 나타나는 경우에 사용한다. ( = 큰 문제를 중복되는 작은 문제로 쪼갤 수 있다.)
2) 작은 문제에서 구한 결과로 그것을 포함하는 큰 문제에서 활용하여 전체 결과를 낼 수 있다.

! 분할 정복과 DP는 큰 문제를 작게 쪼갠 문제들을 해결하고 연계적으로 큰 문제를 해결하는 것은 같음. 하지만 분할 정복은 쪼개진 작은 문제가 반복이 아닐때 사용하므로 DP와의 차이점을 가짐.

다이나믹 프로그래밍(DP) 사용순서

1) DP문제인지 확인
2) 문제의 변수 파악
3) 변수 간 관계식 만들기(점화식)
4) memoization
5) 초기값 확인하기(기저 상태 파악)
6) 구현

ex) 피보나치 수열
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 ...

==> 재귀 (피보나치 수열 점화식) return f(n) = f(n-1) + f(n-2)

출처

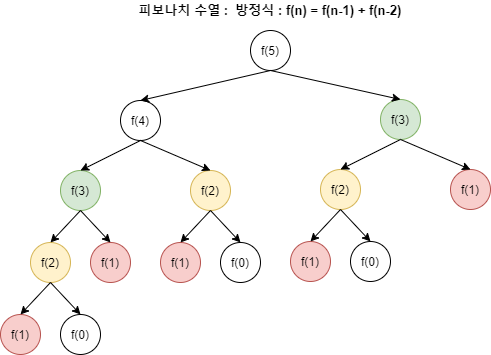
위 그림처럼 똑같은 값을 또 계산하여 연산이 기하급수적으로 늘어남. -> 비효율

==> DP사용
🔷프로그래머스 피보나치 수 문제
🔷하노이의 탑

이전 값(작은 문제의 결과)를 이용하여 큰 문제의 값을 도출

def solution(n):
    li = [0,1]

    for i in range(n-1):
        answer = li[0] + li[1]
        if i%2 == 0 : li[0] = answer
        else : li[1] = answer
    return answer % 1234567

참고