문제 설명
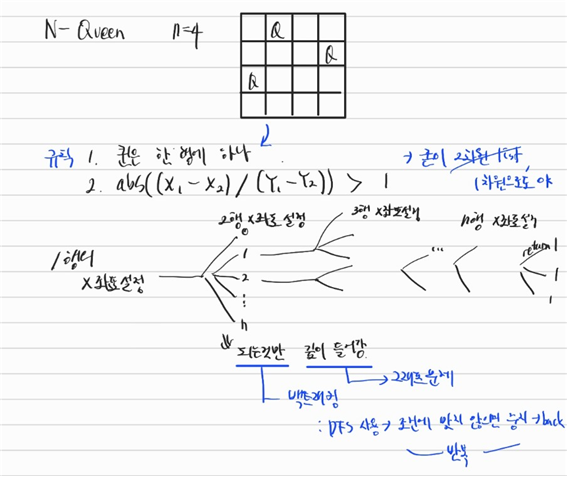
가로, 세로 길이가 n인 정사각형으로된 체스판이 있습니다. 체스판 위의 n개의 퀸이 서로를 공격할 수 없도록 배치하고 싶습니다.
예를 들어서 n이 4인경우 다음과 같이 퀸을 배치하면 n개의 퀸은 서로를 한번에 공격 할 수 없습니다.
체스판의 가로 세로의 세로의 길이 n이 매개변수로 주어질 때, n개의 퀸이 조건에 만족 하도록 배치할 수 있는 방법의 수를 return하는 solution함수를 완성해주세요.
풀이 & comment
최근에 그래프, 재귀 문제가 술술 풀려서 이런 문제에 도가 텄는 줄 알았는데 역시는 역시였다.
대충 머릿속에 그려지는 대로 코드를 작성했더니 여기저기서 오류가 났으며 제대로된 순서를 확실하게 잡아놓고 시작하지 않아 헷갈려서 시간이 많이 걸렸다.
-> 결국 다른사람 풀이 보기 ㅎ,..
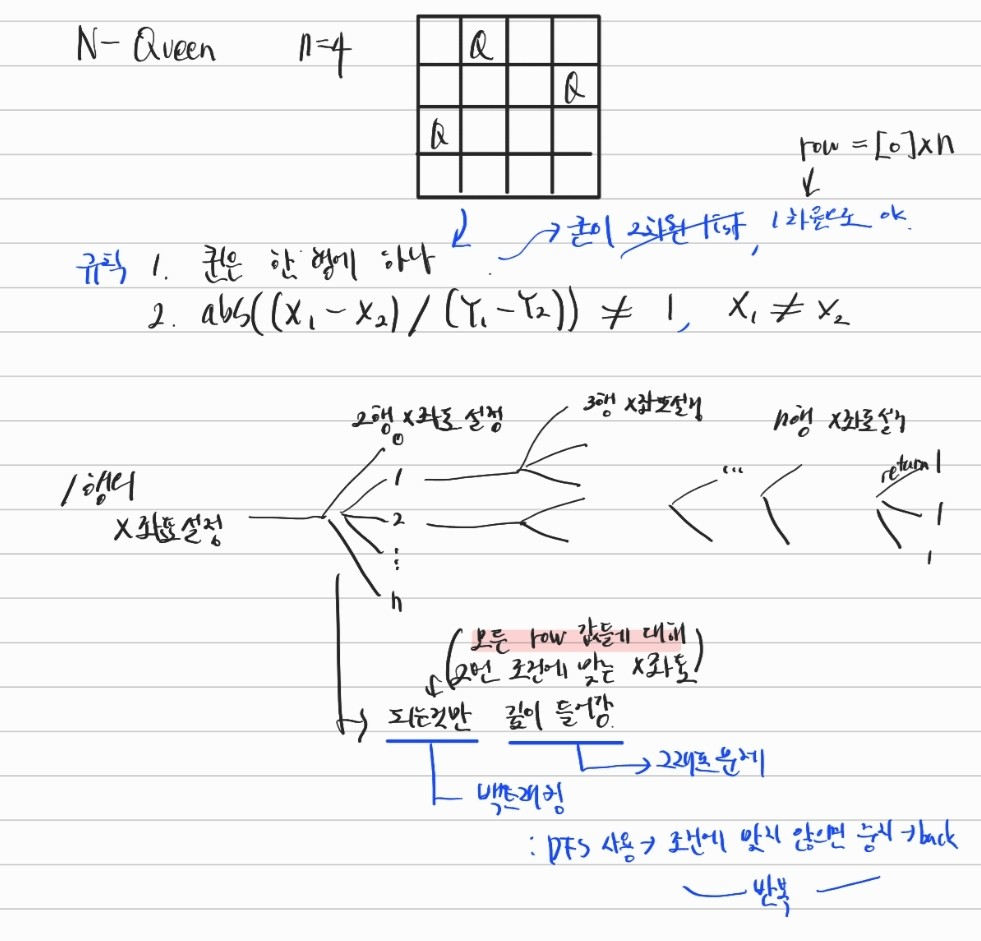
처음엔 좌표로 coord[(x,y) ..] 이렇게 저장하려했는데 1차원 리스트로 각 인덱스가 y좌표, 값을 x좌표로 사용하는 것을 보고 구현하니 훨씬 헷갈리지않고 쉬웠다.
위 이미지처럼 처음부터 순서, 전체적인 배경을 잡고 들어갔으면 시간이 얼마 안걸렸을텐데 이게 아직까지는 쉽지않다 ^8^

한번 풀었던 것 다시 풀었는데 사람 심리가 과거의 풀었으니까 얕잡아 보게되는 조굼이라도 막히면 과거의 풀이를 보게되는 결국 과거의 내풀이를 빼껴쓰게되버린 ^9^ 나중에 다시 풀어야되는 상황이 ^8^
2022.10.02
내 힘으로 지짜지짜 풀어봐야지 -> 2시간만에 기절
결국 또 이전 코드 봄 = 유정이는 발전이 없다.
먼 미래에 다시 찾아와야겠다.
코드
def solution(n):
answer = 0
row = [0] * n
def Queen(y):
nonlocal answer
if y == n:
answer +=1
return
else:
for i in range(n):
row[y] = i
# 넣어서 되는지 확인
for j in range(y):
if row[y] == row[j] or abs((row[y] - row[j]) / (y - j)) == 1:
break
else:
Queen(y+1)
Queen(0)
return answer거진 과거의 풀이 뺏김
def solution(n):
answer = 0
board = [0 for i in range(n)]
def Queen(count):
nonlocal answer
if count == n:
answer += 1
return
else:
for x in range(n):
board[count] = x
for y in range(count):
if board[y] == x or abs((x-board[y])/(count-y)) == 1:
break
else: Queen(count+1)
Queen(0)
return answer